例1.给定带权有向图(如下图所示),G=(V,E),其中每条边的权是非负实数。另外,还给定V中的一个顶点,称为源,本题以顶点1为源。现在要计算从源到所有其它各顶点的最短路长度。这里路的长度是指路上各边权之和。现采用Dijkstra算法计算从源顶点1到其它顶点间最短路径。请将此过程填入下表中。

|
迭代 |
S |
U |
Dist[2] |
Dist[3] |
Dist[4] |
Diast[5] |
|
初始 |
{1} |
|||||
|
1 |
||||||
|
2 |
||||||
|
3 |
||||||
|
4 |
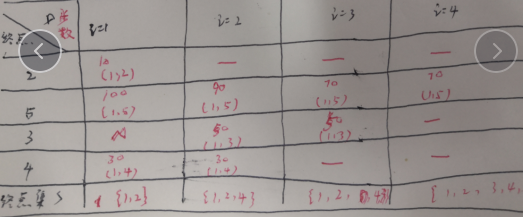
|
迭代 |
S |
U |
Dist[2] |
Dist[3] |
Dist[4] |
Dist[5] |
|
初始 |
{1} |
- |
10 |
30 |
100 |
|
|
1 |
{1,2} |
2 |
10 |
60 |
30 |
100 |
|
2 |
{1,2,4} |
4 |
10 |
50 |
30 |
90 |
|
3 |
{1,2,4,3} |
3 |
10 |
50 |
30 |
70 |
|
4 |
{1,2,4,3,5} |
5 |
10 |
50 |
30 |
70 |
例2:快速排序的基本思想是:在待排序的n个元素中任取一个元素(通常取第一个元素)作为基准,把该元素放入最终位置后,整个数据序列被基准分割成两个子序列,所有小于基准的元素放置在前子序列中,所有大于基准的元素放置在后子序列中,并把基准排在这两个子序列的中间,这个过程称作划分。划分算法如下:
int Partition(int a[],int s,int t)//划分算法,返回划分好以后基准元素的位置。a是待排序列,s是待排序列的开始下标,t是待排序列的结束下标。
{ int i=s,j=t;
int tmp=a[s]; //用序列的第1个记录作为基准
while (i!=j) //从序列两端交替向中间扫描,直至i=j为止
{ while (j>i && a[j]>=tmp)
j- -; //从右向左扫描,找第1个关键字小于tmp的a[j]
a[i]=a[j]; //将a[j]前移到a[i]的位置
while (i<j && a[i]<=tmp)
i++; //从左向右扫描,找第1个关键字大于tmp的a[i]
a[j]=a[i]; //将a[i]后移到a[j]的位置
}
a[i]=tmp;
return i;
}
设待排序列为:7,8,6,4,10,3,9,5。起始下标为0,结束下标为7。请写出第一次调用该算法后的序列和基准元素所处的位置(下标值)。
五、算法设计
要求对教材中所有例子和所布置的作业,能结合设计好的数据结构,构造算法,举例如下:
例.多机调度问题:设有n个独立的作业{1,2,…,n},由m台相同的机器{1,2, …,m}进行加工处理,作业i所需的处理时间为ti(1≤i≤n),每个作业均可在任何一台机器上加工处理,但未完工前不允许中断,任何作业也不能拆分成更小的子作业。利用贪心算法来解决该问题。定义以下数据结构。
#define M 20 //最多的机器台数
#define N 10 //最多的作业数
typedef struct { //采用结构体存放一个作业
int w; //作业编号
int t; //作业的处理时间
}Work; //Work是作业类型,该类型数据用来保存一个作业
typedef struct { //采用结构体存放一个作业
Work seq[N]; //机器的作业序列
int num; //机器处理的作业总数
int sumt; //机器总处理时间
}PlanType; //调度分配方案类型
假设每一个作业已经按照处理时间降序排列,则可采取如下贪心算法求解调度方案。
void Mscheduling(Work w[],int n,PlanType S[],int m)
//求n个作业w[0..n]在m台机器s[0..m]上的调度方案。
{ int i,j,k;
//i用来控制作业的分配,j用来保存已使用机器中处理时间最小的机器下标,k用来控制机器下标的变化。
for(i=0;i<m;i++) //将m个作业分配给m台机器
{ S[i].num=S[i].sumt=0;
S[i].seq[S[i].num]=w[i]; //将作业P[i]分配给机器i
S[i].sumt=w[i].t; //累加处理时间
}
//分配余下的作业
//求所有机器中处理时间总数最小的下标j
//将作业P[i]分配给机器j
//累加处理时间
//累计处理作业数
}
}