递归——习题

1、什么是直接递归和间接递归

直接递归：一个函数或过程调用了自身

间接递归：过程或函数p调用过程或函数q，而过程或函数q又调用p。

2、消除递归一般要用到什么数据结构

栈数据结构

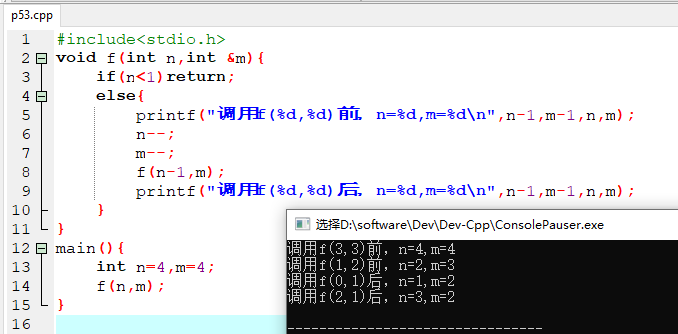
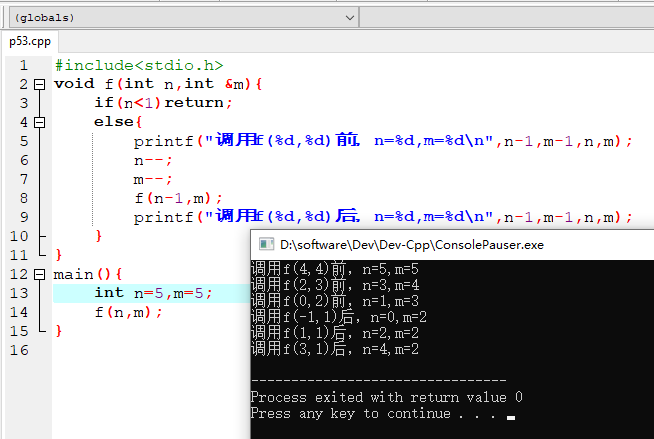
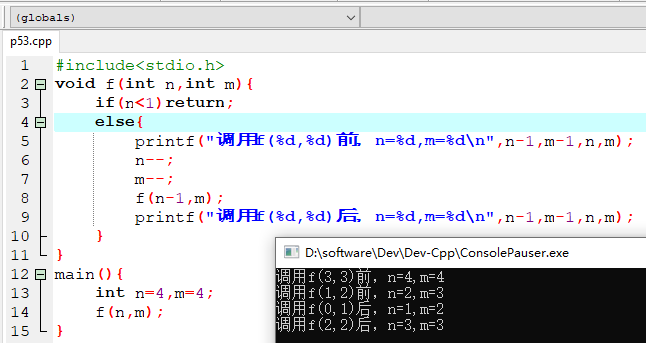
3、分析程序的执行过程

#include<stdio.h>
void f(int n,int &m){
    if(n<1)return;
    else{
        printf("调用f(%d,%d)前，n=%d,m=%d
",n-1,m-1,n,m);
        n--;
        m--;
        f(n-1,m);
        printf("调用f(%d,%d)后，n=%d,m=%d
",n-1,m-1,n,m);
    }
} 
main(){
    int n=4,m=4;
    f(n,m);
}

 

 4、某递归算法的执行时间T(n)有以下递归关系：

T（1）=1

T  (n)=T(n/3)+T(2n/3)+n   当n>1

 5、采用直接推导的方法求解以下递归问题：

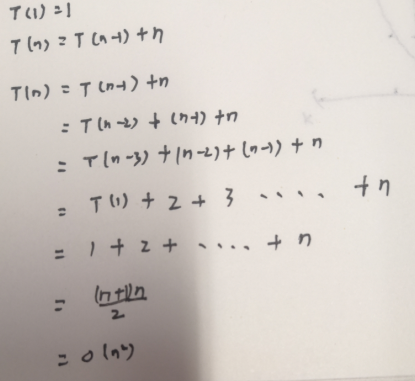
 通过以上两个求时间复杂度的问题，可以看出对于有两个分支的表达式要用递归树来求解，一个分支的可以直接化简即可。

6、不带头结点的单链表L，递归算法逆序输出：

#include<stdio.h> 
typedf struct Lnode{//存储结构 
int date;
struct Lnode *next;
}Node;

void disp(Node *L){
    if(L!=null)
    disp(L->next);
    printf("%d",L->date);
}

7、不带头结点的单链表L，递归算法删除第一个值为x的结点：

void Del_X(LinkList &L,ElemType x)
{
    LNode *p;
    if(L==NULL)
        return ;
    if(L->data==x)//找到了 
    {
        p=L;
        free(p);

    }else//没找到 
    {
        Del_X(L->next,x);
    }
}

8、假设二叉树采用二叉链存储结构，所有结点的值都不相同，设计递归算法求值为x的结点的层次（根结点层次为1）：

int Level(BTNode *bt,int h,int x) {//初始值 h=1 
    if(bt == NULL)
        return 0;
    if(bt->data == x )
        return h;
    else {
        int lh = Level(bt -> lchild,h+1 ,x);  // 在左子树中查找
        if(lh != 0)  // 在左子树中找到，返回其层次 
            return lh;
        else//在左子树没查找到 
            return Level(bt -> rchild, h+1 ,x);  // 返回在右子树的查找结果
    }
}

9、假设二叉树采用二叉链结构存放，设计递归算法由二叉树b复制产生二叉树t

typedef struct node{
    int data;
    struct node *lchild,*rchild;
}BTnode;

BTnode copy(BTnode *b){
    Btnode *newnode;
    if(b==null)
    return null;
    else{
        newnode=(BTnode*)malloc(sizeof(BTnode));
        newnode->data=b->data;
        newnode->lchild=copy(b->lchild);
        newnode->rchild=copy(b->rchild);
        return newnode;
    }
}