基本问题
输入:二维数组num[][],假设二维数组为m行n列
输出:二维数组中最大子数组的和
解法与思路:
1、O(m3n3)算法
即直接对所有子数组进行遍历,并记录最大和。遍历方法:穷举所有子数组的左上角坐标(i,j)和右下角坐标(x,y),然后计算该子数组的和,并保留较大解。由于穷举的子数组个数为O(m2n2),计算子数组和的复杂度为O(mn),所以算法整体复杂度为O(m3n3)
具体代码如下所示:
1 def maxsum_m3n3(m, n): 2 maxsofar = 0 3 for i in range(m): 4 for j in range(n): 5 for x in range(i, m): 6 for y in range(j, n): 7 sumnow = 0 8 for a in range(i, x+1): 9 for b in range(j, y+1): 10 sumnow += num[a][b] 11 if sumnow > maxsofar: 12 maxsofar = sumnow 13 return maxsofar
2、O(m2n2)算法
可以看到,上述算法可分为两部分:穷举子数组和计算子数组的和,本算法考虑对计算子数组的和进行优化,使用数组预处理来使计算子数组和的复杂度降为O(1)。预处理得到数组presum,presum[i][j]表示左上角坐标(1,1)、右下角坐标(i,j)的子数组的和。这样在计算子数组的和时,便可利用presum[][]的存储结果,左上角坐标(i,j)、右下角坐标(x,y)的子数组的和等于presum[x][y] - presum[x][j-1] - presum[i-1][y] + presum[i-1][j-1]。这是算法复杂度降低为穷举子数组的个数,所以复杂度为O(m2n2)
具体代码如下所示(需确保数组下标不为-1):
1 def maxsum_m2n2(m, n): 2 maxsofar = 0 3 4 presum = [[0 for col in range(n)] for row in range(m)] 5 #数组预处理 6 for i in range(m): 7 for j in range(n): 8 if i == 0 and j == 0: 9 presum[i][j] = num[i][j] 10 elif i == 0: 11 presum[i][j] = presum[i][j-1] + num[i][j] 12 elif j == 0: 13 presum[i][j] = presum[i-1][j] + num[i][j] 14 else: 15 presum[i][j] = presum[i-1][j] + presum[i][j-1] - presum[i-1][j-1] + num[i][j] 16 17 #求解 18 for i in range(m): 19 for j in range(n): 20 for x in range(i, m): 21 for y in range(j, n): 22 if i == 0 and j == 0: 23 sumnow = presum[x][y] 24 elif i == 0: 25 sumnow = presum[x][y] - presum[x][j-1] 26 elif j == 0: 27 sumnow = presum[x][y] - presum[i-1][y] 28 else: 29 sumnow = presum[x][y] - presum[x][j-1] - presum[i-1][y] + presum[i-1][j-1] 30 maxsofar = max(maxsofar, sumnow) 31 32 return maxsofar
3、O(m2n)算法
考虑如何利用一维数组求最大和的O(n)算法。可以对二维数组的多行进行压缩,变二维为一维,然后再调用一维的O(n)算法。将左上角坐标为(a,1)、右下角坐标为(c,n)的数组压缩为一维数组com[],一维数组长度为n。为了可以快速实现压缩,引入预处理数组presum[][],presum[i][j]等于num[0][j]+num[1][j]+...+num[i][j],即第j列从1行到i行的和,这样com[j]=presum[c][j]-presum[a][j]。穷举所有可以压缩的二维数组的复杂度为O(m2),调用一维算法的复杂度为O(n),所以算法的整体复杂度为O(m2n)
具体代码如下:
1 def maxsum_m2n(m, n): 2 maxsofar = 0 3 4 presum = [[0 for col in range(n)] for row in range(m)] 5 #预处理 6 for i in range(m): 7 for j in range(n): 8 if i == 0: 9 presum[i][j] = num[i][j] 10 else: 11 presum[i][j] = presum[i-1][j] + num[i][j] 12 13 #求解 14 com = [0 for col in range(n)] 15 for a in range(m): 16 for c in range(a, m): 17 for i in range(n): 18 if a == 0: 19 com[i] = presum[c][i] 20 else: 21 com[i] = presum[c][i] - presum[a-1][i] 22 #print max_subseq(com) 23 maxsofar = max(maxsofar, max_subseq(com)) 24 25 return maxsofar
衍生问题
1、假设数组是在水平方向首尾相连的,此时的二维数组如何求解
解法:将数组有m行n列扩展为m行2n列,在穷举左上角坐标(i,j)、右下角坐标(x,y)的子数组时保证列号的差y-j小于n即可
2、假设数组是在垂直方向首尾相连的,此时的二维数组如何求解
解法:将数组有m行n列扩展为2m行n列,在穷举左上角坐标(i,j)、右下角坐标(x,y)的子数组时保证行号的差x-i小于m即可
3、子数组的定义改为连通子数组,即元素相互连通则称为连通子数组,如何求解最大连通子数组
解法:有待继续思考。。。
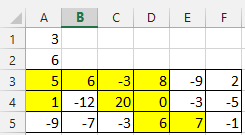
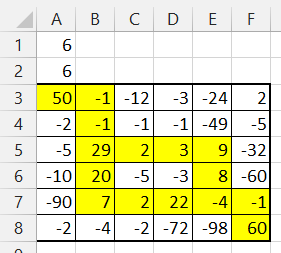
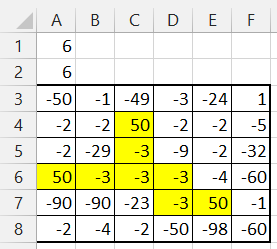
下面贴几个连通子数组的测试用例(来自http://www.cnblogs.com/xinz/p/3318230.html)