今年做了现代程序设计课的助教,邹老师第一节课为了考察学生编程水平,就留了下面这道题作为课堂作业,为了当好助教,在此稍作总结
问题:求解一维数组中的任何连续子数组的和的最大值,此题是各种面试、算法课中的经典问题,本文将对目前遇到的各种解法做个实践与归纳
输入:长度为n的数组num[0...n-1]
输出:连续子数组和的最大值
解法与思路:
1、O(n3)解法
考虑数组num[]的子数组个数,对于子数组num[i...j],其中0≤i≤j<n,子数组共有n+n-1+n-2+...+2+1=n(n+1)/2个。对于每个子数组再求和,并记录其最大值,子数组的平均长度为O(n),所以算法复杂度为O(n3),具体的代码实现max_subseq_n3.py如下所示
1 #!/usr/bin/python 2 3 ''' 4 便于实验,在num.txt中每行一个[-10000,10000]的随机整数,共10000个 5 ''' 6 f = open("num.txt", "r") 7 num = [] 8 for line in f.readlines(): 9 num.append(int(line)) 10 11 n = len(num) 12 max_so_far = min(num) 13 14 for i in range(0, n): 15 for j in range(i, n): 16 sum = 0 17 for k in range(i, j + 1): 18 sum += num[k] 19 max_so_far = max(sum, max_so_far) 20 21 print max_so_far
使用time ./max_subseq_n3.py进行计时,得到结果如下(这个时间太长,明天再贴了。。。):
2、O(n2)解法
注意到sum(num[i...j]) = sum(num[i...j-1]) + num[j],可以在计算子数组num[i...j]的和时利用上一个子数组num[i...j-1]的结果,这样便可减少子数组和的计算,使算法减少一层循环,时间复杂度降低到O(n2),具体的代码实现max_subseq_n2.py如下所示
1 #!/usr/bin/python 2 3 f = open("num.txt", "r") 4 num = [] 5 for line in f.readlines(): 6 num.append(int(line)) 7 8 n = len(num) 9 max_so_far = min(num) 10 11 for i in range(0, n): 12 sum = 0 13 for j in range(i, n): 14 sum = sum + num[j] 15 max_so_far = max(sum, max_so_far) 16 17 print max_so_far
使用time ./max_subseq_n2.py进行计时,得到结果如下:

3、O(nlogn)解法
使用分治法,要解决规模为n的问题,可以递归的解决两个规模近为n/2的子问题,然后对它们的答案进行合并以得到整个问题的答案。将数组num[0...n-1]划分为两个大小近似为n/2的子数组a和b

然后递归的找出数组a和b的最大子数组的和为ma和mb

合并子问题的答案时可以发现,原问题的最大子数组也可能跨越a和b的边界,设其和为mc

所以可得原问题的解为max(ma, mb, mc),具体的代码实现max_subseq_nlogn.py如下所示
1 #!/usr/bin/python 2 3 f = open("num.txt", "r") 4 num = [] 5 for line in f.readlines(): 6 num.append(int(line)) 7 n = len(num) 8 9 def maxsum(start, end): 10 if start > end: 11 return 0 12 if start == end: 13 return max(0, num[start]) 14 mid = (start + end) / 2 15 smax = sum = 0 16 for i in range(mid, -1, -1): 17 sum += num[i] 18 smax = max(smax, sum) 19 emax = sum = 0 20 for i in range(mid + 1, end): 21 sum += num[i] 22 emax = max(emax, sum) 23 return max(smax + emax, maxsum(start, mid), maxsum(mid + 1, end)) 24 25 print maxsum(0, n-1)
使用time ./max_subseq_nlogn.py进行计时,得到结果如下:
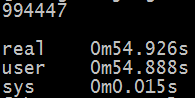
4、O(n)解法
从数组下标0开始扫描至到i,假设已经知道num[0...i-1]的最大子数组的和为max_so_far,那么此时在有了下标i后,最大子数组要么包含num[i]并以num[i]结尾,要么不包含num[i],假设以num[i]结尾的最大子数组的和为max_ending_here,则max_so_far = max(max_so_far, max_ending_here)。此时,问题转换为如何求解max_ending_here
可以知道在扫描num[i]前已经知道了num[0...i-1]的已num[i-1]结尾的最大子数组的和为max_ending_here,则在扫描num[i]后,max_ending_here将变为以num[i]结尾的最大子数组的和,所以max_ending_here = max(max_ending_here + num[i], num[i]),这样再根据上式便可以求解出max_so_far

具体的代码实现max_subseq_n.py如下所示
1 #!/usr/bin/python 2 3 f = open("num.txt", "r") 4 num = [] 5 for line in f.readlines(): 6 num.append(int(line)) 7 8 n = len(num) 9 max_so_far = 0 10 max_ending_here = 0 11 if max(num) < 0 12 max_so_far = min(num) 13 max_ending_here = min(num) 14 15 for i in range(0, n): 16 max_ending_here = max(max_ending_here + num[i], num[i]) 17 max_so_far = max(max_so_far, max_ending_here) 18 19 print max_so_far
注意:max_so_far和max_ending_here应初始化为0,但当全部元素小于0时,应初始化为数组最小值
使用time ./max_subseq_n.py进行计时,得到结果如下:
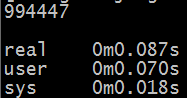
总结,根据上面的运行时间统计,就可以看出算法时间复杂度的影响了,当然这里的时间包含了读入num.txt的时间,算法真实运行时间并未实测,有兴趣的同学可以尝试一下
思考:max_so_far和max_ending_here初始化为数组中元素的最大值,岂不更好~~