Educational Codeforces Round 48

C. Vasya And The Mushrooms

题解：拿笔画他的行走路线，你会发现可以前缀和预处理一些东西出来。

const int N = 300005;

int n;
ll a[N], b[N], dp[2][N], sp[2][N], sum[N];

int get_a() {

    dp[0][0] = 0;
    for (int i = 1; i < n; ++i) {
        dp[0][i] = dp[0][i - 1] + 1ll * i * a[i];
    }

    int t = n;
    dp[1][n - 1] = dp[0][n - 1] + 1ll * t * b[n - 1];

    for (int i = n - 2; ~i; --i) {
        t++;
        dp[1][i] = dp[1][i + 1] + 1ll * t * b[i];
    }
}

int get_b() {

    sp[1][0] = b[1];
    for (int i = 1; i < n; ++i) sp[1][i] = sp[1][i - 1] + 1ll * (i + 1) * b[i];

    int t = n + 1;
    sp[0][n - 1] = sp[1][n - 1] + 1ll * t * a[n - 1];

    for (int i = n - 2; ~i; --i) {
        t++;
        sp[0][i] = sp[0][i + 1] + 1ll * t * a[i];
    }
}

void Inite() {
    for (int i = n - 1; ~i; --i) sum[i] = sum[i + 1] + a[i] + b[i];
}

void solve() {
    ll ans = max(dp[1][0], sp[0][1]);
    int last = 0;
    ll tp = 0;
    for (int i = 0; i < n; ++i) {
        if(!last) {
            tp += 1ll * 2 * i * a[i] + 1ll * (2 * i + 1) * b[i];
            if(i + 1 != n) ans = max(ans, tp + 1ll * i * sum[i + 1] + sp[0][i + 1] - sp[1][i]);
        }
        else {
            tp += 1ll * 2 * i * b[i] + 1ll * (2 * i + 1) * a[i];
            if(i + 1 != n) ans = max(ans, tp + 1ll * (i + 1) * sum[i + 1] + dp[1][i + 1] - dp[0][i]);
        }
        last ^= 1;
    }
    printf("%I64d
", max(ans, tp));
}

 D. Vasya And The Matrix

题解：可以这么构造，除了第一行，第一列填上以外，其它的行和列都填0，所以主要是算map[1][1]改填几，或者填最后一行和最后一列。

 ans[n][m] = b[m] ^ (x ^ a[n]);

 E. Rest In The Shades

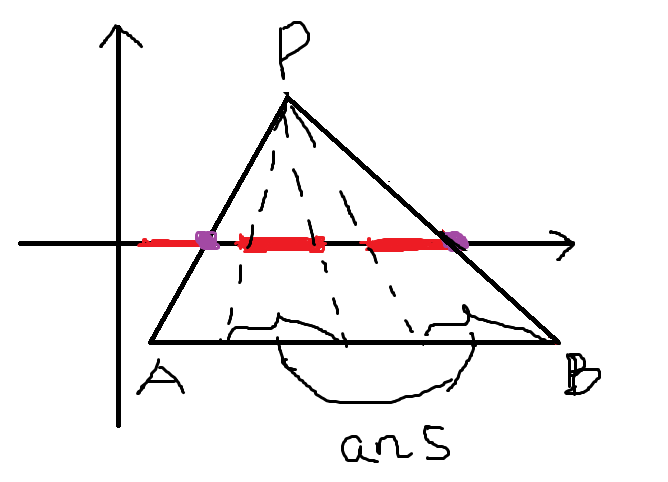
题解：假设一点为P点，那么P与灯的两端（A,  B）会构成一个三角形，先计算出PA与x轴的交点（图中紫色的点），PB与x轴的交点，然后再二分计算这两个交点之间fence的长度（红色线段的总长），最后利用相似三角形，算出这段长度在航线上的投影。做法是这样，就是为啥子能这么做，就要自己想了（P要被照亮，说明有光线能达到P点，所以反过来，从P点发出的光线，经过栅栏以后，在航线上呈现阴影的部分就是答案要求的部分）。

int sy, a, b, n, q;
double l[N], r[N], sum[N];

int main()
{
    sc(sy), sc(a), sc(b), sc(n);
    for (int i = 1; i <= n; ++i) {
        scanf("%lf %lf", &l[i], &r[i]);
        sum[i] = sum[i - 1] + r[i] - l[i];
    }
    sc(q);
    while(q--) {
        double x, y;
        scanf("%lf %lf", &x, &y);

        double xl = a + (x - a) * (-sy) * 1.0 / (y - sy);
        double xr = b + (x - b) * (-sy) * 1.0 / (y - sy);

        int idx = upper_bound(l+1,l+n+1,xl+1e-6)-l-1;
        int idy = upper_bound(l+1,l+n+1,xr+1e-6)-l-1;

        double er = idy > 0 ? (sum[idy - 1] + min(r[idy], xr) - l[idy]) : 0;
        double el = idx > 0 ? (sum[idx - 1] + min(r[idx], xl) - l[idx]) : 0;
        printf("%.8f
", (er - el) * (y - sy) / y);
    }
    return 0;
}

 F. Road Projects

PS：有个很重要的点，q个项目加边的位置是相同的，所以只需要找到加一条权值为0的边的位置。然而我并不知道怎么去找这个位置。。。待补