二叉树
-根节点
-左右叶子节点
-子树:
-不完整的子树
-完整的子树
- 结论:
- 一颗子数最少要包含一个根节点
- 一个完整的二叉树是由多个子树构成
- 一个子树的子节点也可以表示另一个子树的根节点
遍历
###遍历
-广度遍历:逐层遍历
-深度遍历:纵向遍历,前中后表示的是子树中根节点的位置
-一定要基于子树去遍历
-前序:根左右
-中序:左根右
-后序:左右根
为什么一定要有深度遍历呢?
-是因为深度遍历可以帮我们二叉树进行排序
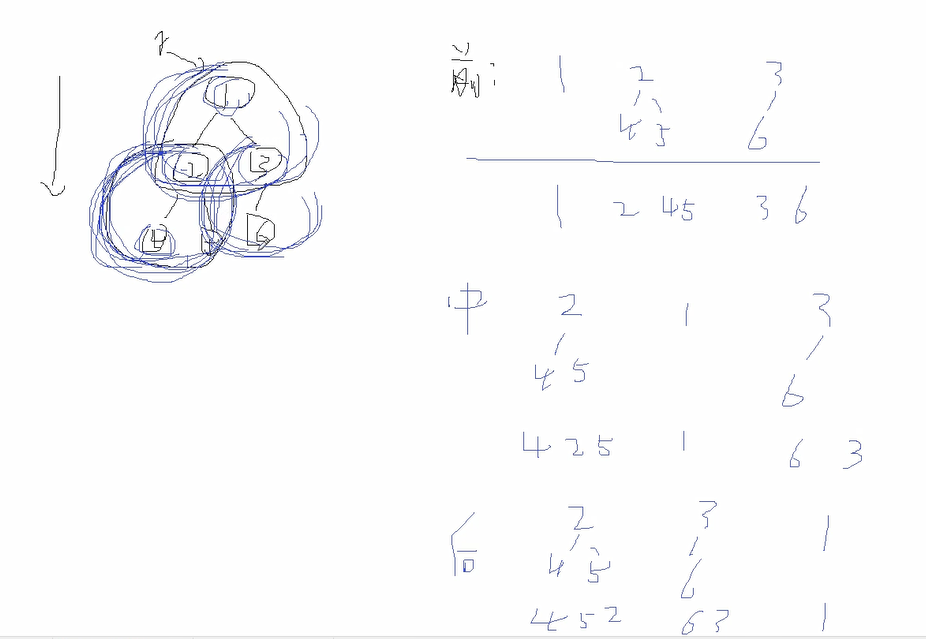
广度遍历/深度遍历
class Node(): #构造节点
def __init__(self, item): #构造方法
self.item = item #属性1
self.left = None #属性2
self.right = None #属性3
class Tree(): # 构建一个空树
def __init__(self):
self.root = None
def add(self, item): #添加
if self.root == None: # 向空树中插入第一个节点
node = Node(item)
self.root = node
return
# 向非空的二叉树中插入节点
node = Node(item)
cur = self.root
queue = [cur]
while queue:
root = queue.pop(0)
if root.left != None:
queue.append(root.left)
else:
root.left = node
break
if root.right != None:
queue.append(root.right)
else:
root.right = node
break
###广度遍历
def travel(self):
cur = self.root
queue = [cur]
if self.root == None:
print('')
return
while queue:
root = queue.pop(0)
print(root.item)
if root.left != None:
queue.append(root.left)
if root.right != None:
queue.append(root.right)
###深度遍历
def forward(self,root): #前序遍历 根左右 root(任意一颗子树的根节点)
if root == None:
return
print(root.item)
self.forward(root.left)
self.forward(root.right)
def middle(self,root): #中序遍历 左根右
if root == None:
return
self.middle(root.left)
print(root.item)
self.middle(root.right)
def back(self,root): #后序遍历 左右根
if root == None:
return
self.back(root.left)
self.back(root.right)
print(root.item)
tree = Tree()
tree.add(1)
tree.add(2)
tree.add(3)
tree.add(4)
tree.add(5)
tree.add(6)
# tree.travel()
tree.forward(tree.root)
tree.middle(tree.root)
tree.back(tree.root)
排序二叉树

class Node(): #构建节点
def __init__(self, item): #构造方法
self.item = item #属性1
self.left = None #属性2
self.right = None #属性3
class SortTree(): #构建空树
def __init__(self): #构造方法
self.root = None
def add(self, item):
node = Node(item)
cur = self.root
if self.root == None:
self.root = node
return
while True:
# 插入节点的值小于根节点的值:往根节点的左侧插
if node.item < cur.item:
if cur.left == None:
cur.left = node
break
else:
cur = cur.left
else: # 插入的节点的值大于跟节点:往根节点的右侧插
if cur.right == None:
cur.right = node
break
else:
cur = cur.right
def middle(self, root): #中序
if root == None:
return
self.middle(root.left)
print(root.item)
self.middle(root.right)
tree = SortTree()
alist = [3,8,5,7,6,2,1]
for i in alist:
tree.add(i)
tree.middle(tree.root)

