Fox Ciel has n boxes in her room. They have the same size and weight, but they might have different strength. The i-th box can hold at most xi boxes on its top (we'll call xi the strength of the box).
Since all the boxes have the same size, Ciel cannot put more than one box directly on the top of some box. For example, imagine Ciel has three boxes: the first has strength 2, the second has strength 1 and the third has strength 1. She cannot put the second and the third box simultaneously directly on the top of the first one. But she can put the second box directly on the top of the first one, and then the third box directly on the top of the second one. We will call such a construction of boxes a pile.

Fox Ciel wants to construct piles from all the boxes. Each pile will contain some boxes from top to bottom, and there cannot be more than xi boxes on the top of i-th box. What is the minimal number of piles she needs to construct?
The first line contains an integer n (1 ≤ n ≤ 100). The next line contains n integers x1, x2, ..., xn (0 ≤ xi ≤ 100).
Output a single integer — the minimal possible number of piles.
3 0 0 10
2
5 0 1 2 3 4
1
4 0 0 0 0
4
9 0 1 0 2 0 1 1 2 10
3
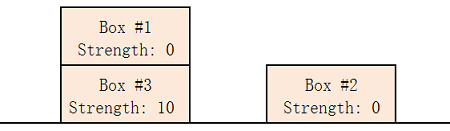
In example 1, one optimal way is to build 2 piles: the first pile contains boxes 1 and 3 (from top to bottom), the second pile contains only box 2.
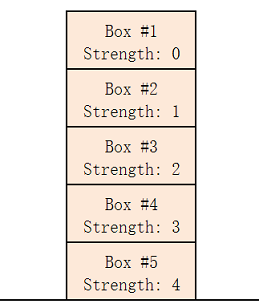
In example 2, we can build only 1 pile that contains boxes 1, 2, 3, 4, 5 (from top to bottom).
解题说明:模拟题,须要从上向下构造一个箱子堆,经过排序之后,首先保证最上面的都是最小的,其次是以下一层,直到最后遍历结束。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include <algorithm>
#include<cstring>
#include<string>
using namespace std;
int main()
{
int n, i, k, d[105];
k = 0;
cin >> n;
for (i = 0; i<n; i++)
{
cin >> d[i];
}
sort(d, d + n);
for (i = 0; i<n; i++)
{
if (k*(d[i] + 1) <= i)
{
k++;
}
}
cout << k << endl;
return 0;
}