P1 计算机早期历史-Early Computing

最早的计算设备--算盘,手动计算器,存储着当前的计算状态。

P2 电子计算机-Electronic Computing

最早的机电计算器之一,哈佛Mark 1号,这台机器的大脑是继电器。继电器里,有个控制线路,控制电路是开还是关,控制线路连着一个线圈,当电流通过线圈的时候,线圈产生电磁场,吸引金属臂,从而闭合电路。
但是继电器的机械臂有质量,因此无法快速的开关。除了速度慢之外,还会造成磨损,增加故障率。
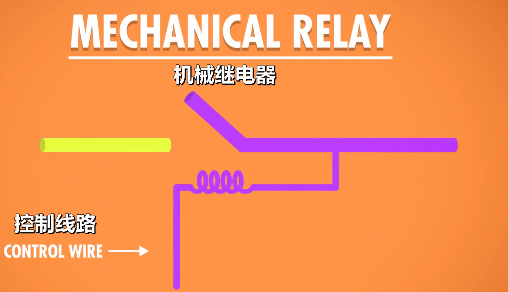
所以,想要进一步提高计算能力,需要更快更可靠的东西来代替继电器,即真空管。如下图,向控制电极施加正电荷,会允许电子流动,施加负电荷,会阻止电子的移动。所以通过控制电路,可以打开或关闭电路,和继电器的功能一样,但磨损更少,每秒可以开闭数千次。
这标志着计算机从机电转向电子。(electro-mechanical computing to electronic computing)



为了降低成本和大小,同时提高可靠性和速度,需要一种新的电子开关——晶体管。晶体管远远小于继电器和真空管,每秒能切换上百万次,并且能工作几十年。

从继电器---真空管--晶体管,让电路开闭的越来越快。
计算机采用二进制,多进制带来的问题是,状态越多,越难区分信号。
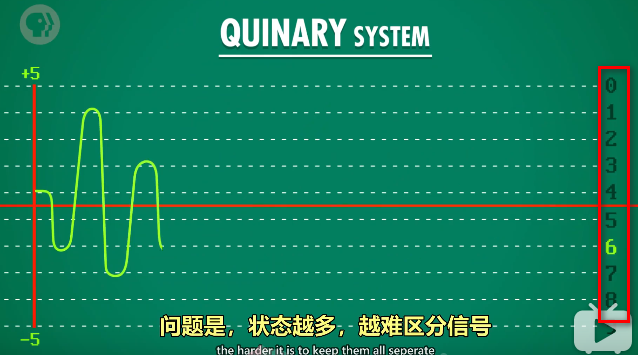
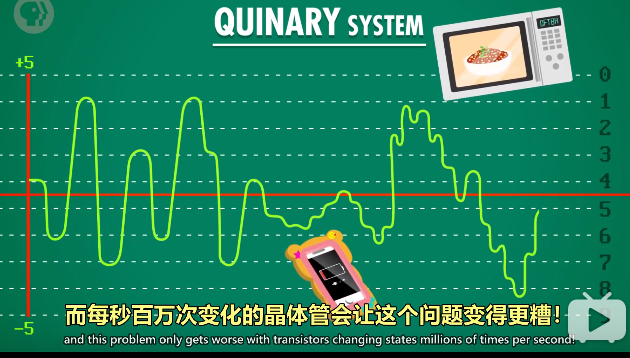
只用开和关两种状态,可以减少这类问题。
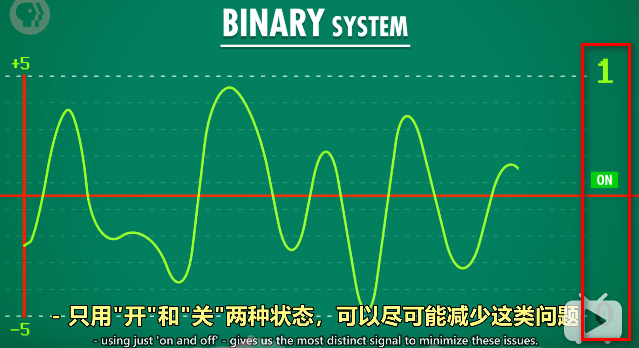
另一个使用二进制的原因是,有一整个数学分支,专门处理“真”和“假”,已经解决了所有法则和运算,即“布尔代数”。布尔代数中,变量的值不是数字,而是true和false,能进行逻辑操作。布尔代数中有三个基本操作,NOT、AND、OR,用晶体管可以实现。
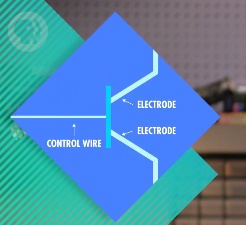
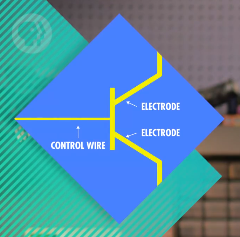
晶体管有三根线,2根电极和1根控制线,控制线通电时,电流就可以从一个电极流向另一个电极。将控制线当输入,底部电极用于输出,所以一个晶体管有一个输入和一个输出
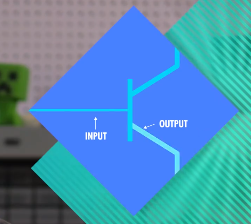
这样的话,打开输入,输出也会打开(输入为true,输出为true),关闭输入,输出也会关闭(输入为false,输出为false),对应的真值表:

实现NOT GATE:将输出放在上面那个电极,打开输入,电流流过接地,那么输出没有电流,即输入true,输出false。
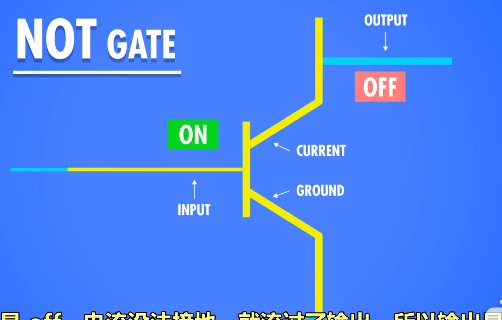
当输入是off,电流没法接地,就流过了输出,输出是on。
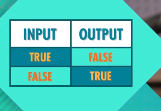
对应的NOT真值表
实现ADD GATE:将两个晶体管连接在一起,A和B都打开了,才会有输出。

对应的ADD真值表:

实现OR GATE:将两个晶体管并联起来,如下。
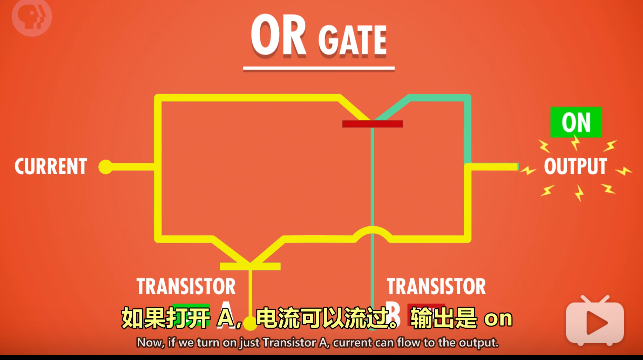
对应的OR真值表:

NOT门,AND门,OR门都可以用晶体管表示。抽象表示如下,可以用来构建更大的组件。



计算机如何存储和表示数字?
数字:位来表示(1和0 即true和false),1bytes = 8bits(0~255),32位计算机或64位计算机意味着是一块块处理数据,每块是32位或64位
字母:给字母编码,用数字来表示 ASCII--Unicode
所以,短信,YouTube视频,互联网上的网页,操作系统,只不过是一长串的1和0。


表示和存储数字是计算机的重要功能,但真正的目标是计算和有意义的处理数字。比如两个数字相加。这些操作由计算机中的“算术逻辑单元”(ALU)处理。ALU是计算机中负责运算的组件。

ALU有两个单元,算数单元和逻辑单元
算数单元:负责计算机里的所有数字操作,如半加器和全加器组成的加法器(由一大堆逻辑门巧妙的连接在一起)
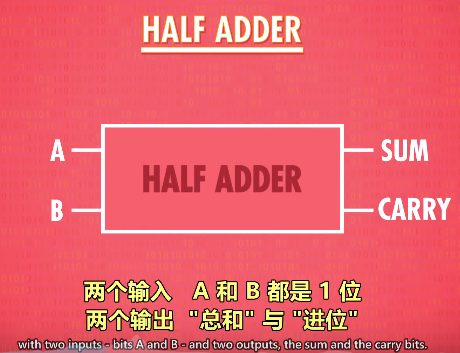
但想要处理超过1+1的运算,就需要全加器了。

有了半加器和全加器,利用他们来相加两个8位的数字。
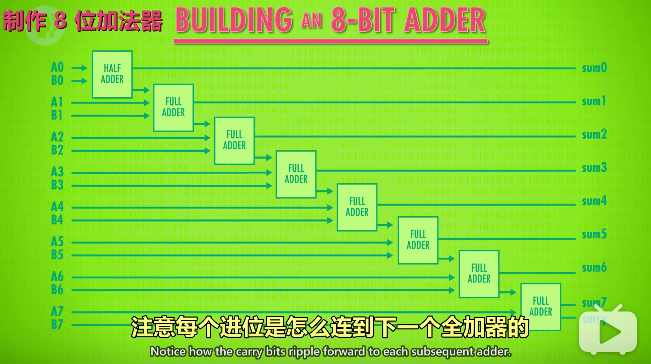
这样也可以得到16或32位加法器,但是需要更多的逻辑门,而这种方式每次进位都需要一点时间,而如今的计算器量级是每秒几十亿次运算,所以会造成影响。现代计算机用的加法电路有点不同,“超前进位加法器”。
逻辑单元:执行逻辑操作,ADD--OR--NOT等操作。
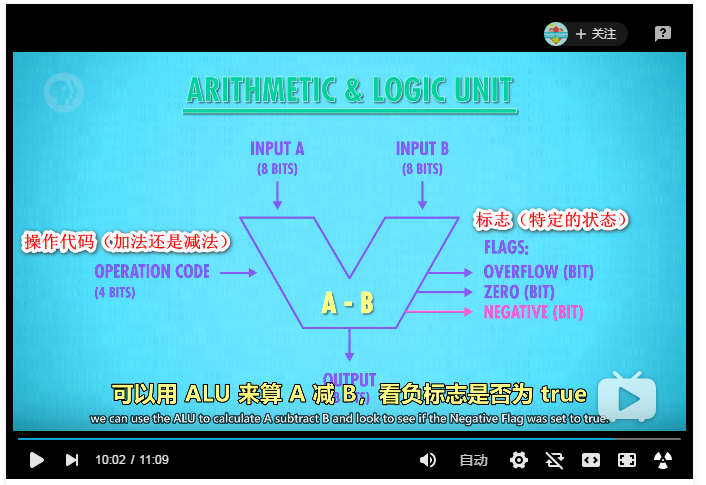
计算出之后如果扔掉了就没什么意义了,得找个办法存起来,这就用到了计算机内存了
ADD-OR锁存器实现存储1位的信息
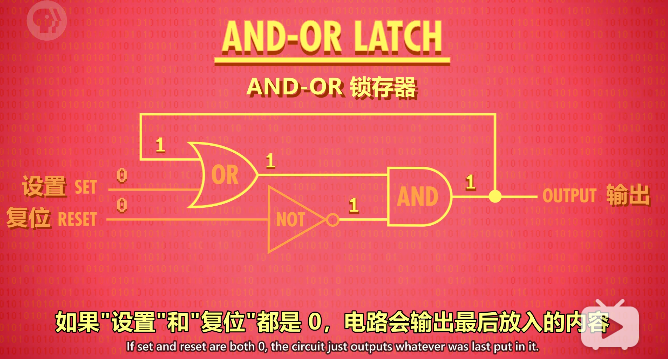
完善一下,将两个输入改成一个输入,添加一个允许写入线,得到门锁
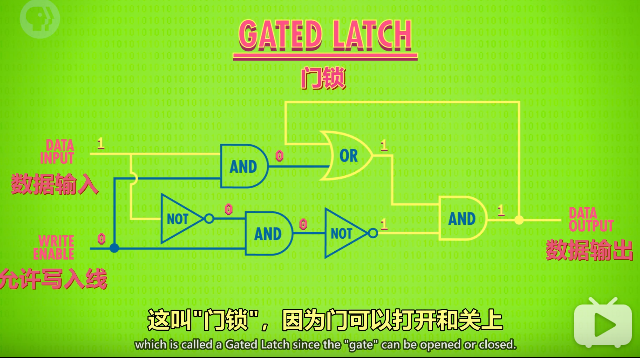
抽象一下,把门锁放到一个盒子里,这个盒子能够存储一个bit
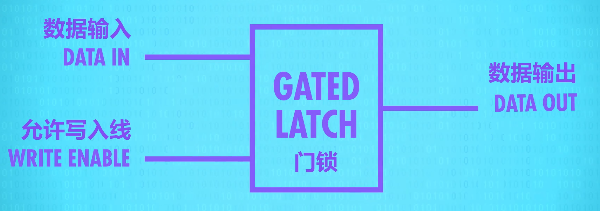
允许输入线输入1,打开门,数据输入1,1就可以保存在门锁中,数据输出是1,此时关闭允许写入线,无论数据输入是1还是0,门锁中保存的都是1,输出也永远都是1。
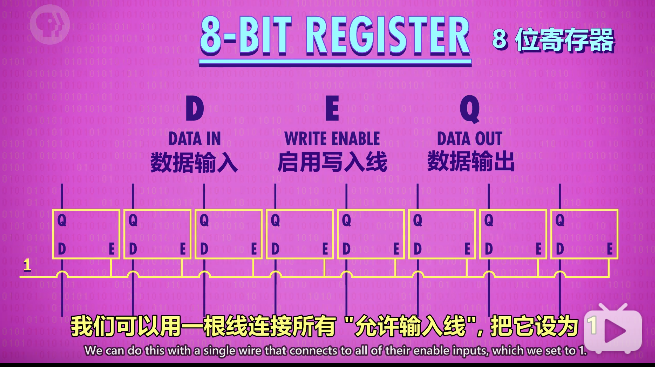
如果并排放8个锁存器,那就可以存8位信息,比如一个8bit的数据,一组这样的锁存器就叫做寄存器。

写入寄存器之前,要先启用里面所有的锁存器。用一根线连接所有的“允许输入线”,将之设置为1,允许写入
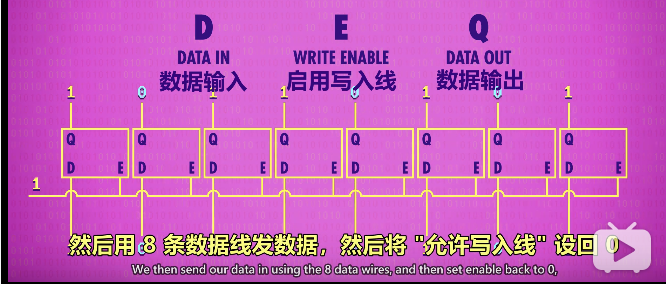
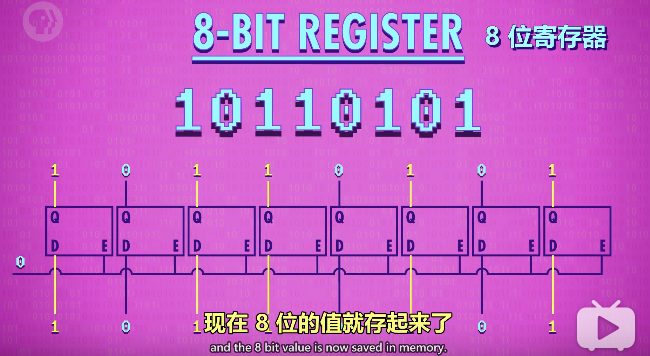
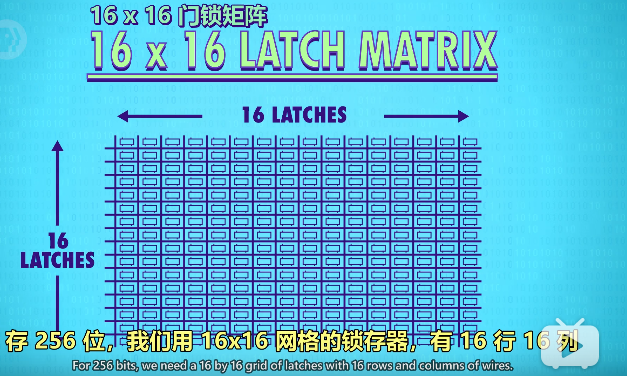
如果这样并排放置,以64位寄存器为例,需要64根数据线,64根连到输出端,一根线启用所有的锁存器,加起来需要64+64+1 = 129根线。就要存256位就需要256+256+1 = 513条线,这样线太多,解决方法就是矩阵。
在矩阵中,不是并列排放锁存器,而是做成网格

启用某个锁存器,就打开相应的行线和列线就好
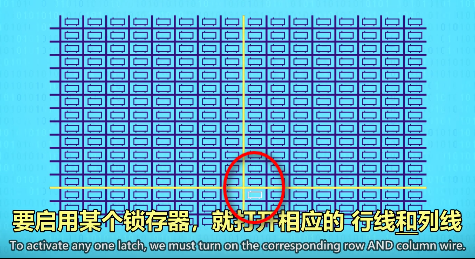
我们只想打开交叉处锁存器的允许写入线,所有其他的锁存器保持关闭。看下图,只有行线和列线均为1,ADD门才会输出1,用一根允许写入线连所有的锁存器,所以为了让该锁存器允许写入,行线和列线以及允许写入线都必须是1,每次只有一个锁存器会这样,这样就可以只用一个数据线来连接所有的锁存器来传输数据,因为只有一个锁存器会启用,只有那个会存数据,其他锁存器会忽略数据线上的值,因为没有允许写入。同样可以用类似的技巧,做允许读取线来读数据,从一个指定的锁存器中读取数据。
所以对于256位的存储,只需要1条数据线传输数据,1条允许写入线,1条允许读取线,还有16条行线+16条列线用于选择锁存器,即需要1+1+1+16+16 = 35条线。相比于并排排列的513条线,节省许多。

接下来就需要某种方法来唯一指定交叉点的地址,比如刚刚存了一位的地址是“12行8列”,由于最多只有16行(16列),所以可以用4bit来表示行数(列数),这样行地址(12)就可以表示成1100,列地址(8)表示成1000,即12行8列的地址就可以表示成11001000。计算机将地址转化成对应的行列时需要用到多路复杂器。
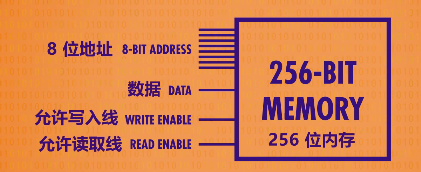
将256位内存抽象成一个整体,如下图,其中:
输入一个8位的地址,4位代表列,4位代表行
允许写入线和允许读取线
一条数据线,用于读/写数据
256位的内存也没法做成什么事,所以还要扩大规模。将之并排放置,像寄存器一样,一行8个,这样每个存一位,一行8个就可以存一个8位的数字,也就是可以存一个字节。为了存一个8位的数字,同时给这8个256位内存一样的地址,每个地址存一位,这就意味着总共可以存储256个字节。
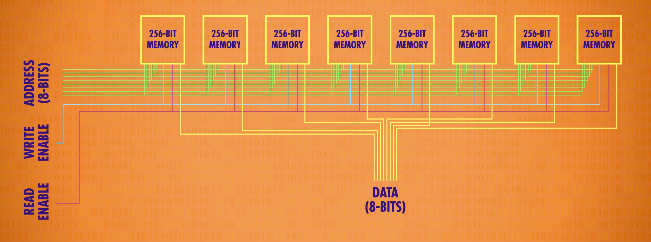
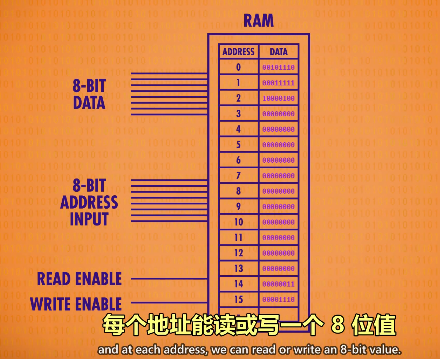
抽象一下,将之看成一个整体的可寻址内存,有256个地址,每个地址能读或写一个8位值
这样不断的把内存打包到更大的规模,就可以扩展到上兆字节(MB)和千兆字节(GB)的现代计算机,随着内存地址的增多,内存地址也必须增长,8位最多可以代表256个内存地址,更多字节的存储就需要32位的地址。
内存的一个重要的特性是:可以随时访问任何位置,因此称之为“随机存取存储器”(Random Access Memory或RAM)
看一下下图的内存,上面焊了8个内存模块

打开一个,然后放大,会看到32个内存方块
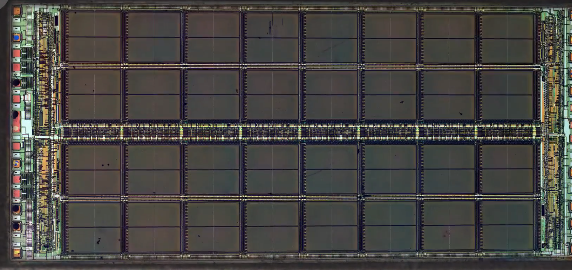
放大其中一个方块,看到有4个小块

再放大,就可以看到存储“位”的矩阵,这个矩阵是128位 * 64位,总共8192位,一层层叠加,8192 * 4 * 32 * 8 = 800万位,也就是1兆字节(1 MB)。

矩阵层层嵌套,来存储大量的信息。就像计算机中的很多事情,底层都很简单,让人难以理解的是,一层层精妙的抽象。


