参考博客:
https://blog.csdn.net/qq_40772692/article/details/79343914
一、二叉树的常用性质
<1>.在二叉树的第i层上最多有2 i-1 个节点 。(i>=1)
<2>.二叉树中如果深度为k(有k层),那么最多有2k-1个节点。(k>=1)
<3>.若二叉树按照从上到下从左到右依次编号,则若某节点编号为k,则其左右子树根节点编号分别为2k和2k+1;
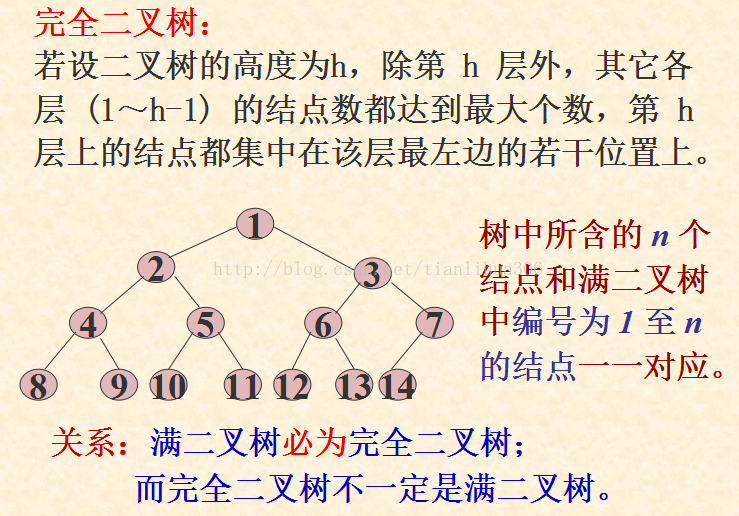
<4>.二叉树分类:满二叉树,完全二叉树
<5>.在完全二叉树中,具有n个节点的完全二叉树的深度为[log2n]+1,其中[log2n]+1是向下取整。满二叉树的深度为k=log2(n+1);
满二叉树:高度为h,由2^h-1个节点构成的二叉树称为满二叉树。
<6>二叉树的度:二叉树中的某个节点的直接后继节点数量(不超过2);

二、二叉树的三种遍历方式
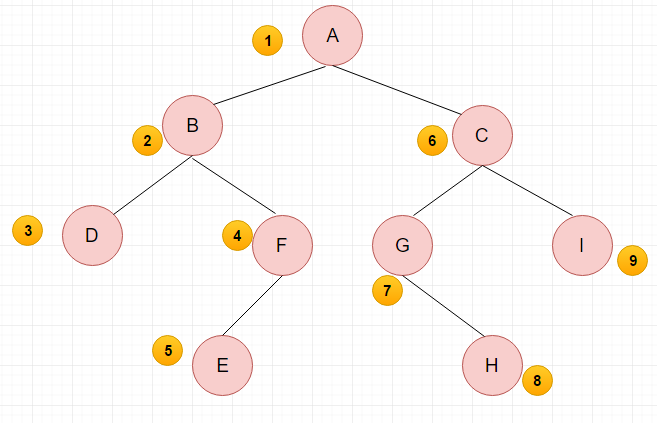
(1)先序遍历:根节点 -> 左子树 ->右子树
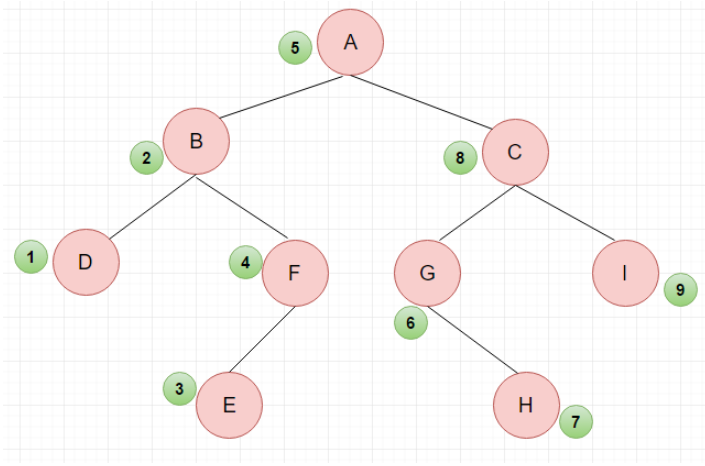
(2)中序遍历:左子树 -> 根节点 -> 右子树
(3)后序遍历:左子树 -> 右子树 -> 根节点

获得遍历顺序的方法原则就是:采用递归的方式遍历
下面是参考的网上的一个二叉树实现以及三种遍历方式的代码,如下:
//实现普通的二叉树,以及三种遍历方式 #include<iostream> using namespace std; typedef char ElemType; //二叉树的结构 typedef struct BiTNode{ ElemType data; struct BiTNode * lchild, *rchild; }BiTNode , *BiTree; //使用递归的前序方式建立二叉树 void CreateBiTree(BiTree *T) { ElemType ch; cin >> ch; if (ch == '#') *T = NULL; //保证是叶节点 else { *T = (BiTree)malloc(sizeof(BiTNode)); (*T)->data = ch; //生成节点 CreateBiTree(&((*T)->lchild)); //构造左子树 CreateBiTree(&((*T)->rchild)); //构造右子树 } } //将遍历得到的节点输出 void operation_1(ElemType ch) { cout << ch << " "; } //将遍历得到的节点输出,同时输出层数 void operation_2(ElemType ch, int level) { cout << ch << "在第" << level << "层" << endl; } //递归前序方式遍历 void PreOrderTraverse(BiTree T, int level) { if (T == NULL) return; operation_2(T->data, level); //输出信息,其实也是先访问根节点 PreOrderTraverse(T->lchild, level + 1); //再递归访问左子树 PreOrderTraverse(T->rchild, level + 1); //右子树 } //递归中序方式遍历 void InOrderTraverse(BiTree T, int level) { if (T == NULL) return; InOrderTraverse(T->lchild, level + 1); //左子树 operation_2(T->data, level); //根节点,其实输出也是“根节点” InOrderTraverse(T->rchild, level + 1); //右子树 } //递归后序方式遍历 void PostOrderTraverse(BiTree T, int level) { if (T == NULL) return; PostOrderTraverse(T->lchild, level + 1); //左子树 PostOrderTraverse(T->rchild, level + 1); //右子树 operation_2(T->data, level); //根节点 } int main(int argc, char *argv[]) { int level = 1; BiTree T = NULL; cout << "请以前序遍历的方式输入扩展二叉树:"; //类似输入AB#D##C## CreateBiTree(&T); //建立二叉树 cout << "递归前序遍历输出为:" << endl; PreOrderTraverse(T, level); cout << endl; cout << "递归中序遍历方式输出为:" << endl; InOrderTraverse(T, level); cout << endl; cout << "递归后序遍历输出为:" << endl; PostOrderTraverse(T, level); cout << endl; system("pause"); return 0; }