从香农的信息熵谈其起,再聊聊逻辑回归和softmax;





softmax loss的梯度求导具体如下(全连接形式):
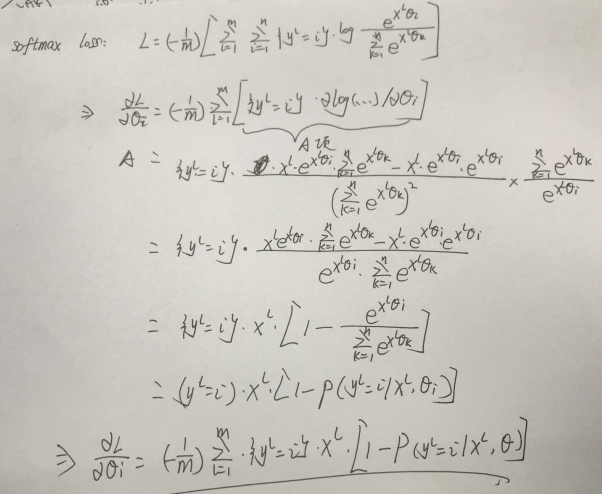
更一般的形式:

前向/反向实现代码如下的两个例子:
例一:
class SoftmaxLayer: def __init__(self, name='Softmax'): pass def forward(self, in_data): shift_scores = in_data - np.max(in_data, axis=1).reshape(-1, 1) #在每行中10个数都减去该行中最大的数字 self.top_val = np.exp(shift_scores) / np.sum(np.exp(shift_scores), axis=1).reshape(-1, 1) return self.top_val def backward(self, residual): N = residual.shape[0] dscores = self.top_val.copy() dscores[range(N), list(residual)] -= 1 #loss对softmax层的求导 dscores /= N return dscores
例二:
""" Structured softmax and SVM loss function. Inputs have dimension D, there are C classes, and we operate on minibatches of N examples. Inputs: - W: A numpy array of shape (D, C) containing weights. - X: A numpy array of shape (N, D) containing a minibatch of data. - y: A numpy array of shape (N,) containing training labels; y[i] = c means that X[i] has label c, where 0 <= c < C. Returns a tuple of: - loss as single float - gradient with respect to weights W; an array of same shape as W """ def softmax_loss_vectorized(W, X, y): loss = 0.0 dW = np.zeros_like(W) num_train = X.shape[0] score = X.dot(W) shift_score = score - np.max(score, axis=1, keepdims=True) # 对数据做了一个平移 shift_score_exp = np.exp(shift_score) shift_score_exp_sum = np.sum(shift_score_exp, axis=1, keepdims=True) score_norm = shift_score_exp / shift_score_exp_sum loss = np.sum(-np.log(score_norm[range(score_norm.shape[0]), y])) / num_train # dW d_score = score_norm d_score[range(d_score.shape[0]), y] -= 1 dW = X.T.dot(score_norm) / num_train return loss, dW
另外补充:
(1)交叉熵在pytorch中的应用,nn.CrossEntropyLoss():

(2)softmax函数求导如下:
