k-均值聚类

K-均值聚类

　　k-均值（k-means Clustering）算法是著名的划分聚类算法。由于他的简洁和效率使得它成为所有聚类算法中最为广泛使用的。

　　给定一个数据点集合和需要的聚类数目K（K是有用户指定的），K-均值算法根据某个距离函数反复的把数据分入K个聚类中。

　　  聚类属于无监督学习，以往的回归、朴素贝叶斯、SVM等都是有类别标签y的，也就是说样例中已经给出了样例的分类。而聚类的样本中却没有给定y，只有特征x，比如假设宇宙中的星星可以表示成三维空间中的点集(x,y,z)。聚类的目的是找到每个样本x潜在的类别y，并将同类别y的样本x放在一起。比如上面的星星，聚类后结果是一个个星团，星团里面的点相互距离比较近，星团间的星星距离就比较远了。

K-均值算法

  k均值算法的计算过程非常直观：

      1、从D中随机取k个元素，作为k个簇的各自的中心。

      2、分别计算剩下的元素到k个簇中心的相异度，将这些元素分别划归到相异度最低的簇。

      3、根据聚类结果，重新计算k个簇各自的中心，计算方法是取簇中所有元素各自维度的算术平均数。

      4、将D中全部元素按照新的中心重新聚类。

      5、重复第4步，直到聚类结果不再变化。

      6、将结果输出。

    在算法的开始，先从随机选取k个数据点作为初始的种子（seed）聚类中心，然后计算每个数据的点与各个种子聚类中心之间的距离，把每个数据点分配给距离它最近的聚类中心。聚类中心以及分配给它的数据点就代表一个聚类，一旦全部的数据点都被分配完，每个聚类的聚类中心以及分配烦人中心会根据给聚类中现有的数据点重新计算。计算的过程将被不断重复知道满足某个终止条件。

       终止（收敛）条件可以是一下任何一个：

（1）    没有（或最小数目）数据点被重新分配到不同的聚类。

（2）    没有（或最小数目）聚类中心没有发生变化。

（3）    误差平方和（SSE）局部最小

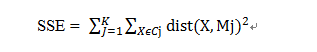
其中k表示需要的聚类数目，Cj表示第j个聚类，Mj是聚类的聚类中心（中所有数据点的均值向量），dist（X,Mj）表示数据点和聚类中心的距离。

在那些均值能被定义和计算的数据集上的均能使用K-均值算法。在欧式空间中聚类的均值可以用下式计算：

 

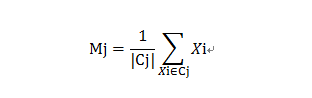
其中|Cj|表示Cj中的数据点的个数。数据点和聚类均值（中心）之间的距离可以被计算如下：