理论部分:
代码部分:
import random
import matplotlib.pyplot as plt
import numpy as np
position = 0
walk = [position]
steps = 1000
for i in range(steps):
step = 1 if random.randint(0, 1) else -1
position += step
walk.append(position)
#plt.plot(walk[:1000])
nsteps = 1000
draws = np.random.randint(0, 2, size=nsteps)
steps = np.where(draws > 0, 1, -1)
walk = steps.cumsum() # 一维向量就可以这样来
#plt.plot(walk[:1000])
print( "min:" + str(walk.min()) )
print( "max:" + str(walk.max()) )
# 需要多久才能距离初始0点至少10步远(任一方向均可)
print((np.abs(walk) >= 10).argmax())
nwalks = 5000
nsteps = 1000
#模拟多个随机漫步过程(比如5000个)
draws = np.random.randint(-1, 1, size=(nwalks, nsteps)) # 0 or 1
print(draws)
steps = np.where(draws >= 0, 1, -1)
print(steps)
walks = steps.cumsum(1)
print(walks)
print("max: " + str(walks.max()) )
print("min: " + str(walks.min()))
# 用any方法来对此进行检查 因为不是5000个过程都到达了30的距离
hits30 = (np.abs(walks) >= 30).any(1)
print("sum: " + str(hits30.sum()) ) # Number that hit 30 or -30
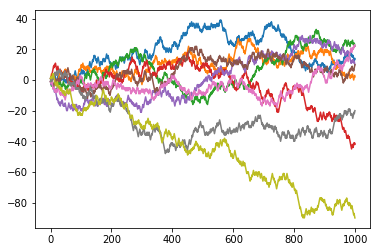
plt.plot(walks[0])
plt.plot(walks[1])
plt.plot(walks[2])
plt.plot(walks[3])
plt.plot(walks[4])
plt.plot(walks[5])
plt.plot(walks[6])
plt.plot(walks[7])
plt.plot(walks[8])
https://www.jianshu.com/p/numpy_test