[模板] [洛谷] 线性筛素数 P3383 P1865

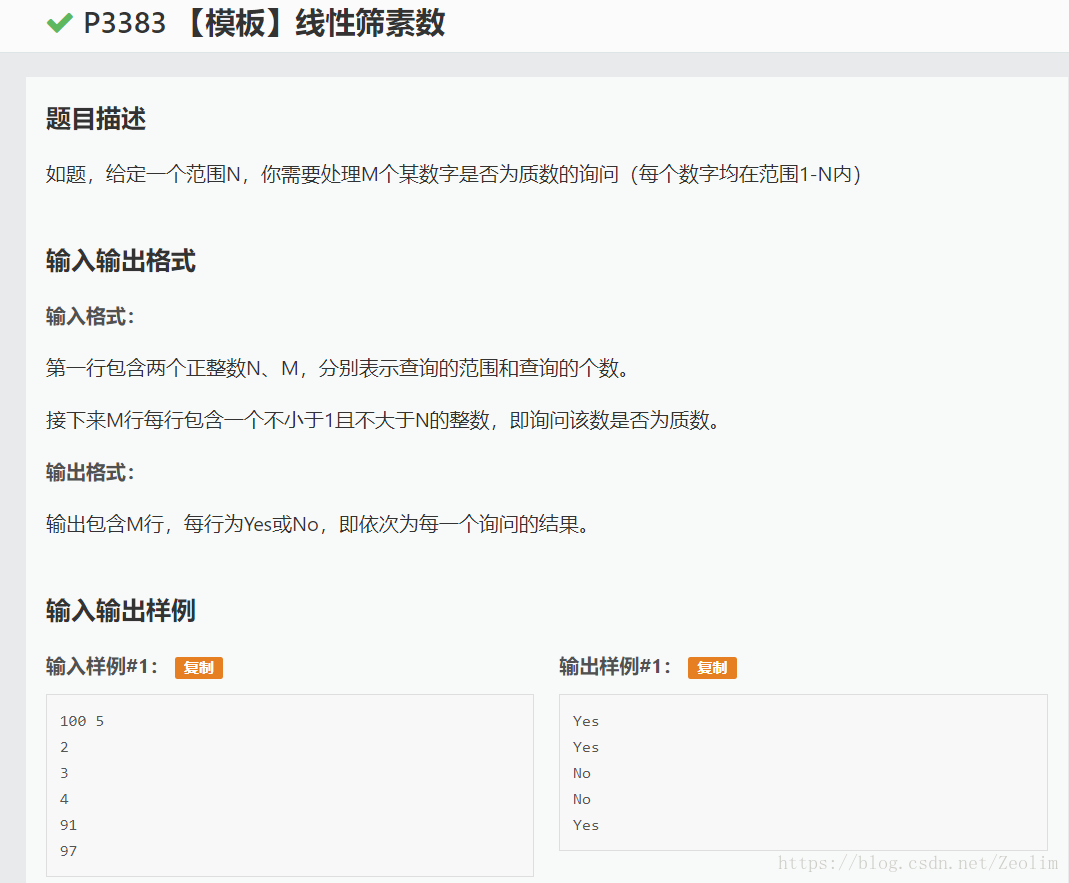
P3383 线性筛素数

 重复筛

bool check[maxn];
ll n, m;
void initprime()
{
    check[1] = check[0] = true;

    for(int i = 2; i <= n; i ++)
    {
        if(!check[i])
        {
            for(int j = 2 * i; j <= n; j += i)
            {
                check[j] = true;
            } 
        }
    }
}

 欧拉筛

#include <iostream>
using namespace std;

const int MAXN = 1e7 + 10;

int check[MAXN] = {0};

int prime[MAXN] = {0};

int pos = 0;

int flag;


void initprime(int len)
{
	for(int i = 2; i < len; i++)
	{
		if(!check[i])
			prime[pos++] = i;
			
		for(int j = 0; j < len && i * prime[j] < len; j++)
		{
			check[i * prime[j] ] = 1;
			
			if(i % prime[j] == 0)
				break;
		}
	}
}

bool bserch(int x)
{
	int fst = 0, lst = pos - 1, mid;
	
	while(fst <= lst)
	{
		mid = (fst + lst) / 2;
		
		if(prime[mid] > x)
			lst = mid - 1;
		else if(prime[mid] < x)
			fst = mid + 1;
		else
			return true;
	}
	
	return false;
} 

int main()
{
	int len, t;
	
	cin>>len>>t;
	
	initprime(len + 1);
	
	while(t--)
	{
		int tmp;
		
		cin>>tmp;
		
		if(bserch(tmp))
		{
			cout<<"Yes"<<endl;
		}
		
        else
		{
			cout<<"No"<<endl;
		}
	}
	
		
	return 0;
}

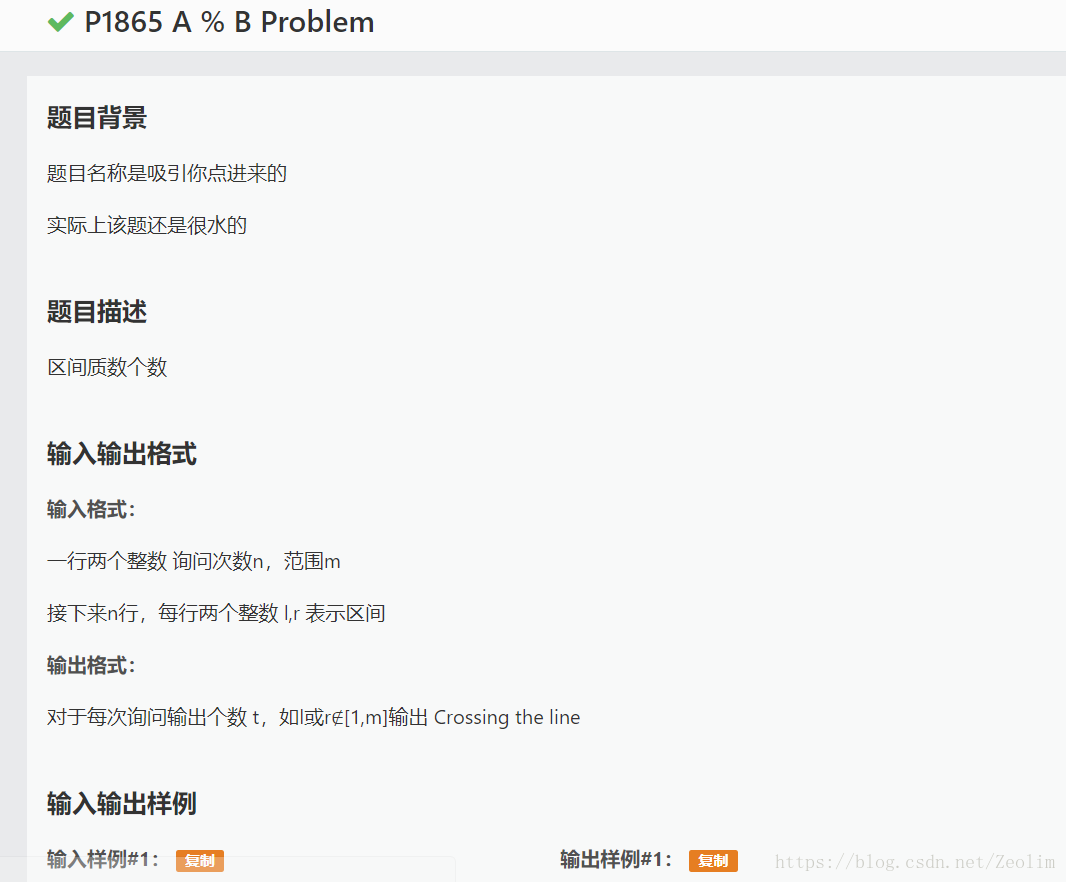
P1865 

线筛+二分寻下届

效率非常高

#include <iostream>
using namespace std;

const int MAXN = 1e7 + 10;

int check[MAXN] = {0};

int prime[MAXN] = {0};

int pos = 0;

int flag;


void initprime(int len)
{
	for(int i = 2; i < len; i++)
	{
		if(!check[i])
			prime[pos++] = i;
			
		for(int j = 0; j < len && i * prime[j] < len; j++)
		{
			check[i * prime[j] ] = 1;
			
			if(i % prime[j] == 0)
				break;
		}
	}
}

int bserch(int x)
{
	int fst = 0, lst = pos - 1, mid;
	
	while(fst < lst)
	{
		mid = (fst + lst) / 2;
		
		if(prime[mid] >= x)
			lst = mid;
		
        else
			fst = mid + 1;
	}

	return fst;
} 

int main()
{
	int len, t;
	
	cin>>t>>len;
	
	initprime(len + 10);
	
	while(t--)
	{
		int a, b;
		
		cin>>a>>b;
		
		if(a < 1 || b > len)
        {
            cout<<"Crossing the line"<<endl;
        }

        else
        {
            int ans = 0;

            int p, q;

            p = bserch(a);

            q = bserch(b);

            ans = q - p;

            if(prime[q] <= b)
                ans++;

            cout<<ans<<endl;
        }
	}
	
		
	return 0;
}