题目
-
给定正整数 $n$,求如下式子的值:
$$sum_{i=1}^n lfloor frac{n}{i} floor$$
- 答案对一个数取模,$n le 10^{15}$,时间限制 2s。
思考
如果我们暴力求解,复杂度是 $O(n)$ 的,那程序几天也跑不完。
思考一下,其实我们的瓶颈,就是出于 $i$ 太多了。
那枚举什么量,才能让枚举的数量变少?
请看下面这张图,这是一个反比例函数图象的其中一支(图片绘于 desmos):
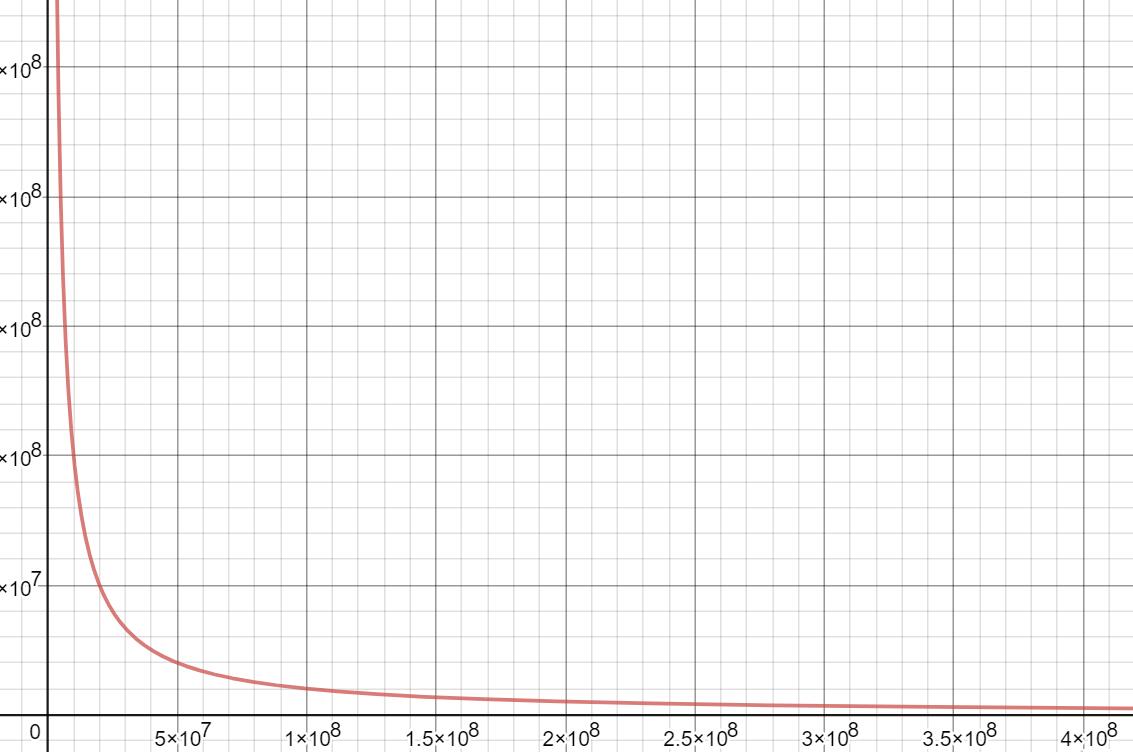
我们把 $f(x)=frac{10^{15}}{x}$,$y=lfloor f(x) floor$ 的图象画了出来。
明显地看到,在 $x$ 比较大的时候,$frac{10^{15}}{x}$ 十分靠近 $x$ 轴。
这么说明,随着 $x$ 越来越大,相同的 $y$ 的值也会越来越多。
像 $n=10^{15}$ 的时候,$frac{10^{15}}{5 imes 10^{14}+1}$ 到 $frac{10^{15}}{10^{15}}$ 下取整的值都是 1。
按照刚刚的枚举方法,相当于你有约一半的枚举量都浪费于答案为 1 的情况了。
那……我们枚举答案?
好办法!
整除分块
一个数字,最多有多少个因数?
最理想的状态下,这个数满足:$forall i in [1,sqrt{n}], i mid n$。
为什么这个数是最理想的,因为如果 $i$ 大于 $sqrt{n}$,且 $i mid n$,则 $frac{n}{i}$ 肯定在 $[1, sqrt{n}]$ 范围内,必出现过。
所以这个数就是因数尽可能多的数。
同时有一个结论,若 $i mid n$,则 $frac{n}{i} mid n$。
所以,$n$ 的因数个数最多不超过 $2 imes sqrt{n}$,取整后的不同答案也不会超过 $2 imes sqrt{n}$。
因此,不同答案的个数不超过 $2 imes sqrt{n}$。
而观察数据范围,$2 imes sqrt{n}$ 在可以接受的范围内。
如果能够设计出一种刚好能枚举所有因数的算法,这道题就可以被解决。
现在来推导一下:
- 不论 $n$ 取多大,$n$ 一定为它自己的因数,以下以 $n=10$ 为例。
- 因此,当 $iin [1,1]$ 时,$frac{10}{i}$ 答案为 $10$。
- 接下来让枚举区间左端点设为原右端点 + 1,即 $[2,1]$。
- 容易得到,这时区间内每个数的答案均为 $lfloorfrac{10}{2} floor=5$,即为 $a$。
- 可以得出右端点 $r=lfloorfrac{10}{5} floor=2$。
- 此时答案区间为 $[2,2]$,累计为 $a imes (r-l+1)=5$。
- 当区间 $[3,3]$ 计算完毕时,左端点变为 $2+1=3$。
- 此时区间内每个数答案均为 $lfloorfrac{10}{3} floor=3$。
- 可以得出右端点 $r=lfloorfrac{10}{3} floor=3$。
- 此时答案区间为 $[3,3]$,累计为 $3 imes (3-3+1)=3$。
- 当区间 $[3,3]$ 计算完毕时,左端点变为 $3+1=4$。
- 此时区间内每个数答案均为 $lfloorfrac{10}{4} floor=2$。
- 可以得出右端点 $r=lfloorfrac{10}{2} floor=5$。
- 此时答案区间为 $[4,5]$,累计为 $2 imes (5-4+1)=4$。
- 最后,左端点变为 $5+1=6$。
- 此时区间内每个数答案均为 $lfloorfrac{10}{6} floor=1$。
- 可以得出右端点 $r=lfloorfrac{10}{1} floor=10$。
- 此时答案区间为 $[6,10]$,累计为 $1 imes (10-6+1)=5$。
- 发现右端点已经到 $n$ 了,停止算法。
- 答案为 $10+5+3+4+5=27$,与 $10+5+3+2+2+1+1+1+1+1=27$ 一致。
很明显,这个算法将 $frac{n}{i}$ 相同的情况整合到一块共同处理,效率提高不少。