基础算法戳这里
扩展一:二阶前缀和
给定一个 $n imes m$ 的矩阵,有 $T$ 次询问,每次会给出四个数 $a,b,c,d$,求以点 $(a,b)$ 为左上角,点 $(c,d)$ 为右下角的矩形所有元素和。
$1 le n,m le 3000$,$1 le T le 10^6$。
我们先把问题变简单:如何用二维前缀和求出整个矩阵的和?
观察一维递推式:$S_i=S_{i-1}+a_i$。
那么二维递推式大概长这样 $S_{i,j}=F+a_{i,j}$,$F$ 为由前面递推出的数字。
先假设 $F=S_{i-1,j}+S_{i,j-1}$,但是很容易推翻这个假设,因为从 $(1,1)$ 到 $(i-1,j-1)$ 之间矩阵的所有数被算了两次。
所以按照容斥原理,累加值应该减去一份 $S_{i-1,j-1}$。
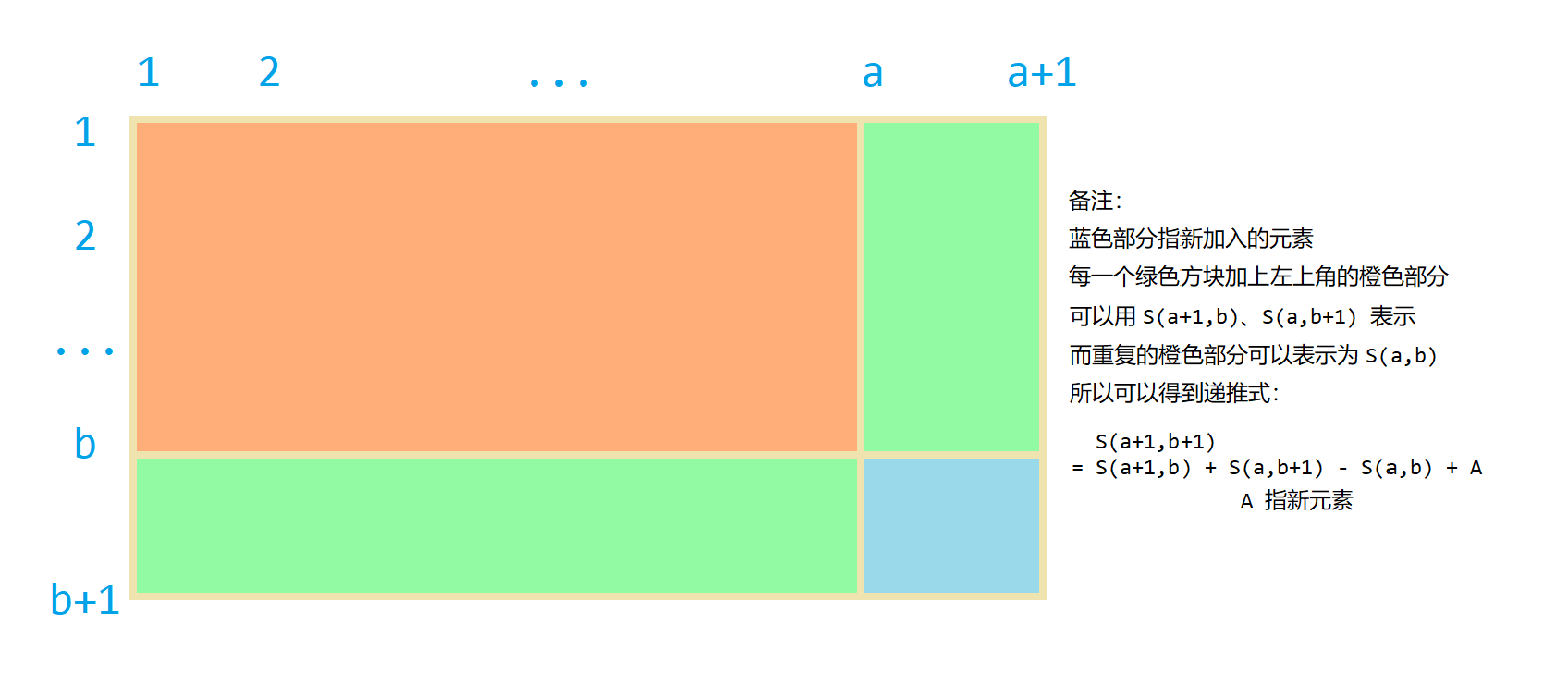
所以 $S_{i,j}=S_{i-1,j}+S_{i,j-1}-S_{i-1,j-1}+a_{i,j}$,而整个矩阵的和就是 $S_{n,m}$。
看不懂过程的可以看看下面的图片帮助理解:
然后是第二个问题:怎么 $O(1)$ 查询任意一个子矩阵的元素和?
首先,$(1,1)$ 到 $(c,d)$ 的元素和为 $S_{c,d}$。
和之前一样,我们需要减去多余的部分,也就是 $S_{a-1,d}$ 和 $S_{c,b-1}$。
而且要把减多的还回来,加上 $S_{a-1,b-1}$。
也就是:$ exttt{Answer}=S_{c,d}-S_{c,b-1}-S_{a-1,d}+S_{a-1,b-1}$。
图片解释:
