CF

$ ext{A. Prefixes}$

题意：

　　给定一个序列，只包含 $a$ 或者 $b$，现在要修改这个序列，使得这个序列的长度为偶数的前缀子串中，$a$ 的个数和 $b$ 的个数一样多。

　　序列长度不超过 $2*10^5.$

解析：

　　这道题，表面上很困难，实际只需要这么想：

　　我们只需要每两个字符检查一次，如果这两个字符相同那么就将其中一个改成另一种字符即可。

　　复杂度 $O(n).$

$ ext{B. Shotting}$

题意：

　　你有一个长度为 $n$ 的序列 $A$，即 $A_1,A_2,...,A_n.$

　　现在，请重新给序列 $A$ 排序，使得 $large{sum}{^n_{i=1}(i-1)*A_i+1}$ 最小。

　　$1 le n,A_i le 10^3.$

解析：

　　我们发现序列中每一个数的权重是不同的，越前面的数权重越小。

　　所以，我们想要让答案最小，那么一定要让大的数排在前面，小的数排在后面。

　　这样，就可以得到正确答案了。

$ ext{C. White Sheet}$

题意：

　　给定一张白纸和两张黑纸（均为矩形）的左下角、右上角的坐标，如果两张黑纸完全覆盖白纸，输出 $NO$，否则输出 $YES.$

　　$0 le ext{每个点的坐标} le 10^6.$

解析：

　　首先我们可以想到，如果这张白纸可以被其中一张黑纸完全覆盖，那么肯定输出 $NO.$

　　否则，若这两张黑纸无交集，肯定输出 $YES.$

　　做完了？不可能！

　　看这个图：

　　

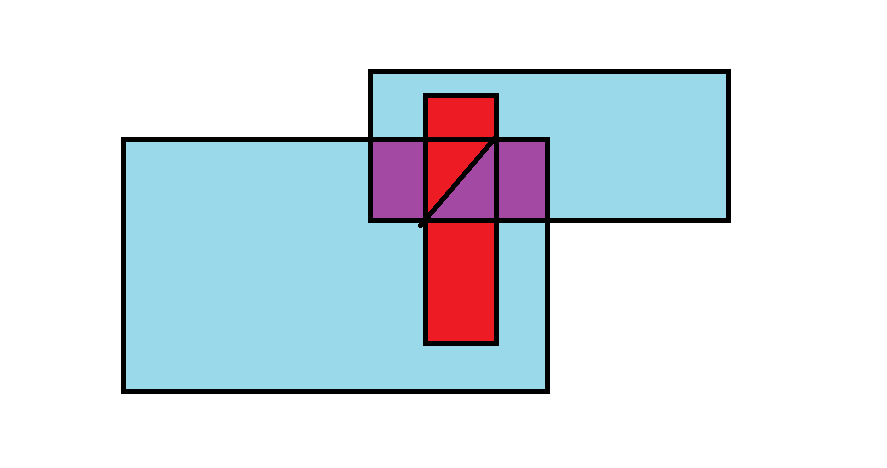
　　其中，红色是白纸，青色是黑纸，紫色是黑纸的交集。

　　我们发现，白纸置于如下绿色+紫色区域时，黑纸可以完全覆盖白纸，如下图：

　　

　　因此，我们只要分别判断白纸位于绿色区域就行了。

　　判断方式，看白纸是否位于“横着”或“竖着”的任意一个绿色矩形。

$ ext{D. Swords}$

题意：

　　有 $n$ 堆剑，每一堆有 $m$ 个剑。

　　现在，有 $k$ 个人偷窃了这些剑，每一个人偷了相同数量的剑。

　　给出每一堆剩余剑的数量 $A_1,A_2,...,A_n$，求出 $k$ 的最小值且求此时的 $m.$

　　$0 le A_i le 10^9$，$1 le n le 2*10^5.$

解析：
　　这道题不保证答案具有单调性，所以不能用二分答案；

　　然后，就试着用快速做法来解决。

　　我们可以求得 $m=gcd{m-A_i}.$

　　那么，如何快速求出 $m$ 呢？

　　差分！

　　用差分，就可以抵消掉 $m$，得到两个数的差。

　　而且，如果 $x|A_i$，$x|A_j$，那么 $x|(A_i-A_j)$

　　所以，这样就可以求出最小的 $m$，并且求出 $k$ 的最小值。