P.S. 彩色字体可以点
$ ext{A. Choose Two Numbers}$
题意:有两个数组,要从两数组各选出一个数,使得它们的和不在任何数组中出现。
这道题的数据范围很小,是签到题,但是这改变不了我交错一发的事实
由于所有数字均不超过 $200$,可以开一个桶来记录是否出现。
之后枚举即可。
$ ext{B. Make Product Equal One}$
题意:有一个长度为 $N$ 的序列,将一个数字加一或减一需要花费 $1$,求最小花费,使得整个序列的积变成 $1.$
$1 le N le 10^5$
这道题问题在于:$-1 imes-1=1$,如何处理负负得正的事情?
我们可以使用贪心策略:负数变成 $-1$,正数变成 $1.$
那么,如果这样操作成绩是 $-1$,那么将答案加二,否则直接输出就可以。
但是,我们忽略了 $0$!
不难发现,$0$ 变成 $1$ 和 $-1$ 都要花费 $1.$
因此,只要这个序列有 $0$,直接按照如上策略,不管乘积正负,直接输出答案就可以。
$ ext{C. Almost Equal}$
题意:构造一个 $1$ 到 $2n$ 的一个排列,让这个排列形成一个首尾相接的环,并且环上任意连续 $n$ 个数的和之差不超过 $1.$
$1 le n le 10^5.$
如果没有答案,输出 $-1.$
下面是一些好方法:
- DFS 找规律
因为爆搜搜出的所有合法序列的规律是相同的,所以这是一个很好的东西。
用 DFS 可以去枚举 $N=2,3,4,5,6$ 五种情况,足够找规律了。
- 数学方法
如果 $n$ 为偶数,易知 $sum_{i=1}^{2n}i$ 为 $n$ 的倍数且不为 $2n$ 的倍数。
所以 $sum_{i=1}^{2n}i$ 为 $n$ 必为 $2$ 的倍数。
我们随便将这个环对半砍,那么这两半的值一定相等,否则它们的差为 $2$,不满足条件。
比如这样($N=4$):
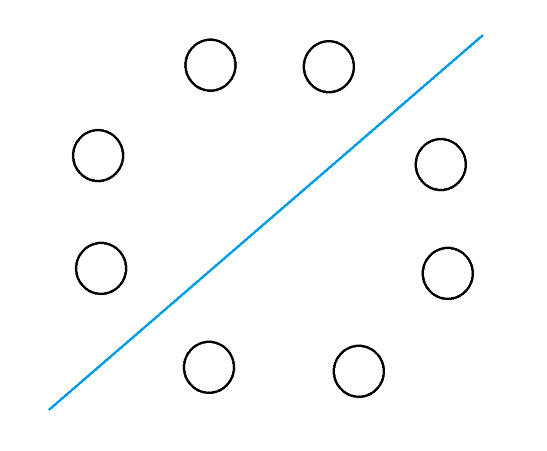
那么这两块的和必定相等。
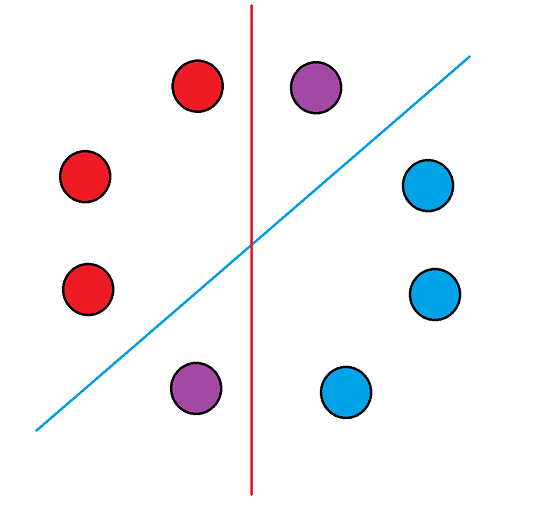
我们换一个角度切:

道理相同。
因为总和相同,所以砍成两半的值也是相同的
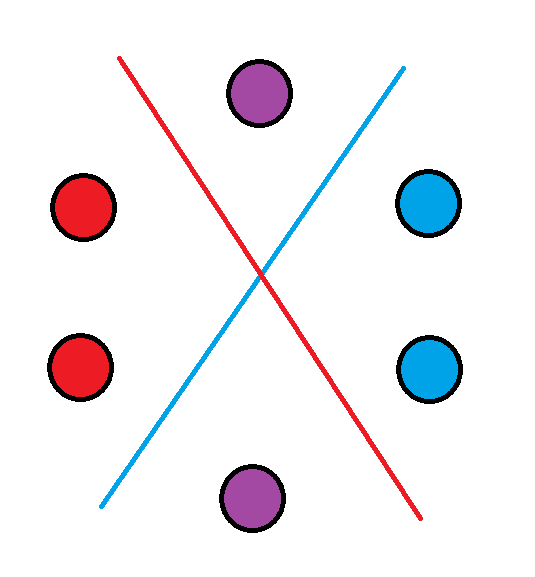
所以:
红点 * 3 + 上面的紫点 = 红点 * 3 + 下面的紫点 = 总和的一半。
所以两个紫点的值相同。
但排列的元素是两两不同的,矛盾。
因此,$n$ 为偶数的时候无解。
然后我们思考 $n$ 为奇数的时候。
当 $n$ 为奇数时,$sum_{i=1}^{2n}i$ 必为奇数
因此,就可以砍出差为 $1$ 的两半了。
当 $n=3$ 的时候,和为 $21$,因此可以砍成两半,分别为 $10$ 和 $11.$
我们先砍两刀:
我们就可以得出,两个紫点的差必为 $1$,否则不成立。
其它也一样。
所以第一个结论是相对的点差为 $1.$
然后我们想如何构造使得两半差为 $1.$,如下图:
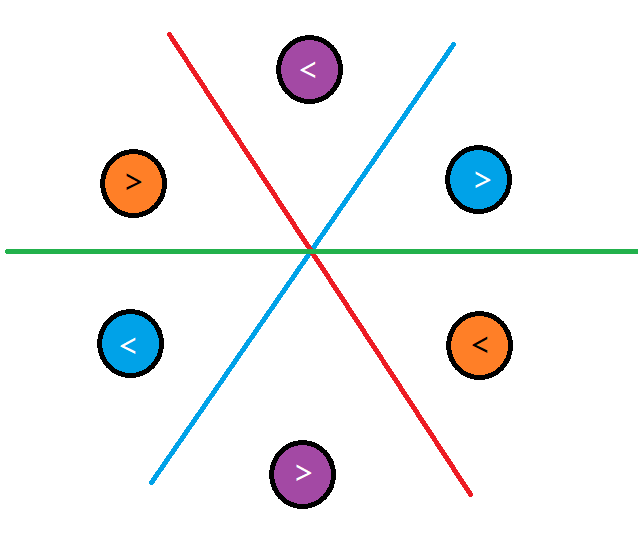
大于号的意义是相同颜色的点相对编号较大的点。
所以策略出来了:
按顺序把每一对点分别赋值为 $(1,2),(3,4),...,(2n-1,2n)$
然后如果我们选定一个点为“大于号”,那么它的两边必须是小于号。
看构造伪代码($n$ 为奇数):
int ans[200010]; for i=1 to n if i % 2 == 1 ans[i] = 2 * i - 1 ans[i + n] = 2 * i else ans[i] = 2 * i; ans[i + n] = 2 * i - 1; }
后面的先咕着