位运算
所有的位运算都是在二进制下实现的。
基本操作:
左移:$x << y$:将 $x$ 在二进制下左移 $y$ 位,相当于 $x*2^y$
右移:$x >> y$:将 $x$ 在二进制下右移 $y$ 位,相当于把这个数二进制下的末 $y$ 位变成 $0$,再乘 $2^{-y}$
按位与:$ ext{a & b}$:将 $a$ 与 $b$ 在二进制下对每一位进行与运算
按位或:$ ext{a | b}$:将 $a$ 与 $b$ 在二进制下对每一位进行或运算
异或:$ ext{a ⊕ b}$: 将 $a$ 与 $b$ 在二进制下对每一位进行异或运算
应用:
以下第 $x$ 位代表从低位到高位的第 $x$ 位,且每一个指令执行的时间复杂度为 $O(1)$
求二进制数 $x$ 第 $k$ 位的值:$ ext{(x >> (k - 1)) & 1}$ 或 $ ext{x & (1 << (k - 1))}$
求二进制数 $x$ 最末尾的 $1$ 所在的位数:$ ext{x & (-x)}$
修改二进制数 $x$ 第 $k$ 位为 1:$ ext{x |= (1 << (k - 1))}$
当然,有一个很优秀的二进制数组:$ ext{bitset}$,它就可以像一个二进制数一样操作
排序
常见的排序
$O(n^2)$:选择排序,冒泡排序,插入排序
$ ext{O(n log n)}$:快速排序,归并排序,堆排序
其它排序:桶排序,计数排序,基数排序,这些排序虽然快,但要保证空间不能爆掉
应用
有一个长度为 $n$ 的序列 $A_1, A_2, ..., A_n$(升序排列)
$n$ 为奇数时,中位数:$A_{(n+1)/2}$
$n$ 为偶数时,中位数:$frac{A_{n/2} + A_{n/2+1}}{2}$
离散化
作用:将无限多的集合映射成有限集合
两种做法:
① $ ext{std::unique}$
② 手动离散化(排序,再开一个数组记去重的序列)
二分
二分是一种逆向思维的算法,即不正向寻找答案,而是以最快的效率在一个单调区间枚举答案。
二分需要:
左端点 $l$,右端点 $r$,终止条件,判断答案正误的函数或条件
不同写法要视题目的情况而定。
例子
有个单调递增的序列 $A_1,A_2,...,A_n$,给出 $k$ 个询问,每次给出一个 $x$,求从左到右第一个大于 $x$ 的数所在的位置,没有输出 $-1$
$1le n,k le 2*10^5$,$0 le x le10^9$
画图:
这是一个长度为 10 的序列:

当 $x=10$ 时:
首先,我们设 $l=1, r=n$
然后,找 $l,r$ 区间最中间的数,我一般写成 $(l+r)>>1$
此时中间数的下标是 $(1+10)/2=5$,我们比较发现 $A_5=9$ 比 $10$ 小
那么,答案就肯定不在前 $5$ 个数里面了。
所以,我们把左端点移到第 $5+1=6$ 个位置(蓝色区间代表待搜索区间):
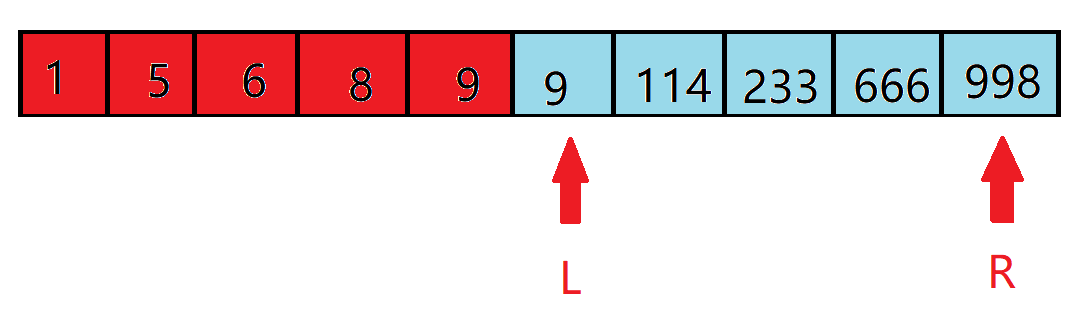
然后这个区间的最中间的下标是 $(6+10)/2=8$,我们发现 $233>10$,符合条件
那么比 $233$ 还大的数也肯定不是答案了。
剩下的区间如下:
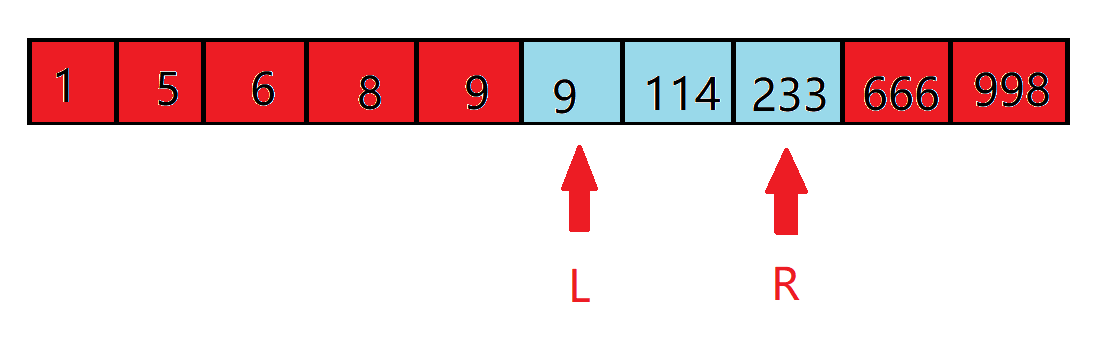
接下来按照这个思路走就行了。
此时中间数的下标为 $(6+8)/2=7$,由于 $A_7=114>10$,于是将答案范围继续缩小:
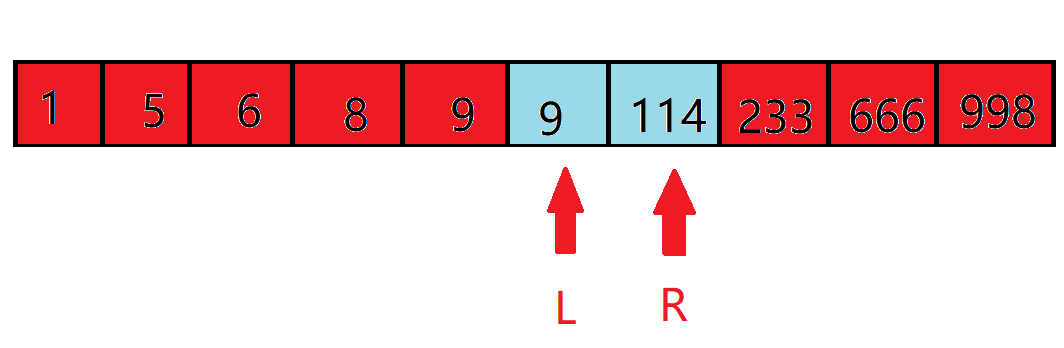
接下来的中间数下标是 $lfloor (6+7)/2 floor = 6$
由于 $A_6<10$,不符合条件,于是将左端点向右调整:
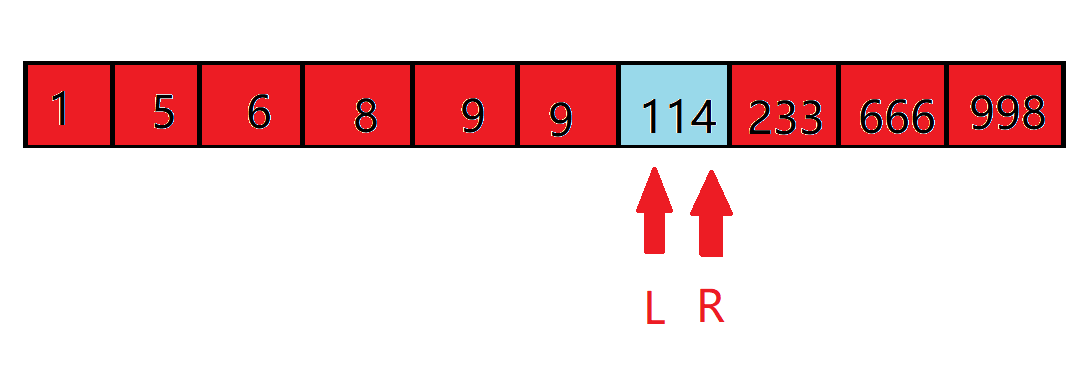
此时我们发现,答案区间只有一个数了,所以这个数就是答案。
差分 & 前缀和
贪心
检查贪心是否成立:出极端数据 $ ext{hack}$ 自己
例子1
有七种硬币,面值分别为 $ ext{1, 3, 9, 27, 81, 243, 729}$ 且每一种硬币均有无限个
现在给出一个 $N$,求最少能用多少硬币使得面值刚好为 $N(1 le N le 10^3)$.
贪心策略:从大的开始取。
比如 $N=1000$,我们就可以取一个 $729$,一个 $243$,一个 $27$,一个 $1$,这是最优答案。
这个例子能用贪心主要原因是三个面值一样小的相当于一个面值大的,所以可以做合并操作。
例子2
有四种硬币,面值分别为 $ ext{1, 5, 10, 11}$ 且每一种硬币均有无限个
现在给出一个 $N$,求最少能用多少硬币使得面值刚好为 $N(1 le N le 10^3)$.
如果我们还是按照那种贪心策略取的话,那么就有可能出问题:
$N=15$ 时,贪心策略是 $11+1+1+1+1=15$,所以贪心的答案为 $5$,但是实际 $10+5=15$,答案是 $2$
所以这个例子需要用 $DP$,方法不在这里阐述。
搜索
- DFS(深度优先搜索)
以递归、回溯的方式完成搜索。
例题:迷宫问题
有一个 $n*m(n,m le 6)$ 的迷宫,中间有若干个障碍,问从 $(1, 1)$ 出发,到达 $(n, m)$ 的总方案数(走过的格子不能再走)。
样例图(黑色方块为障碍,$N=3,M=4$):

我们先随便定一个走迷宫方向的顺序:上,下,左,右,这样做只是方便之后的枚举顺序。
下面,开始 DFS:
$(1, 1)$ 无法向上走,于是向下走 $(2, 1)$
$(2, 1)$ 上面走过,下面不能走,向左走 $(2, 2)$
$(2, 2)$ 向上走 $(1, 2)$
$(1, 2)$ 只能向右走 $(1, 3)$
$(1, 3)$ 无路可走,返回;
$(1, 2)$ 枚举完,返回;
$(2, 2)$ 向下走$(3, 2)$
$(3, 2)$ 只能向右走 $(3, 3)$
$(3, 3)$ 只能向右走 $(3, 4)$;
$(3, 4)$ 为终点,答案加一,返回;
$(3, 3)$ 枚举完,返回;
$(3, 2)$ 枚举完,返回;
$(2, 2)$ 枚举完,返回;
$(2, 1)$ 枚举完,返回;
$(1, 1)$ 向右走 $(1, 2)$
$(1, 2)$ 向下走 $(2, 2)$
$(2, 2)$ 向下走$(3, 2)$
$(3, 2)$ 只能向右走 $(3, 3)$
$(3, 3)$ 只能向右走 $(3, 4)$;
$(3, 4)$ 为终点,答案加一,返回;
$(3, 3)$ 枚举完,返回;
$(3, 2)$ 枚举完,返回;
$(2, 2)$ 枚举完,返回;
$(1, 2)$ 向右走 $(1, 3)$
$(1, 3)$ 无路可走,返回;
$(1, 2)$ 枚举完,返回;
$(1, 1)$ 枚举完,搜索结束。
因此,答案为 $2.$
好用的 STL
-
sort 和 stable_sort
头文件:$ ext{#include <algorithm>}$
这两个都是排序算法,复杂度均为 $ ext{O(n log n)}$,但 $ ext{stable_sort}$ 的复杂度比 $ ext{sort}$ 更加稳定、平均。
用法(以 $sort$ 为例,两个排序写法完全相同):
① $ ext{sort(a, b)}$,代表将一个数组的起始地址 $(a)$ 和结束地址 $(b)$ 之间的元素从小到大排序。
② 如果不想要从小到大,可以自己写一个 $ ext{cmp}$ 函数来控制排序的条件(重载运算符 $<$ 也可以)
- lower_bound 和 upper_bound
头文件:$ ext{#include <algorithm>}$
这两个函数都是在一个单调区间实现查找功能(和二分思想及复杂度相同)
假设有名为 $a$,长度为 $n$ 的数组 $a_1, a_2, ..., a_n.$
$ ext{lower_bound(a + 1, a + n + 1, k) - a}$: $k$ 是一个数,意思是求这个序列中第一个大于等于 $k$ 的数所在位置。
$ ext{upper_bound(a + 1, a + n + 1, k) - a}$: 同上,只是把 “大于等于” 改成 “大于”。
- priority_queue
一个快速求优先级最高的数以及支持插入、删除优先级最高的数的数据结构。
头文件:$ ext{#include <queue>}$
最大:$ ext{priority_queue <Type> A}$
最小:$ ext{priority_queue <Type, vector <Type>, greater <Type> > A}$
$ ext{Type}$ 即类型,其它优先级也可以利用重载运算符定义。
五大操作:
- $A.push(B)$:将 $B$ 插入到优先队列 $A$ 中
- $A.pop()$:将优先队列 $A$ 中优先级最高的元素删去
- $A.top()$:求优先队列 $A$ 中优先级最高的元素
- $A.size()$:求优先队列 $A$ 中元素的个数
- $A.empty()$:判断优先队列 $A$ 是否为空 (空为 $1$,反之为 $0$)
- fill
其实和 $ ext{memset}$ 是差不多的。
头文件:$ ext{#include <algorithm>}$
如果我们有一个数组 $A$,那么将 $A_1$ 到 $A_n$ 的所有元素赋值为 $k$:
$ ext{fill(a + 1, a + n + 1, k)}$ 或 $ ext{fill(&a[1], &a[n], k)}$
- set 和 multiset
头文件:$ ext{#include <set>}$
这是一个方便使用的集合,用红黑树执行。
两者唯一的区别在于 $ ext{set}$ 是不可重集合,但是 $ ext{multiset}$ 可以容纳重复的元素。
- map
头文件:$ ext{#include <map>}$
这是一个可以实现数据映射的东西。
可以直接当作没有下标或下标可以为字符串等类的数组使用。
$ ext{map <Type1, Type2>}$,其中 $ ext{Type1}$ 是下标类型,$ ext{Type2}$ 是映射类型。
- vector
头文件:$ ext{#include <vector>}$
定义:$ ext{vector <Type> A}$,Type 是类型,A 是变量名。
插入 $x$ 和删除末尾元素:$ ext{A.push_back(x), A.pop_back();}$
从小到大排序不定长数组 $v$:$ ext{sort(v.begin(), v.end())};
请注意,插入元素不能直接用数组的方式访问,因为它的下标范围是在随元素个数变化的。
应用:$ ext{vector}$ 代替邻接表
方法:
二维数组存邻接矩阵存不下($N le 10^5$)的时候,所以我们会选择邻接表。
我们也可以用 $ ext{vector}$ 来代替邻接表的作用。
使用方法是,开 $n$ 个 $ ext{vector}$,以 $i$ 为下标的 $ ext{vector}$ 记录所有 $i$ 的出边到达的点的编号。
理由:
给一张图:
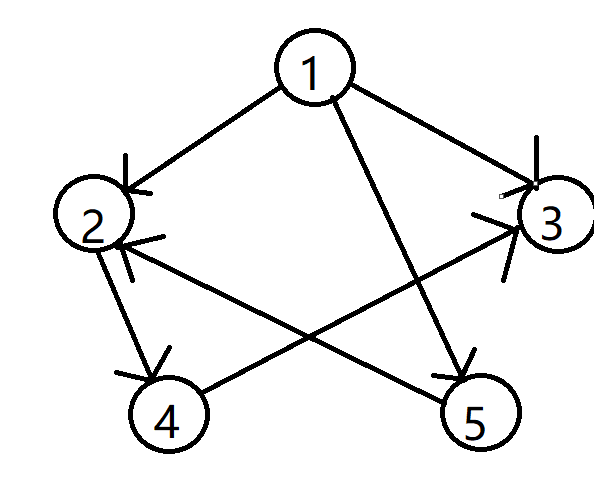
普通数组是这样的:
e[1][1] = 0, e[1][2] = 1, e[1][3] = 1, e[1][4] = 0, e[1][5] = 1; e[2][1] = 0, e[2][2] = 0, e[2][3] = 0, e[2][4] = 1, e[2][5] = 0; e[3][1] = 0, e[3][2] = 0, e[3][3] = 0, e[3][4] = 0, e[3][5] = 0; e[4][1] = 0, e[4][2] = 0, e[4][3] = 1, e[4][4] = 0, e[4][5] = 0; e[5][1] = 0, e[5][2] = 1, e[5][3] = 0, e[5][4] = 0, e[5][5] = 0;
比如从 $1$ 号点开始,我们要从 $1$ 枚举到 $5$,找到所有的从 $1$ 号点出发的边到达的点。
但是用 $ ext{vector}$ 存就不一样了,我们只存从 $1$ 号点出去的点,第二维的记录是一个接一个的,中间没有浪费。
用 $ ext{vector}$ 存是这样的:
(伪代码) vector <int> v[200010]; v[1] 存 {2, 3, 5}; v[2] 存 {4}; v[3] 没有点要存 v[4] 存 {3}; v[5] 存 {2};
$ ext{vector}$ 的元素只存所有出边到达的点的编号,因此 $ ext{vector}$ 存的元素个数就是 $m$ 的大小,和邻接表复杂度相同。
但是如果出题人恶意卡你常数,大部分情况 $ ext{vector}$ 是稍慢于邻接表的。