题解思路
反推排列组合出不重复数字总数m, 然后用N-m
我没感觉这题有关于动态规划 感受不到这题的状态方程
分析过程
来源于leetcode后题解的第一行:
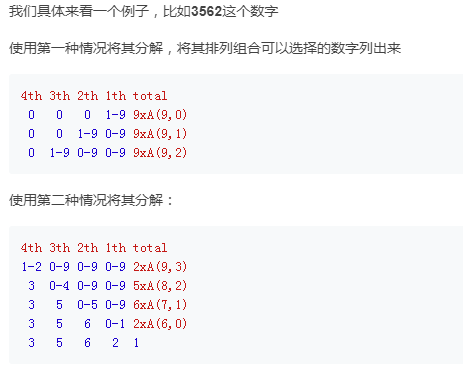
注意的点
- 首先分为首位为0,和首位不为0的情况
- 当首位不为0的时候,对数的每一位上的数限进行划分 比如3562 最高位是 3的时候 就考虑1,2(最高位不为0);百分位 5 的时候就只考虑(0,1,2,4)
- 当确定为上一位的所有情况后,先判断此位前的所有位是否有重复 比如 36340 当考虑百十位的时候 就不用考虑了 因为前面 万 和 百 已经重复
- 最后判断 原数是否是含有重复的数
大多人都用n**2的时间复杂,我是采用集合的方式去过滤重复
给定正整数 N,返回小于等于 N 且具有至少 1 位重复数字的正整数。
如果不存在符合条件的数 那么 至少 是 11
110 111 112 113 都是满足的数字
"""
from functools import reduce
def recursive(m, n):
if n-m < 0:
return 1
return reduce(lambda x, y: x*y, range(m, n+1))
class Solution:
def numDupDigitsAtMostN(self, N: int) -> int:
#当首位数字为零的时3562
length = len(str(N))
total = 0
# 当首位数字为0的时候
for i in range(1, length):
total += 9 * recursive(9-i+2, 9)
# 当首位数字不为0的时候
strs = str(N)
pre = set()
for j in range(length):
currBit = j+1
# 剔除与前面相同的数
# pre = set(map(int, strs[0:j]))
# pre.add(int(strs[j]))
# if strs[j] in num.values():
# print(num.values())
# print(total)
# break
if len(pre) < j:
break
# 当高位数大于1时,说明存在分段 不大于1 那么只能为0
tar = [0, int(strs[j])] if j > 0 else [1,int(strs[j])]
# 当前位数6的 0-5
curr_set = set([i for i in range(tar[0], tar[1])])
if int(strs[j])-1 >= 0:
# 去重
nums = len(curr_set-pre)
# 从0-9是有十个数字呢
total += nums*recursive(11-length,10-currBit)
pre.add(int(strs[j]))
if len(pre)==length:
total += 1
return N - total
if __name__ == '__main__':
res = recursive(8,9)
# print(res)
r = Solution().numDupDigitsAtMostN(3562)
print(r)
