c支持所有数据类型的有符号与无符号运算,尽管c标准没有明确指定某种有符号数的表示,但是几乎所有的机器都使用二进制补码
大多数数字默认是有符号的,当咱们声明一个12345或者0x123,这其实都是有符号的
c在同时包含有符号和无符号的运算,c会把有符号的运算数隐含转换成无符号的运算数(只要含有无符号的数,其他的有符号的数都会被隐含的转换成无符号的数)
一、创建无符号的常量
在常量的后边加上后缀字符“U”或者“u”,比如 12345U 或者 0x123u(大小写都行)
二、转换
c允许有符号与无符号之间的转换,原则是基本的位表示保持不变;
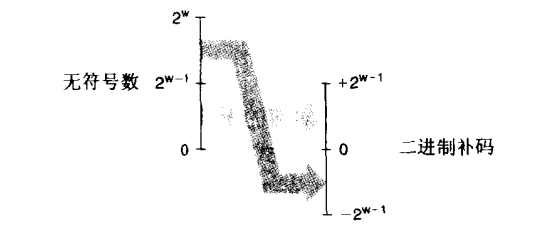
1.无符号转换成有符号,效果就是应用了函数U2Tw,其中w表示数据类型的位数
U2Tw = -xw-12W + X;
 ,从这里可以看出,当 0 <= x < 2w-1的时候是正数,则转换的过程中保持不变; 当 x >= 2w-1的时候,结果是x - 2w,
,从这里可以看出,当 0 <= x < 2w-1的时候是正数,则转换的过程中保持不变; 当 x >= 2w-1的时候,结果是x - 2w,
下面是示意图:
结论:
1>. 对于小的数(< 2w-1):从无符号到有符号的转换将保留数字的原值;
2>.对于大的数(>= 2w-1):从无符号到有符号的转换,数字将被转换为一个负数值
比如:2147483648U,在输出的时候为什么是-2147483648,
过程:因为2147483648 >= 2(32-1),也就是说,它是大的数(>= 2w-1),按照U2Tw的规则,2147483648 - 232 = -2147483648
2.从有符号转换成无符号,效果就是应用了函数T2Uw,其中w表示数据类型的位数
T2Uw = xw-12W + X;
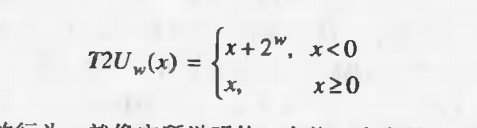 从这里可以看出,当 x >= 0的时候是正数,则转换的过程中保持不变; 当 x < 0的时候是负数,结果是x + 2w
从这里可以看出,当 x >= 0的时候是正数,则转换的过程中保持不变; 当 x < 0的时候是负数,结果是x + 2w
下面是示意图:

结论:
1>.非负数:保持不变
2>.负数:被转变成了大的正数,也就是x + 2w
比如:-1
过程:根据函数规则,负数 -1 + 232 = -4294967297
三、注意事项(下面的观点有误)
1.先看几个练习题:
a. -2147483648 == 2147483648U
b. -2147483648 < -21474836487
c. (unsigned) -2147483648 < -21474836487
d. - 2147483648 < 21474836487
e.(unsigned) -2147483648 < 21474836487
示例:
前面提到过我们创建的数字常量啥的默认都是有符号的,声明无符号的常量在后边加上后缀“U”或者“u”,当两个数进行运算时,只要有无符号数,那么另一个有符号数也会被隐含的转换成无符号数,还有一点,那就是针对超出系统指定位数正数范围的数,在转换的时候,高位是要被舍去的,比如:在8位机器上边,最大的无符号正数也才255,那300,在比较的时候怎么转换呢?
比如 (unsigned) -127 < 300
过程:首先有unsigned声明是无符号的,那么整个运算类型是无符号的,那先来转换一下,-127(有符号转无符号T2Uw)转成无符号的是 -127 + 28 = 129; 那300呢?本身它是个正整数,但是它超出系统8位机最大的unsigned int值(INT_MAX = 255),咱们先把300转成2进制(100101100),从这个二进制可以看出,它是9位,根据系统位数,超出最大范围的数,二进制的最高位要被舍去,保留8位,结果是00101100 = 44,结果可想而知(unsigned) -127(129) < 300(44) 的结果是0
分析练习题:
a. -2147483648 == 2147483648U;2147483648U后缀是“U”,则根据规则 该运算的类型是无符号的,-2147483648根据规则转换成无符号的(-2147483648 + 232 = 2147483648 ),而2147483648由于刚好等于231,而2147483648U它是无符号的,
b. -2147483648 < -21474836487;该运算是有符号类型,同事有符号且是负数的进行比较,这里不难看出来其实-2147483648 > -21474836487,所以结果是0