咕了的构造题单总结

没写完，就被不小心关机了

[ARC103] Robot Arms

link

现在你有 (n) 个点，然后让你构造一个长度为 (m) 的序列，序列中 (d_i) 是每一次移动的距离，输出这个序列，

你对每个点对 ((x_i,y_i)) 每一次从原点出发执行 (m) 次操作,对于每一个指令你可以上下左右任选一个方向走 (d_i) 长度,执行完命令后恰好落到 ((x_i, y_i)),

输出对于每一点对的操作方式((‘U’,‘D’,‘L’,‘R’))

无解输出-1。

• (1le nle 1000, -10^9le x_i le 10 ^9, -10^9 le y_i le 10^9)
• (1le m le 40, 1le d_ile 10^9)
• 均为整数

---

(d_i) 满足 ((x_i, y_i) = (sum_{iin R} d_i - sum_{i in L} d_i,sum_{iin U} d_i - sum_{i in D} d_i))

(x_i + y_i = sum_{iin R | i in U} d_i - sum_{i in L | i in D} d_i)

(x_i + y_i) 与 (sum d_i) 奇偶性相同。

由此可以确定 (sum d_i) 奇偶性。

有解情况必然所有 (x_i+y_i) 奇偶性相同。否则无解。

(log_2 10^9le 30)

能用集合 (d = {1,2,4,8,...,2^k}) 走到任何满足 (|x|+|y| le 2^{k+1}-1) 且 (x+y) 为奇数的点的 ((x, y))，可递推证明

(k = 0, k = 1) 时显然成立，之后递推。

但 (x+y) 可能为偶数，此时增加一个(d_1 = 1) 即可。

输出方案：

如果 (x+y) 为偶数，就先随便乱走一步。((d_1))

转化为 (x+y) 为奇数后，

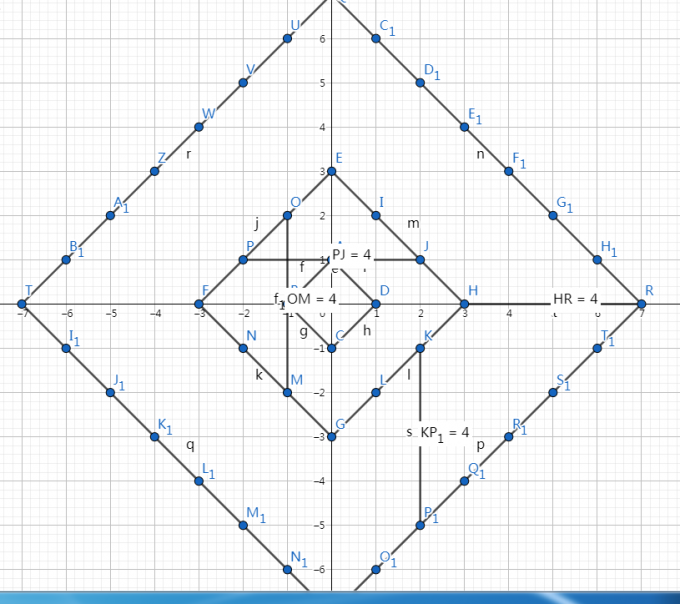
(k = 2) 时，

(P1(2, -5)->K(2, -1)->C(0,-1)->O(0,0))

(N(-2,-1)->K(2, -1)->C(0,-1)->O(0,0))

分别使用了(2^2,2^1,2^0)，每次都对绝对值较大的下手，使得其逼近0。

code

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define make_pair mkp
#define push_back pb
const int N = 1010;
int n, d[35], x[N], y[N], cnt;
void solve(int a, int b){
	for(int i = 1; i <= cnt; i++){
		if(abs(a) > abs(b)){
			int op = a / abs(a);
			if(op == 1) printf("R"), a -= d[i];
			else printf("L"), a += d[i];
		} else {
			int op = b / abs(b);
			if(op == 1) printf("U"), b -= d[i];
			else printf("D"), b += d[i];
		}
	}
	puts("");
	return;
}
int main(){
	scanf("%d", &n);
	int s = 0;
	for(int i = 1; i <= n; i++)
		scanf("%d%d", &x[i], &y[i]), s += ((x[i] + y[i]) % 2 + 2) % 2;
	if(s != 0 && s != n) return puts("-1"), 0;
	if(s == 0) d[++cnt] = 1;
	for(int i = 30; i >= 0; i--)
		d[++cnt] = (1 << i);
	printf("%d
", cnt);
	for(int i = 1; i <= cnt; i++)
		printf("%d ", d[i]);
	puts("");
	for(int i = 1; i <= n; i++)
		solve(x[i], y[i]);
	return 0;
}