回归问题浅析

由于tensorflow2.0版本的更新，很多以前版本上提到的图等概念都不再适用。为了跟上时代的步伐，顺便扎实一下深度学习的基础，从今天开始记录一下学习过程。

要想开始深度学习，首先必不可少的就是数学基础了，虽然tensorflow提供了一系列不需要太深的数学基础就可以使用的现成的函数，但是总吃表面的东西确实没法深入理解，本来是打算开篇做mnist的，为了更深入更全面的了解深度学习，今天就从最简单的回归问题开始。

我们知道，机器学习的目标无非就是从大量数据中学到一些深层次的抽象的概念，即给定一个新情况下的输入x，也能得到一个符合实际情况的输出y。

我们先从最简单的Continuous Prediction（连续值预测）开始，Continuous Prediction的主要目标就是，对于输入数据x，通过给定模型条件 f 和模型参数 θ，能得到相应的f_θ(x)，我们希望f_θ(x)能逼近甚至完全等同于y(其中，y为真实结果，f_θ(x)为预测结果)

现在我们假设给定f :f(x)=w*x+b，为了使(w*x+b-Y)²→0，令损失函数 loss=∑_i(w*x_i+b-y_i)²，令minimize loss，即可得到w'*x+b'→y

那么如何minimize loss呢？我们首先从一个最基本的优化方法“梯度下降”开始。由高等数学导数的特点结合函数图像我们不难得出，导数的方向总是指向函数值变大的方向，我们可以令参数沿着导数相反的方向滑动，从而到达最小loss值。现在假定有这样一个函数

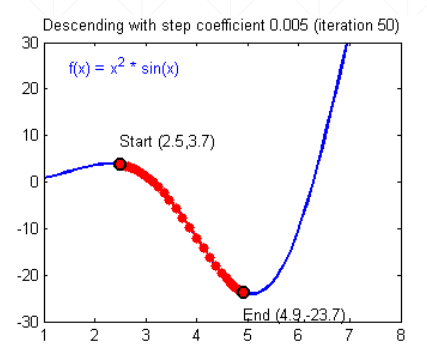
可以看到，要想让参数向loss最优方向滑动，我们给出下面的梯度下降公式

w'=w-lr * dy/dw （其中lr称为衰减因子或衰减学习率，用于控制步长不让它过大，因为滑动步长过大很可能错过最优解区间）

对于f(x)=w*x+b，我们可以通过w'=w-lr * ∂loss/∂w，b'=b-lr * ∂loss/∂b 来调整w和b参数的变化，从而使w'*x+b'→y

下面我们通过使用numpy库来看看线性回归问题的处理效果

首先我们给定100组如下数据，存入Excel，其对应的散点结构如下

    

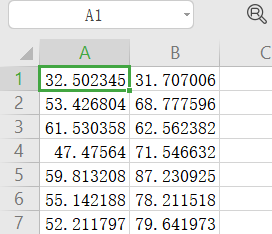
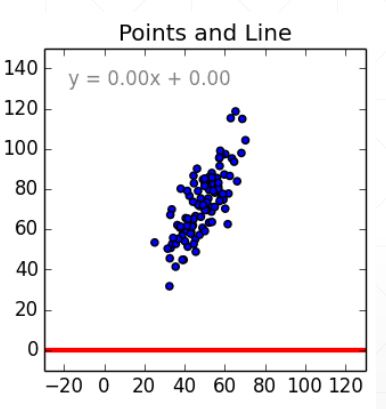
我们通过代码读入数据，梯度下降调整w和b的值，主要代码如下：

# 求损失loss
def compute_error_for_line_given_points(w,b,points):
    totalError=0
    for i in range(len(points)):
        x=points[i,0]
        y=points[i,1]
        totalError+=(w*x+b-y)**2
    return totalError/float(len(points))


# 求下降梯度并更新参数
def step_gradient(w_current,b_current,points,learningRate):
    w_gradient=0
    b_gradient=0
    N=float(len(points))
    for i in range(len(points)):
        x=points[i,0]
        y=points[i,1]
        w_gradient+=(2/N)*((w_current*x+b_current)-y)*x
        b_gradient+=(2/N)*((w_current*x+b_current)-y)

    w_new=w_current-learningRate*w_gradient
    b_new=b_current-learningRate*b_gradient
    return [w_new,b_new]


# 迭代iteration轮后的参数
def gradient_descent_runner(points,starting_w,starting_b,learning_rate,iteration):
    w=starting_w
    b=starting_b
    for i in range(iteration):
        w,b=step_gradient(w,b,np.array(points),learning_rate)
    return [w,b]

经过1000轮迭代后，参数结果如下：

 可以看到，error 从5565下降到112，大概降到初始的1/50，绘制函数图像，和散点大致符合

虽然线性模型在线性回归问题上具有不错的表现，但是它也只能比较好的解决线性可分问题。我们都知道在一定条件下，多层网络模型是由于少层的，但是对于线性模型，多个线性的计算过程完全可以用一个线性计算来表示，比如

对于两层模型输出 y=(xw⁽¹⁾+b⁽¹⁾)w⁽²⁾+b⁽²⁾ ，根据矩阵乘法的结合性，这个公式可以变换如下：y=xw⁽¹⁾w⁽²⁾+b⁽¹⁾w⁽²⁾+b⁽²⁾ ，而w⁽¹⁾w⁽²⁾其实可以被表示为新的参数w'，这样的话，输出关系就可以表示为y=xw'+ b⁽¹⁾)w⁽²⁾+b⁽²⁾，也完全符合线性模型的输入输出线性的相关定义

由此可见，只通过线性变换，任意多层的全连神经网络模型和单层全连神经网络模型的表达能力没有任何区别。但是应用于解决实际问题的模型需要对更复杂的问题具有解决的能力，比如线性不可分或者更高维空间中的分布情况。

下一篇将使用激活函数使模型去线性化，使其不再仅仅是用于解决线性回归问题，并保留线性模型中的参数调整方式，对深度学习中helloworld级别的mnist数据集进行分类