A
题意
要你构造 (n) 个数,每个数的范围是 ([1,4n]),使得其中任意两个数 (a,b) 不满足 (gcd(a,b)=1) 且不满足 (gcd(a,b)=a) 且不满足 (gcd(a,b)=b)
题解
一道一眼构造题。我们发现如果只取偶数的话就不可能出现 ((a,b)=1) 的情况,而又他的范围那么大,所以如果取 (2n+2,2n+4,...,4n) 这 (n) 个数一定不会出现后两种情况。这样就构造完了。
#include <bits/stdc++.h>
using namespace std;
int t;
int n;
int main() {
scanf("%d", &t);
while (t--) {
scanf("%d", &n);
for (int i = 4 * n; i > 4 * n - 2 * n; i -= 2) {
printf("%d ", i);
} printf("
");
}
return 0;
}
B
题意
给你两个数 (a,b) 和一个长度为 (n) 的01字符串。对于一个1的连通块你需要花费 (a) 去炸掉它并且你可以花费 (b) 去把一个0变成1,求你炸掉所有1的最小花费是多少。
题解
从左往右推,把两个1的连通块之间的0的个数记为 (x),如果 (x imes b<a) 的话就把这一段填成1,答案加上 (x imes b),否则则需一段新的1连通块,答案加上 (a)。注意一开始必须有一个1的连通块,即如果存在1的话答案至少为 (a)。
#include <bits/stdc++.h>
using namespace std;
int t;
int a, b;
char s[100010];
int n;
long long ans;
int main() {
scanf("%d", &t);
while (t--) {
ans = 0;
scanf("%d%d", &a, &b);
scanf("%s", s + 1);
n = strlen(s + 1);
bool have = false;
int now = 0;
for (int i = 1; i <= n; i++) {
if (s[i] != s[i - 1]) {
if (s[i] == '1') ans += have ? min(now * b, a) : a, have = true;
now = 1;
} else now++;
}
printf("%lld
", ans);
}
return 0;
}
C
题意
给你两个数列:({a},{b}),要你求出 (min_{Psubseteq {1,2,...,n}}{max{max_{i in P}a_i,sum_{i otin P}b_i}})
题解
此题不需要二分答案,直接排序加枚举即可。我们发现在枚举 (P) 的时候如果对于一个 (i otin P) 且 (a_i le max_{i in P}a_i) 那这个 (i) 也包含进来一定更优。所以我们可以先对 (a) 排序,枚举前 (i) 个人是送外卖的,然后维护一个后缀和就可以了。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll inf = 0x3f3f3f3f3f3f3f3f;
struct node{
int a, b;
friend bool operator < (node x, node y) {
return x.a < y.a;
}
}Dish[200010];
int t;
int n;
ll sum, ans;
int main() {
scanf("%d", &t);
while (t--) {
ans = inf;
sum = 0;
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &Dish[i].a);
for (int i = 1; i <= n; i++) scanf("%d", &Dish[i].b);
sort(Dish + 1, Dish + 1 + n);
for (int i = n; i >= 1; i--) {
ans = min(ans, max((ll)Dish[i].a, sum));
sum += Dish[i].b;
}
ans = min(ans, sum);
printf("%lld
", ans);
}
return 0;
}
D
考虑一个位置至少有几次操作是从最后到它这个位置的?如果 (a_{i-1}<a_i) 那么显然是 (a_{i}-a_{i-1}),那么 (a[i...n]) 这一段数至少减 (a_{i}-a_{i-1}),如果把所有这些要减的加在一起,比某个 (a_x) 大了那么就是NO,否则就是YES。
为什么不用从后往前做一遍?看一下这张图就懂了。
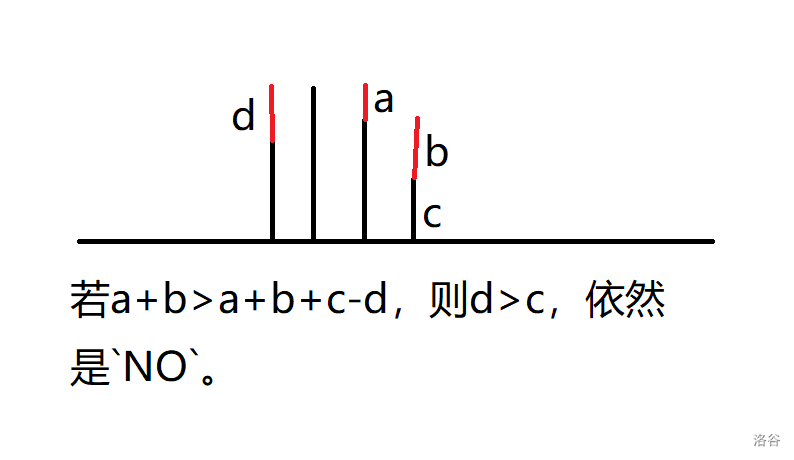
这一类题因为是区间同时减去某数所以有一段的差分数组不变,多往差分上去想。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
int q;
int n;
int a[100010];
int now;
int main() {
scanf("%d", &q);
while (q--) {
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]);
now = 0;
bool ans = true;
for (int i = 1; i < n; i++) {
if (now > a[i]) {
ans = false;
break;
}
if (a[i] < a[i + 1]) now += a[i + 1] - a[i];
}
if (now > a[n]) ans = false;
if (ans) puts("YES");
else puts("NO");
}
return 0;
}
E
挺水的一题,可惜赛时不知道F更水,然后花了挺多时间搞这题害的最后没时间写F了/kk/kk/kk。
看到这道题让你实现的就是跳到字典序比当前大一的排列上,而字典序最大为 (2 imes 10^{10}),这对于排列的个数来说其实是很小的。保守点说,排列变化的肯定是最后 (20) 个数。那么对于前 (n-20) 个数维护一个前缀和,后 (20) 个数暴力统计就可以做第一问。对于第二个操作,根据排名求排列有个逆康托展开的算法,具体就是挨个确定每个位置是什么数,如果暴力做的话复杂度上限是 (20^3),然而到不了所以这题可以过,如果要追求效率的话可以做到 (20 imes log^2{20}) 或者 (20 imes log{20}).
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int n, q;
ll now = 1;
ll a[200010], cnt[200010];
bool vis[200010];
ll ans;
int main() {
scanf("%d%d", &n, &q);
for (int i = 1; i <= n; i++) a[i] = i, cnt[i] = a[i] + cnt[i - 1];
while (q--) {
int opt, l, r;
scanf("%d", &opt);
if (opt == 1) {
scanf("%d%d", &l, &r);
ans = 0;
if (n > 20) {
if (l < n - 20 && r >= n - 20) {
ans = cnt[n - 21] - cnt[l - 1];
l = n - 20;
for (int i = l; i <= r; i++) {
ans += a[i];
}
} else if (r < n - 20) {
ans = cnt[r] - cnt[l - 1];
} else {
for (int i = l; i <= r; i++) {
ans += a[i];
}
}
} else {
for (int i = l; i <= r; i++) {
ans += a[i];
}
}
printf("%lld
", ans);
} else {
scanf("%d", &l);
now += l;
ll tmp = now;
ll cur = 1;
int pos;
for (pos = n; pos; pos--) {
if (cur >= now) {
break;
}
cur *= (n - pos + 1);
}
for (int i = pos + 1; i <= n; i++) vis[i] = false;
for (int i = pos + 1; i <= n; i++) {
cur /= (n - i + 1);
for (int j = pos + 1; j <= n; j++) {
if (vis[j]) continue;
ll num = 0;
for (int k = pos + 1; k < i; k++) {
if (a[k] < j) {
num++;
}
}
if (cur * (j - pos - num) >= now) {
now -= cur * (j - pos - num - 1);
a[i] = j;
vis[j] = true;
break;
}
}
}
now = tmp;
}
}
return 0;
}
F
首先我们发现要想某个数加入 (b) 就得把它旁边两个中的一个删掉,然后这是两种情况,所以每次操作最多两种情况,答案肯定是 (2) 的倍数。考虑什么情况不是 (2)?记录每个数在 (a) 中出现的位置 (p),如果 (a_{p_{b_i}+1}) 是在 (b) 中 (i) 的后面出现的数,那么一定不能删。如果 (p_{b_i}=n) 那么后面的数也没得删,前面同理。于是我们从后往前推,对于每个 (b_i) 打上标记,这样就可以 (O(1)) 判断了。
为什么只有一开始的位置才影响答案?因为如果想要把旁边的删掉一定要把你这个位置的删掉,而你这个位置在之前有不能删,所以旁边的一定还存在。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 998244353;
const int inf = 0x3f3f3f3f;
int T;
int n, m;
int a[200010], b[200010], pos[200010];
bool vis[200010];
ll ans;
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) scanf("%d", &a[i]), pos[a[i]] = i, vis[i] = false;
for (int i = 1; i <= m; i++) scanf("%d", &b[i]);
ans = 1;
for (int i = m; i >= 1; i--) {
ll cur = 2;
if (pos[b[i]] == 1 || vis[a[pos[b[i]] - 1]]) cur--;
if (pos[b[i]] == n || vis[a[pos[b[i]] + 1]]) cur--;
ans = (ans * cur) % mod;
vis[b[i]] = true;
}
printf("%lld
", ans);
}
return 0;
}
总结一下这场比赛,前3题很水随便过,但是B花的时间还是多了点,以后要做到前两题15min以内做完(除非是公认的毒瘤场)。然后这个D的套路一开始竟然没有直接想到,这种区间加减的一般都要考虑差分,我还是太菜了。E应该算是马上就想到了只有最后几个会变,但是逆康托展开打了好久,还是知识点不熟悉,并且犯了低级错误wa了两发,打代码时还是不能太急。最后这个F应该比E水但是考试时没看榜导致还是先去做了E,最后没时间打F了。。。然而还是比较套路的,这种一个一个策略的问题其实可以考虑从后往前倒推。大概就这么多吧,我还是太菜了。