这次考试总的来说还算正常发挥,不过因为对算法不熟悉没有很快想出T2最后想出来却没时间调了。
最后得分100+77+100=277,rank2。(不过没AK有点可惜)
刚开始我先把每到题看了一遍,然后T1没太理解,T2没啥思路,于是先去做T3。
T3一看就是道主席树的裸题。
维护一下值和出现次数就行了,我很快就打完了代码,但交上去只有25pts。
当时心态有点炸,仔细检查一下发现是再减去lca的值时没有*2,改了之后轻松A掉了这一题。
然后我再去做T2。
T2想到一个很简单的单次查询$O(n)$的暴力贪心,写完交上去拿了77pts,比期望高27pts,估计是出题人用脚造数据吧。
然后就没有在去看T2了,决定先去搞T1。
此时刚刚过去1/3的时间。
T1描述太过奇怪,我大概又花了20min才看懂,感觉是个贪心。
然后写了个代码交上去只有25pts。写个对拍(这花了我很长时间)发现了一些错误,改了之后交上去就A了。
这是离结束只有30min。
A了这题之后我信心大涨,去看T2。
我突然想到T2说不定可以用倍增去优化之前的暴力(赛后发现我的想法是对的),写了之后有点小问题。
这时离考试结束只有2min了,最后也没改过哪个错误,考试结束才改过来。
赛后发现做出来的人最多的T2我却没做出来,我认为这主要原因是我对某些算法的不熟悉,毕竟我很久没练倍增了。
还有就是花了太久时间取读T1的题意了。
接下来我就来讲一下题解:
T1 游戏公司
原题:AGC004D
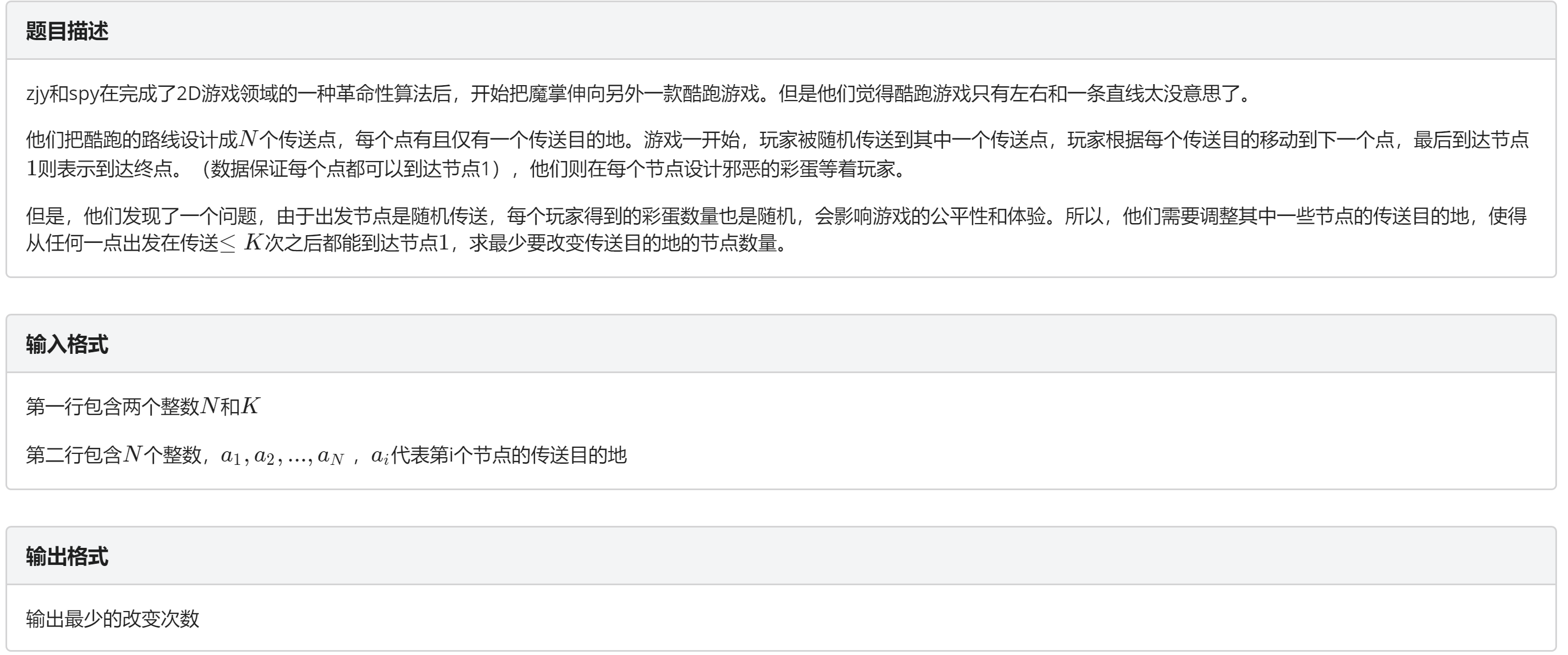
题目描述:
题解:
很容易想到贪心。
首先这个题很毒瘤的是1号节点必须连一条到自己的自环。剩下的结构如果我们把每条边取反可以得到一棵以1为根的树。
然后处理每个节点的深度和可以到达的最大深度,然后从叶节点向上回溯的时候如果某一个节点这个数的差>=k的时候,就得把它连向1,之后它的子树到1的距离都小于等于k了,如果它的父亲即是一号点,则如果这个差值>=k-1时都要连向1.
如果它连向1了一条边,则它的父亲统计最大深度时也不用统计它的子树了。
注意如果1本来没连向自己答案还要加1。
#include <iostream> #include <cstdio> #include <algorithm> #include <vector> #include <queue> using namespace std; const int N = 100010; struct node{ int pre, to; }edge[N << 1]; int head[N], tot; int n, k; int a[N]; int dis[N], mx[N]; int ans; bool vis[N]; void dfs(int x) { for (int i = head[x]; i; i = edge[i].pre) { int y = edge[i].to; dis[y] = dis[x] + 1; dfs(y); mx[x] = max(mx[x], mx[y]); } mx[x] = max(mx[x], dis[x]); if (x != 1) { if (mx[x] - dis[x] >= k) mx[x] = 0, ans++; if (mx[x] - dis[x] == k - 1 && a[x] != 1) mx[x] = 0, ans++; } } void add(int u, int v) { edge[++tot] = node{head[u], v}; head[u] = tot; } int main() { scanf("%d%d", &n, &k); for (int i = 1; i <= n; i++) { scanf("%d", &a[i]); if (i == 1) { if (a[i] != 1) ans++; } else { add(a[i], i); } } dfs(1); cout << ans; return 0; }
T2 偷渡者xibo
原题:ARC060C
题目描述

题解
考虑暴力贪心,其实就是求它一天最远能走到哪,而这样做的复杂度是$O(n)$的显然不行(有77pts)。
考虑优化,如果二分找到一天最远能走到哪,复杂度数$O(ans imes log{n})$的,最坏情况还不如上一个暴力(亲测只有66pts)。
考虑每次不止走一天,很容易想到倍增优化:dp[i][j]代表从i走$2^j$天最远能走多远,有dp[i][j]=dp[dp[i][j-1]][j-1]
然后就很简单了。
#include <iostream> #include <cstdio> #include <cstring> using namespace std; const int N = 1000010; int n; int a[N]; int L, q, ans, lst; int dp[N][21]; int pow[21]; int main() { memset(dp, 0x3f, sizeof(dp)); scanf("%d", &n); for (int i = 1; i <= n; i++) scanf("%d", &a[i]); scanf("%d", &L); scanf("%d", &q); pow[0] = 1; for (int i = 1; i <= n; i++) { pow[i] = pow[i - 1] << 1; lst = max(i, lst); for (int j = lst + 1; j <= n; j++) { if (a[j] - a[i] <= L) { lst = j; } } dp[i][0] = lst; } for (int j = 1; j <= 20; j++) { for (int i = 1; i <= n; i++) { if (dp[i][j - 1] < 0x3f3f3f3f) dp[i][j] = dp[dp[i][j - 1]][j - 1]; } } while (q--) { int x, y; scanf("%d%d", &x, &y); if (x > y) swap(x, y); ans = 0; for (int i = 20; i >= 0; i--) { if (dp[x][i] < y) { x = dp[x][i]; ans += pow[i]; } } printf("%d ", ans + 1); } return 0; }
T3 五彩树
原题:ABC133F

主席树裸题,不讲了。
#include <iostream> #include <cstdio> using namespace std; typedef long long ll; const ll N = 100010; struct Segment{ ll cnt, val, lson, rson;//出现次数,值 }tr[N * 20]; ll rt[N]; struct node{ ll pre, to, col, val; }edge[N << 1]; ll head[N], tot; ll n, q; ll dis[N], dep[N], fa[N], son[N], sz[N], bl[N]; void dfs1(ll x) { sz[x] = 1; for (ll i = head[x]; i; i = edge[i].pre) { ll y = edge[i].to; if (y == fa[x]) continue; dep[y] = dep[x] + 1; dis[y] = dis[x] + edge[i].val; fa[y] = x; dfs1(y); sz[x] += sz[y]; if (sz[y] > sz[son[x]]) { son[x] = y; } } } void dfs2(ll x, ll chain) { bl[x] = chain; if (son[x]) dfs2(son[x], chain); for (ll i = head[x]; i; i = edge[i].pre) { ll y = edge[i].to; if (y == fa[x] || y == son[x]) continue; dfs2(y, y); } } ll LCA(ll u, ll v) { while (bl[u] != bl[v]) { if (dep[bl[u]] < dep[bl[v]]) swap(u, v); u = fa[bl[u]]; } return dep[u] < dep[v] ? u : v; } void push_up(ll cur) { tr[cur].cnt = tr[tr[cur].lson].cnt + tr[tr[cur].rson].cnt; tr[cur].val = tr[tr[cur].lson].val + tr[tr[cur].rson].val; } void ins(ll &cur, ll pre, ll l, ll r, ll pos, ll v) { cur = ++tot; tr[cur] = tr[pre]; if (l == r) { tr[cur].cnt++; tr[cur].val += v; return; } ll mid = (l + r) >> 1; if (pos <= mid) ins(tr[cur].lson, tr[pre].lson, l, mid, pos, v); else ins(tr[cur].rson, tr[pre].rson, mid + 1, r, pos, v); push_up(cur); } ll ask_val(ll cur, ll l, ll r, ll pos) { if (l == r) return tr[cur].val; ll mid = (l + r) >> 1; if (pos <= mid) return ask_val(tr[cur].lson, l, mid, pos); else return ask_val(tr[cur].rson, mid + 1, r, pos); } ll ask_cnt(ll cur, ll l, ll r, ll pos) { if (l == r) return tr[cur].cnt; ll mid = (l + r) >> 1; if (pos <= mid) return ask_cnt(tr[cur].lson, l, mid, pos); else return ask_cnt(tr[cur].rson, mid + 1, r, pos); } void solve(ll x) { for (ll i = head[x]; i; i = edge[i].pre) { ll y = edge[i].to; if (y == fa[x]) continue; ins(rt[y], rt[x], 1, n, edge[i].col, edge[i].val); solve(y); } } void add(ll u, ll v, ll c, ll d) { edge[++tot] = node{head[u], v, c, d}; head[u] = tot; } int main() { scanf("%lld%lld", &n, &q); for (ll i = 1, u, v, c, d; i < n; i++) { scanf("%lld%lld%lld%lld", &u, &v, &c, &d); add(u, v, c, d); add(v, u, c, d); } dfs1(1); dfs2(1, 1); solve(1); while (q--) { ll x, y, u, v; scanf("%lld%lld%lld%lld", &x, &y, &u, &v); ll lca = LCA(u, v); ll value = ask_val(rt[u], 1, n, x) + ask_val(rt[v], 1, n, x) - 2 * ask_val(rt[lca], 1, n, x); ll cnt = ask_cnt(rt[u], 1, n, x) + ask_cnt(rt[v], 1, n, x) - 2 * ask_cnt(rt[lca], 1, n, x); printf("%lld ", dis[u] + dis[v] - 2 * dis[lca] - value + cnt * y); } return 0; }