问题描述
根据输入的正整数n ,输出一个米字形图案。米字形由一个(2n-1)*(2n-1)的矩阵组成,矩阵包含从大写A开始的n个字母
例如:n=3时,包含A,B,C;n=4时,包含A,B,C,D。
矩阵的正中间为n个字母中字典序最大的那个,从这个字母开始,沿着西北、正北、东北、正西、正东、西南、正南、东南八个方向各有一条由大写字母组成的直线。并且直线上的字母按字典序依次减小,直到大写字母A。
矩阵的其它位置用英文句号.填充。
样例输入一
3
样例输出一
A.A.A
.BBB.
ABCBA
.BBB.
A.A.A
样例输入二
4
样例输出二
A..A..A
.B.B.B.
..CCC..
ABCDCBA
..CCC..
.B.B.B.
A..A..A
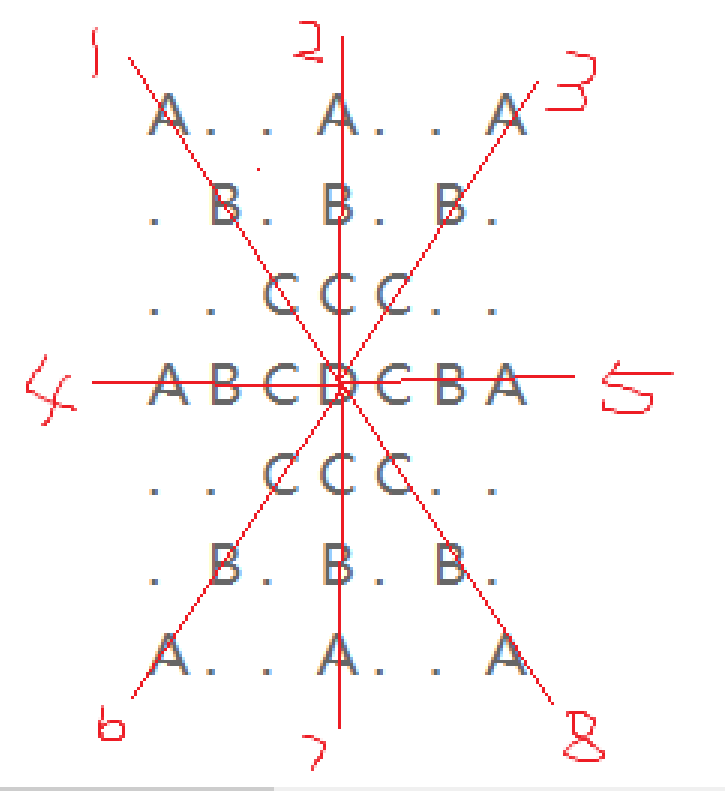
思路:8个for循环,每个for循环控制一个方向。可以先把8个for循环全部注释掉,然后把for循环1放出来,
运行一下,再把for循环1和2放出来,运行一下,一直到8个全放出来,方便理解。摘自这里
可以联想到刚学c语言for循环时的模拟题
#include <bits/stdc++.h> using namespace std; char g[60][60]; int main() { memset(g, '.', sizeof g); int n; cin >> n; for (int i = 0; i < n; i ++ ) // 1方向 g[i][i] = 'A' + i; for (int i = 0; i < n; i ++ ) // 2方向 g[i][n - 1] = 'A' + i; for (int i = 0, j = 2 * n - 2; i < n; j -- , i ++ ) // 3方向 g[i][j] = 'A' + i; for (int i = 0; i < n; i ++ ) // 4方向 g[n - 1][i] = 'A' + i; for (int i = 0, j = 2 * n - 2; i < n; j -- , i ++ ) // 5方向 g[n - 1][j] = 'A' + i; for (int i = 0, j = 2 * n - 2; i < n; j -- , i ++ ) // 6方向 g[j][i] = 'A' + i; for (int i = 0, j = 2 * n - 2; i < n; j -- , i ++ ) // 7方向 g[j][n - 1] = 'A' + i; for (int i = 0, j = 2 * n - 2; i < n; j -- , i ++ ) // 8方向 g[j][j] = 'A' + i; for (int i = 0; i < 2 * n - 1; i++) { //输出 for (int j = 0; j < 2 * n - 1; j++) { cout << g[i][j]; } cout << endl; } return 0; }