试题 算法训练 小生物的逃逸

问题描述

　　空间中有n个球，这些球不相交也不相切。有m个可以视为质点的小生物，可能在某些球内，也可能在所有球之外，但不会在球面上。问这些生物从原来的地方逃逸到所有球外面的空间，至少要经过多少层球面。

输入格式

　　第一行两个数n、m：表示球的数量和小生物的数量；
　　接下来n行每行四个整数Xi、Yi、Zi和Ri：表示一个球的三维坐标和半径；
　　接下来m行每行三个整数Xi、Yi、Zi：表示一个生物的坐标。

输出格式

　　一行m个数：表示每个小生物逃逸时至少经过的球面数。

样例输入

　　2 2
　　0 0 0 2
　　0 0 0 4
　　0 0 1
　　0 0 3

样例输出

　　2 1

数据规模和约定

　　1<=n、m<=100，|Xi|、|Yi|、|Zi|<=10000，1<=Ri<=10000；
　　数据保证所有球严格不接触，小生物都不在球面上。

 

思路：一道非常简单的题 重点是与数学之间的联系 经验++ 下次就会写了

　　二维：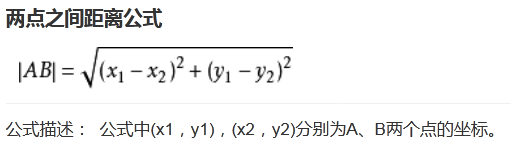

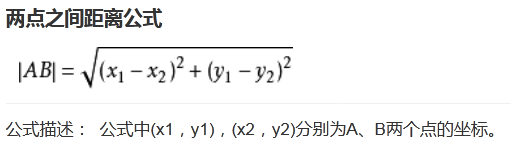
　   三维：

#include <iostream>
#include <cstring>
#include <cmath>
#include <algorithm>

using namespace std;

const int N = 110;

int n, m;
int n_x[N], n_y[N], n_z[N], R[N]; // 球坐标
int m_x[N], m_y[N], m_z[N]; // 生物坐标

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
    {
        cin >> n_x[i] >> n_y[i] >> n_z[i] >> R[i];
    }
    for (int i = 0; i < m; i ++ )
    {
        cin >> m_x[i] >> m_y[i] >> m_z[i];
    }
    for (int i = 0; i < m; i ++ )
    {
        int ans = 0;
        for (int j = 0; j < n; j ++ )
        {
            int x, y, z;
            x = abs(m_x[i] - n_x[j]);
            y = abs(m_y[i] - n_y[j]);
            z = abs(m_z[i] - n_z[j]);
            if (sqrt(x * x + y * y + z * z) < R[j])
            {
                ans ++ ;
            }
        }
        cout << ans << ' ';
    }
    return 0;
}