试题 算法训练 数字游戏

问题描述

　　给定一个1～N的排列a[i]，每次将相邻两个数相加，得到新序列，再对新序列重复这样的操作，显然每次得到的序列都比上一次的序列长度少1，最终只剩一个数字。
　　例如:
　　3 1 2 4
　　4 3 6
　　7 9
　　16
　　现在如果知道N和最后得到的数字sum，请求出最初序列a[i]，为1～N的一个排列。若有多种答案，则输出字典序最小的那一个。数据保证有解。

输入格式

　　第1行为两个正整数n，sum

输出格式

　　一个1～N的一个排列

样例输入

　　4 16

样例输出

　　3 1 2 4

数据规模和约定

　　0<n<=10

 

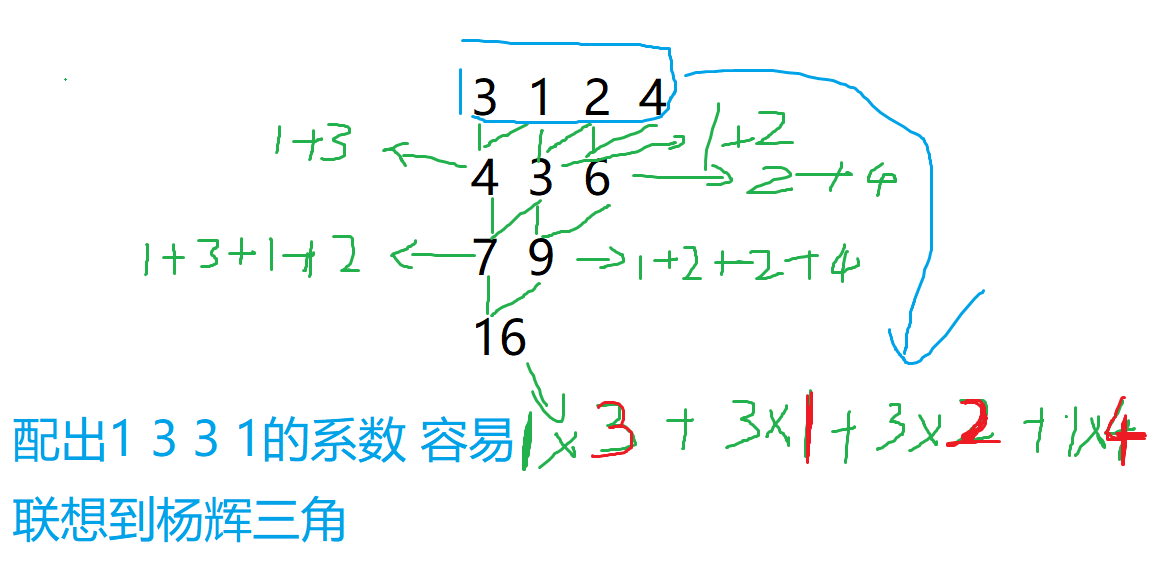
思路1：带有技巧的搜索 先由数据找规律 可联想到杨辉三角 进行打表 然后暴搜

          

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 15;

int n, sum;
int y[N][N], a[N]; // y数组杨辉三角打表 a数组记录路径
bool vis[N];

void dfs(int cur, int s) // cur当前第几个数 s表示总数
{
    if (cur > n)
    {
        if (s == sum)
        {
            for (int i = 1; i <= n; i ++ ) cout << a[i] << ' ';
            exit(0);
        }
    }
    for (int i = 1; i <= n; i ++ )
    {
        if (!vis[i])
        {
            a[cur] = i;
            vis[i] = true;
            dfs(cur + 1, s + i * y[n][cur]); // s + 当前数 * 上图分析的杨辉三角系数
            vis[i] = false;                  // 为什么行是n 因为仔细推发现   
        }                                    // 图中的例题系数 1 3 3 1 正好对应杨辉三角第4行
    }                                        // 即第n行
}

int main()
{
    cin >> n >> sum;
    
    // 杨辉三角 打表
    y[1][1] = 1;
    for (int i = 1; i <= 13; i ++ )
        y[i][1] = 1, y[i][i] = 1;
    for (int i = 3; i <= 13; i ++ )
        for (int j = 1; j <= i; j ++ )
            y[i][j] = y[i - 1][j] + y[i - 1][j - 1];
    
    dfs(1, 0);
    return 0;
}

思路2：全排列思想 无脑做就完事了

#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
using namespace std;

typedef long long LL;

const int N = 15;

int n, sum;
int a[N];

int main()
{
    cin >> n >> sum;
    for (int i = 1; i <= n; i ++ ) a[i] = i;
    do
    {
        int b[n][n];
        memset(b, 0, sizeof b);
        for (int i = 1; i <= n; i ++ ) b[1][i] = a[i];
        for (int i = 2; i <= n; i ++ )
            for (int j = 1; j <= n - i + 1; j ++ )
            　　b[i][j] = b[i - 1][j] + b[i - 1][j + 1];
        if (b[n][1] == sum)
        {
            for (int i = 1; i <= n; i ++ ) cout << a[i] << ' ';
            break;
        }
    } while (next_permutation(a + 1, a + n + 1));
    return 0;
}