省选模拟赛 爬山法

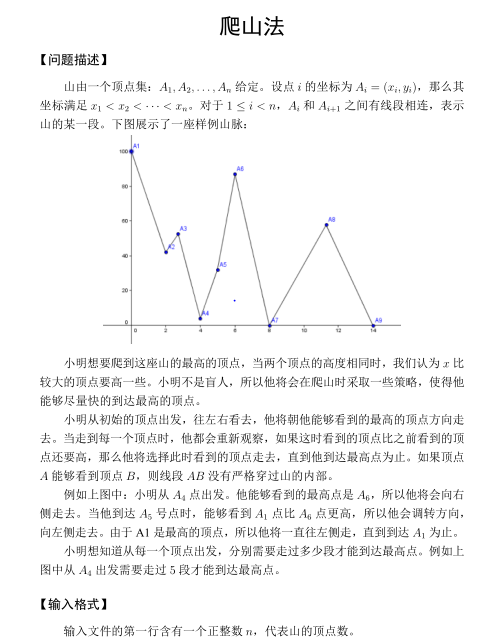
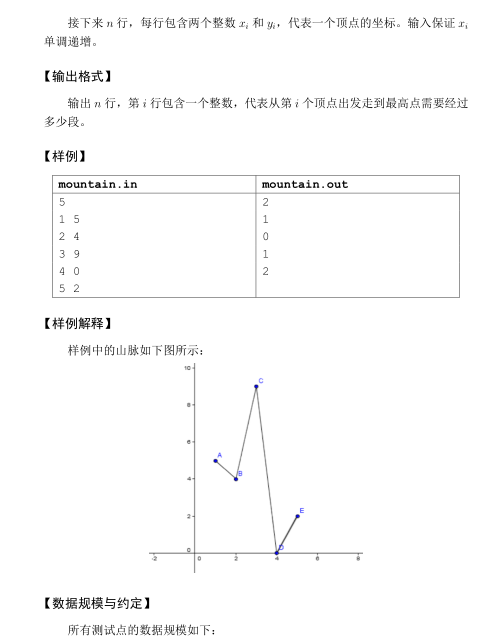
分析：写这题快写吐了......

　　　这道题的思路其实很容易想到：处理出每个点往左往右分别能看到哪. 然后以每个点为起点，照着题目说的那样记忆化搜索一下就好了,用st表处理出转向的情况.

　　　怎么预处理呢？实际上就是维护了一个上凸壳，仿照凸包的维护方法即可. st表不再存储值，而是对应下标.

　　　下面说说我debug了一晚上的错误： 我一直以为如果要从点i到点pos,只需要用st表求出[pos,i]中的点能看到的点的最大高度即可.

那么这个点就是要转向的点. 如果它和pos是同一个点也没关系，相当于不转向嘛.  

　　　第一次尝试：忽略了一种情况. 如果这几个点能看到的点的最大高度分别是5 5 5,st表求出来的是第3个，如果我要从左往右走，实际上需要的是第1个. 这告诉我往左走和往右走的st表应该是不同的？于是写了两个st表.

　　　第二次尝试：st表改过来了,但是tm的死循环...... debug了半天才发现查st表得到的值可能正好为i,那么就会一直在原地不动.

　　　第三次尝试：对拍了一些小数据，基本上都是对的，正当我准备去提交的时候，拍错了一组......然后我把数据改大点，发现每组都错......要命的是，每组数据中只会错一两处，分布还特别分散！于是我找了几组错的小数据，一点点地缩小范围. 发现我的findl函数写错了（从i往左走到pos,中途经过的哪个点的能看到的点的高度最大）.为什么呢？因为我臆想天开！我以为直接查st表中的最大值就好了.题目中说的是要求能看到的点的最大高度＞目标点的高度. naive! 于是二分找一下就好了？

　　　第四次尝试：尼玛怎么又错了.开始只分析findl函数，经过我严密的手算,将程序的中间变量都输出出来后，发现我求的还不是题目要求的.我每次st表查出来的是当前点的最大高度，而不是当前点能看到的点的最大高度. 外面套一层数组就好了......

　　　第五次尝试：跑过了大数据，欣喜地去交，发现只有70分......好像会爆long long? woc,还真是！ 算叉积的时候会爆. 改一下就好了

　　　第六次尝试：第6个点至今还WA着在.,这让我怎么查.（弃）.

　　　　血的教训：一定要按照题目要求来，不要自己想着什么就是什么.

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const ll maxn = 200010;
ll n,fl[maxn],fr[maxn],maxx,cur,top,sta[maxn],mx[maxn],choose[maxn],f[maxn],fa1[maxn][20],fa2[maxn][20],d[maxn];
ll head[maxn],to[maxn],nextt[maxn],tot = 1;

struct node
{
    ll x,y;
} e[maxn];

bool operator>(const node &a,const node &b)
{
    if(a.y==b.y)
        return a.x>b.x;
    else return a.y>b.y;
}

void add(ll x,ll y)
{
    to[tot] = y;
    nextt[tot] = head[x];
    head[x] = tot++;
}

node sub(node a,node b)
{
    node temp;
    temp.x = a.x - b.x;
    temp.y = a.y - b.y;
    return temp;
}

ll det(node a,node b)
{
    return a.x * b.y - a.y * b.x;
}

void preleft()
{
    fl[1] = 1;
    sta[++top] = 1;
    for (ll i = 2; i <= n; i++)
    {
        while (top > 1&& det(sub(e[sta[top]],e[sta[top - 1]]),sub(e[i],e[sta[top]])) >= 0)
            top--;
        fl[i] = sta[top];
        sta[++top] = i;
    }
}

void preright()
{
    top = 0;
    fr[n] = n;
    sta[++top] = n;
    for (ll i = n - 1; i >= 1; i--)
    {
        while (top > 1&& det(sub(e[sta[top]],e[sta[top - 1]]),sub(e[i],e[sta[top]])) <= 0)
            top--;
        fr[i] = sta[top];
        sta[++top] = i;
    }
}

void st1_pre()
{
    for (ll j = 1; j <= 19; j++)
        for (ll i = 1; i + (1 << j) - 1 <= n; i++)
        {
            if (mx[fa1[i][j - 1]] > mx[fa1[i + (1 << (j - 1))][j - 1]])
                fa1[i][j] = fa1[i][j - 1];
            else
                fa1[i][j] = fa1[i + (1 << (j - 1))][j - 1];
        }
}

ll query1(ll l,ll r)
{
    ll t = (ll)((log(r - l + 1)) / log(2.0));
    if (mx[fa1[l][t]] > mx[fa1[r - (1 << t) + 1][t]])
        return fa1[l][t];
    return fa1[r - (1 << t) + 1][t];
}

ll findr(ll st,ll ed)
{
    ll l = st,r = ed,ans = ed;
    while (l <= r)
    {
        ll mid = (l + r) >> 1;
        if (e[choose[query1(l,mid)]] > e[ed])
        {
            ans = mid;
            r = mid - 1;
        }
        else
            l = mid + 1;
    }
    return ans;
}

ll findl(ll st,ll ed)
{
    ll l = st,r = ed;
    ll ans = l;
    while (l <= r)
    {
        ll mid = (l + r) >> 1;
        if (e[choose[query1(mid,r)]] > e[st])
        {
            ans = mid;
            l = mid + 1;
        }
        else
            r = mid - 1;
    }
    return ans;
}

ll dfs(ll x)
{
    if (f[x] != -1)
        return f[x];
    if (x == cur)
        return f[x] = 0;
    if (choose[x] < x)
    {
        ll temp = findl(choose[x],x);
        return f[x] = x - temp + dfs(temp);
    }
    else
    {
        ll temp = findr(x,choose[x]);
        return f[x] = temp - x + dfs(temp);
    }
}

int main()
{
    memset(f,-1,sizeof(f));
    scanf("%lld",&n);
    for (ll i = 1; i <= n; i++)
    {
        scanf("%lld%lld",&e[i].x,&e[i].y);
        if (e[i].y >= maxx)
        {
            maxx = e[i].y;
            cur = i;
        }
    }
    preleft();
    preright();
    fl[cur] = fr[cur] = cur;
    for (ll i = 1; i <= n; i++)
    {
        mx[i] = max(e[fl[i]].y,e[fr[i]].y);
        if (e[fl[i]].y > e[fr[i]].y)
            choose[i] = fl[i];
        else
            choose[i] = fr[i];
        fa1[i][0] = i;
        fa2[i][0] = i;
    }
    mx[cur] = 0x7fffffff;
    st1_pre();
    st2_pre();
    for (ll i = 1; i <= n; i++)
        printf("%lld
",dfs(i));

    return 0;
}