Codeforces 937.D Sleepy Game

D. Sleepy Game

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Petya and Vasya arranged a game. The game runs by the following rules. Players have a directed graph consisting of n vertices and medges. One of the vertices contains a chip. Initially the chip is located at vertex s. Players take turns moving the chip along some edge of the graph. Petya goes first. Player who can't move the chip loses. If the game lasts for 106 turns the draw is announced.

Vasya was performing big laboratory work in "Spelling and parts of speech" at night before the game, so he fell asleep at the very beginning of the game. Petya decided to take the advantage of this situation and make both Petya's and Vasya's moves.

Your task is to help Petya find out if he can win the game or at least draw a tie.

Input

The first line of input contain two integers n and m — the number of vertices and the number of edges in the graph (2 ≤ n ≤ 105, 0 ≤ m ≤ 2·105).

The next n lines contain the information about edges of the graph. i-th line (1 ≤ i ≤ n) contains nonnegative integer ci — number of vertices such that there is an edge from i to these vertices and ci distinct integers ai, j — indices of these vertices (1 ≤ ai, j ≤ n, ai, j ≠ i).

It is guaranteed that the total sum of ci equals to m.

The next line contains index of vertex s — the initial position of the chip (1 ≤ s ≤ n).

Output

If Petya can win print «Win» in the first line. In the next line print numbers v1, v2, ..., vk (1 ≤ k ≤ 106) — the sequence of vertices Petya should visit for the winning. Vertex v1 should coincide with s. For i = 1... k - 1 there should be an edge from vi to vi + 1 in the graph. There must be no possible move from vertex vk. The sequence should be such that Petya wins the game.

If Petya can't win but can draw a tie, print «Draw» in the only line. Otherwise print «Lose».

Examples

input

Copy

5 6
2 2 3
2 4 5
1 4
1 5
0
1

output

Win
1 2 4 5 

input

Copy

3 2
1 3
1 1
0
2

output

Lose

input

Copy

2 2
1 2
1 1
1

output

Draw

Note

In the first example the graph is the following:

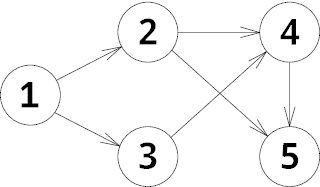
Initially the chip is located at vertex 1. In the first move Petya moves the chip to vertex 2, after that he moves it to vertex 4 for Vasya. After that he moves to vertex 5. Now it is Vasya's turn and there is no possible move, so Petya wins.

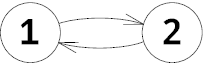
In the second example the graph is the following:

Initially the chip is located at vertex 2. The only possible Petya's move is to go to vertex 1. After that he has to go to 3 for Vasya. Now it's Petya's turn but he has no possible move, so Petya loses.

In the third example the graph is the following:

Petya can't win, but he can move along the cycle, so the players will draw a tie.

题目大意：在一个有向图上，从起点出发，先手走一步，后手在前者的基础上再走一步，不能走的人算输.  现在你既操控了先手，又操控了后手，问你能不能让先手赢，如果不行能不能让这个游戏一直进行下去？

分析：最后走到的点肯定是出度为0的点.我一开始的想法是从起点出发bfs,如果走到一个出度为0的点并且路径的长度为奇数，则能赢.否则就看图中是否存在环，如果有环并且和起点连通，那么游戏就能一直进行下去了.否则就会输掉.

　　　这个想法有一种情况没有考虑到：走到出度为0的点并且路径长度为偶数，按照之前的判断应该是不行的，但是如果这个路径上套一个奇环就不一样了，可以在奇环上走一圈那么路径长度就为奇数了. 直接统计点数为奇数的环不是很容易，需要换一个思路.

　　　从起点开始dfs,记录走到当前点的路径的奇偶性.vis数组记录走到点u并且经过路径的奇偶性为p这个状态是否访问过.枚举u的下一个点v,那么走到v的话奇偶性就变成了p ^ 1 = q.如果vis[v][q]没有被标记，就走到v,记录路径. 如果被标记了1，说明有环，游戏能够一直下去.如果u的所有后继点都被访问完了，就将vis[u][p]标记为2.

　　　为什么还要让标记为2呢？考虑下面一种情况：

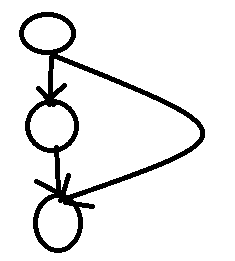，对于最下面的一个点，先走左边的路径，那么它被标记为了1，再从右边走，发现它已经被标记为了1，就会认为这是一个环！如果打上2标记就不会出现这种情况.

　　　get到了找奇环的新技巧，找环问题要考虑好vis数组到底会不会用到标记2!

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;
const int maxn = 1000010;
int n,m,head[maxn],to[maxn],nextt[maxn],tot = 1,s;
int vis[maxn][3],pre[maxn][3],du[maxn],ansnode,cnt,anss[maxn];
bool flag = false,can = false;

void add(int x,int y)
{
    to[tot] = y;
    nextt[tot] = head[x];
    head[x] = tot++;
}

bool dfs(int u,int p)
{
    vis[u][p] = 1;
    int q = p ^ 1;
    for (int i = head[u];i;i = nextt[i])
    {
        int v = to[i];
        if (!vis[v][q])
        {
            pre[v][q] = u;
            if (dfs(v,q))
                return true;
        }
        else
            if (vis[v][q] == 1)
                flag = true;
    }
    if (du[u] == 0 && p == 1)
    {
        can = 1;
        ansnode = u;
        return true;
    }
    vis[u][p] = 2;
    return false;
}

int main()
{
    scanf("%d%d",&n,&m);
    for (int i = 1; i <= n; i++)
    {
        int num;
        scanf("%d",&num);
        du[i] = num;
        for (int j = 1; j <= num; j++)
        {
            int x;
            scanf("%d",&x);
            add(i,x);
        }
    }
    scanf("%d",&s);
    if (dfs(s,0))
    {
        puts("Win");
        int x = 1;
        while (ansnode != 0)
        {
            anss[++cnt] = ansnode;
            ansnode = pre[ansnode][x];
            x ^= 1;
        }
        for (int i = cnt; i >= 1; i--)
            printf("%d ",anss[i]);
    }
    else
        if (flag)
            puts("Draw");
    else
        puts("Lose");

    return 0;
}