bzoj1486 [HNOI2009]最小圈

1486: [HNOI2009]最小圈

Time Limit: 10 Sec  Memory Limit: 64 MB
Submit: 2723  Solved: 1310
[Submit][Status][Discuss]

分析：分数规划.

　　　其实就是最小化，令其 = ans,那么化简一下就是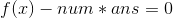：.如果ans过大，则左边会小于0，如果过小，则左边会大于0.事实上这就是一个二分的过程.将ans看作平均权值.代到式子中，那么式子表示的意义就是将所有边权减掉ans后是否存在负环.

这里用dfs版的spfa特判一下就好了.

　　　我的这份代码还有许多可以优化的地方.在实数范围内二分不仅可以比较精度，还可以设定一个循环次数，通常后者更好一些.

每次选取一个点做spfa并不需要清空vis和d数组.事实上不优化这两个地方也能过.

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const double eps = 1e-9,inf = 1000000000000000000.0;
const int maxn = 10010;

struct node
{
    int x,y;
    double len;
} e[maxn];

int n,m,head[maxn],to[maxn],nextt[maxn],tot = 1,vis[maxn];
double ans,w[maxn],d[maxn];
bool flag = false;

void add(int x,int y,double z)
{
    w[tot] = z;
    to[tot] = y;
    nextt[tot] = head[x];
    head[x] = tot++;
}

void spfa(int u)
{
    vis[u] = 1;
    for (int i = head[u]; i; i = nextt[i])
    {
        int v = to[i];
        if (d[v] > d[u] + w[i])
        {
            if (vis[v])
            {
                flag = true;
                break;
            }
            else
            {
                d[v] = d[u] + w[i];
                spfa(v);
            }
        }
    }
    vis[u] = 0;
}

bool check(double x)
{
    memset(head,0,sizeof(head));
    flag = false;;
    tot = 1;
    for (int i = 1; i <= m; i++)
        add(e[i].x,e[i].y,e[i].len - x);
    for (int i = 1; i <= n; i++)
    {
        memset(vis,0,sizeof(vis));
        memset(d,127/3,sizeof(d));
        d[i] = 0;
        spfa(i);
        if (flag)
            return true;
    }
    return false;
}

int main()
{
    scanf("%d%d",&n,&m);
    for (int i = 1; i <= m; i++)
        scanf("%d%d%lf",&e[i].x,&e[i].y,&e[i].len);
    double l = -10000000,r = 10000000;
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid))
        {
            ans = mid;
            r = mid;
        }
        else
            l = mid;
    }
    printf("%.8lf
",ans);

    return 0;
}