2441: [中山市选2011]小W的问题
Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 487 Solved: 186
[Submit][Status][Discuss]
Description
有一天,小W找了一个笛卡尔坐标系,并在上面选取了N个整点。他发现通过这些整点能够画出很多个“W”出来。具体来说,对于五个不同的点(x1, y1), (x2, y2), (x3, y3), (x4, y4), (x5, y5),如果满足:
·x1 < x2 < x3 < x4 < x5
·y1 > y3 > y2
·y5 > y3 > y4
则称它们构成一个“W”形。
现在,小W想统计“W”形的个数,也就是满足上面条件的五元点组个数。你能帮助他吗?
。
Input
第一行包含一个整数N,表示点的个数。
下面N行每行两个整数,第i+1行为(xi, yi),表示第i个点的坐标。
Output
仅包含一行,为“W”形个数模1 000 000 007的值。
Sample Input
6
1 10
2 1
3 5
4 6
5 1
6 10
1 10
2 1
3 5
4 6
5 1
6 10
Sample Output
3
HINT
对于100%的数据满足N ≤ 200 000,0 ≤ xi ≤ 10^9,0 ≤ yi ≤ 10^9
Source
开始做这道题的时候还是正中午,现在......
这题真的是烦,如果横纵坐标不相等,还好点,现在相等了,直接gg.
两个思路,一是统计下面几种图形的数量:
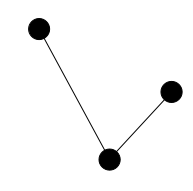
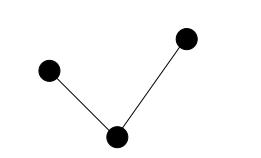
 ,容斥一下就好了.我写了横纵坐标不相等的代码,但是一旦横纵坐标相等就gg.
,容斥一下就好了.我写了横纵坐标不相等的代码,但是一旦横纵坐标相等就gg.
另外的思路是借鉴的网上其他题解的.
结果两份代码都没debug成功QAQ,省选前我会回来填坑的.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; const ll maxn = 200010,mod = 1000000007,inf = 2000000000; struct node { ll x,y,x2,id; }e[maxn]; int n; ll ans1[maxn],ans2[maxn],b[maxn],sum[maxn << 2],L[maxn << 2],R[maxn << 2],tag[maxn << 2],ans,tot; bool cmp(node a,node b) { return a.y < b.y; } bool cmp2(node a,node b) { return a.x < b.x; } void pushup(int o) { sum[o] = sum[o * 2] + sum[o * 2 + 1]; sum[o] %= mod; } void build(int o,int l,int r) { L[o] = l,R[o] = r; sum[o] = tag[o] = 0; if (l == r) return; int mid = (l + r) >> 1; build(o * 2,l,mid); build(o * 2 + 1,mid + 1,r); pushup(o); } void pushdown(int o) { if (tag[o]) { tag[o * 2] += tag[o]; tag[o * 2] %= mod; tag[o * 2 + 1] += tag[o]; tag[o * 2 + 1] %= mod; sum[o * 2] += tag[o] * (R[o * 2] - L[o * 2] + 1) % mod; sum[o * 2 + 1] += tag[o] * (R[o * 2 + 1] - L[o * 2 + 1] + 1) % mod; tag[o] = 0; } } void update(int o,int l,int r,int x,int y,int v) { if (x > y) return; if (x <= l && r <= y) { sum[o] += (r - l + 1) * 1LL * v % mod; sum[o] %= mod; tag[o] += v; tag[o] %= mod; return; } pushdown(o); int mid = (l + r) >> 1; if (x <= mid) update(o * 2,l,mid,x,y,v); if (y > mid) update(o * 2 + 1,mid + 1,r,x,y,v); pushup(o); } void update2(int o,int l,int r,int pos,int v) { if (l == r) { //sum[o] += v; //sum[o] %= mod; //tag[o] += v; //tag[o] %= mod; sum[o] = v; return; } pushdown(o); int mid = (l + r) >> 1; if (pos <= mid) update2(o * 2,l,mid,pos,v); else update2(o * 2 + 1,mid + 1,r,pos,v); pushup(o); } ll query(int o,int l,int r,int x,int y) { if (x > y) return 0; if (x <= l && r <= y) return sum[o]; pushdown(o); ll res = 0; int mid = (l + r) >> 1; if (x <= mid) res += query(o * 2,l,mid,x,y); res %= mod; if (y > mid) res += query(o * 2 + 1,mid + 1,r,x,y); res %= mod; return res; } void solve1() { build(1,1,n); for (int i = 1; i <= n; i++) { int j = i; while (j < n && e[i].y == e[j + 1].y) j++; for (int k = i; k <= j; k++) update(1,1,n,e[k].x2,n,-1); for (int k = i; k <= j; k++) ans1[e[k].id] = query(1,1,n,1,e[k].x - 1); for (int k = i; k <= j; k++) update2(1,1,n,e[k].id,e[k].x - 1); i = j; } } void solve2() { build(1,1,n); for (int i = 1; i <= n; i++) { int j = i; while (j < n && e[i].y == e[j + 1].y) j++; for (int k = i; k <= j; k++) update(1,1,n,1,e[k].x - 1,-1); for (int k = i; k <= j; k++) ans2[e[k].id] = query(1,1,n,e[k].x2,n); for (int k = i; k <= j; k++) update2(1,1,n,e[k].id,n - e[k].x2 + 1); i = j; } } int main() { scanf("%d",&n); for (int i = 1; i <= n; i++) { scanf("%lld%lld",&e[i].x,&e[i].y); b[++tot] = e[i].x; } b[++tot] = inf; sort(b + 1,b + 1 + tot); sort(e + 1,e + 1 + n,cmp2); for (int i = 1; i <= n; i++) { e[i].x2 = upper_bound(b + 1,b + 1 + tot,e[i].x) - b; e[i].x = lower_bound(b + 1,b + 1 + tot,e[i].x) - b; e[i].id = i; } sort(e + 1,e + 1 + n,cmp); solve1(); sort(e + 1,e + 1 + n,cmp); solve2(); /* for (int i = 1; i <= n; i++) { printf("%lld %lld ",ans1[i],ans2[i]); ans += ans1[i] * ans2[i] % mod; ans %= mod; } */ printf("%lld ",ans); return 0; }
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; const ll maxn = 200010,mod = 1000000007,inf = 2000000000; struct node { ll x,y,x2,id; }e[maxn]; ll n; ll ans1[maxn],ans2[maxn],b[maxn],sum[maxn << 2],L[maxn << 2],R[maxn << 2],tag[maxn << 2],ans,tot; bool cmp(node a,node b) { return a.y < b.y; } bool cmp2(node a,node b) { return a.x < b.x; } void pushup(ll o) { sum[o] = sum[o * 2] + sum[o * 2 + 1]; sum[o] %= mod; } void build(ll o,ll l,ll r) { L[o] = l,R[o] = r; sum[o] = tag[o] = 0; if (l == r) return; ll mid = (l + r) >> 1; build(o * 2,l,mid); build(o * 2 + 1,mid + 1,r); pushup(o); } void pushdown(ll o) { if (tag[o]) { tag[o * 2] += tag[o]; tag[o * 2] %= mod; tag[o * 2 + 1] += tag[o]; tag[o * 2 + 1] %= mod; sum[o * 2] += tag[o] * (R[o * 2] - L[o * 2] + 1) % mod; sum[o * 2 + 1] += tag[o] * (R[o * 2 + 1] - L[o * 2 + 1] + 1) % mod; tag[o] = 0; } } void update(ll o,ll l,ll r,ll x,ll y,ll v) { if (x > y) return; if (x <= l && r <= y) { sum[o] += (r - l + 1) * 1LL * v % mod; sum[o] %= mod; tag[o] += v; tag[o] %= mod; return; } pushdown(o); ll mid = (l + r) >> 1; if (x <= mid) update(o * 2,l,mid,x,y,v); if (y > mid) update(o * 2 + 1,mid + 1,r,x,y,v); pushup(o); } void update2(ll o,ll l,ll r,ll pos,ll v) { if (l == r) { sum[o] = v; return; } pushdown(o); ll mid = (l + r) >> 1; if (pos <= mid) update2(o * 2,l,mid,pos,v); else update2(o * 2 + 1,mid + 1,r,pos,v); pushup(o); } ll query(ll o,ll l,ll r,ll x,ll y) { if (x > y) return 0; if (x <= l && r <= y) return sum[o]; pushdown(o); ll res = 0; ll mid = (l + r) >> 1; if (x <= mid) res += query(o * 2,l,mid,x,y); res %= mod; if (y > mid) res += query(o * 2 + 1,mid + 1,r,x,y); res %= mod; return res; } void solve1() { build(1,1,n); for (ll i = 1; i <= n; i++) { ll j = i; while (j < n && e[i].y == e[j + 1].y) j++; for (ll k = i; k <= j; k++) update(1,1,n,e[k].x2,n,-1); for (ll k = i; k <= j; k++) ans1[e[k].id] = query(1,1,n,1,e[k].x - 1); for (ll k = i; k <= j; k++) update2(1,1,n,e[k].id,e[k].x - 1); i = j; } } void solve2() { build(1,1,n); for (ll i = 1; i <= n; i++) { ll j = i; while (j < n && e[i].y == e[j + 1].y) j++; for (ll k = i; k <= j; k++) update(1,1,n,1,e[k].x - 1,-1); for (ll k = i; k <= j; k++) ans2[e[k].id] = query(1,1,n,e[k].x2,n); for (ll k = i; k <= j; k++) update2(1,1,n,e[k].id,n - e[k].x2 + 1); i = j; } } int main() { scanf("%d",&n); for (ll i = 1; i <= n; i++) { scanf("%lld%lld",&e[i].x,&e[i].y); b[++tot] = e[i].x; } b[++tot] = inf; sort(b + 1,b + 1 + tot); sort(e + 1,e + 1 + n,cmp2); for (ll i = 1; i <= n; i++) { e[i].x2 = upper_bound(b + 1,b + 1 + tot,e[i].x) - b; e[i].x = lower_bound(b + 1,b + 1 + tot,e[i].x) - b; e[i].id = i; } sort(e + 1,e + 1 + n,cmp); solve1(); sort(e + 1,e + 1 + n,cmp); solve2(); for (ll i = 1; i <= n; i++) { ans += ans1[i] * ans2[i] % mod; ans %= mod; } printf("%lld ",ans); return 0; }