2154: Crash的数字表格
Time Limit: 20 Sec Memory Limit: 259 MBSubmit: 4549 Solved: 1643
[Submit][Status][Discuss]
Description
今天的数学课上,Crash小朋友学习了最小公倍数(Least Common Multiple)。对于两个正整数a和b,LCM(a, b)表示能同时被a和b整除的最小正整数。例如,LCM(6, 8) = 24。回到家后,Crash还在想着课上学的东西,为了研究最小公倍数,他画了一张N*M的表格。每个格子里写了一个数字,其中第i行第j列的那个格子里写着数为LCM(i, j)。一个4*5的表格如下: 1 2 3 4 5 2 2 6 4 10 3 6 3 12 15 4 4 12 4 20 看着这个表格,Crash想到了很多可以思考的问题。不过他最想解决的问题却是一个十分简单的问题:这个表格中所有数的和是多少。当N和M很大时,Crash就束手无策了,因此他找到了聪明的你用程序帮他解决这个问题。由于最终结果可能会很大,Crash只想知道表格里所有数的和mod 20101009的值。
Input
输入的第一行包含两个正整数,分别表示N和M。
Output
输出一个正整数,表示表格中所有数的和mod 20101009的值。
Sample Input
4 5
Sample Output
122
【数据规模和约定】
100%的数据满足N, M ≤ 10^7。
【数据规模和约定】
100%的数据满足N, M ≤ 10^7。
分析:比较难的一道题,题目要求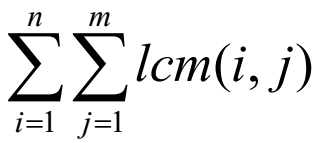 ,其中lcm(i,j) = i*j / gcd(i,j),带入式子中可以得到:
,其中lcm(i,j) = i*j / gcd(i,j),带入式子中可以得到: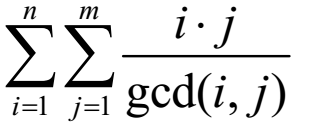 ,枚举i,j是不划算的,设d = gcd(i,j),枚举d,并设F(x,y)表示
,枚举i,j是不划算的,设d = gcd(i,j),枚举d,并设F(x,y)表示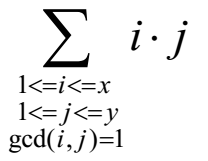 ,gcd(i,j)=1的情况比较好处理,有较为快捷的方法可以得到,那么答案就是
,gcd(i,j)=1的情况比较好处理,有较为快捷的方法可以得到,那么答案就是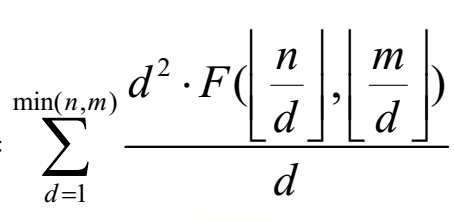 原理就是gcd(i,j) = d ---> gcd(i/d,j/d) = 1,F实际上就是i/d和j/d的乘积和,最后i/d,j/d都要分别乘上d才是ij,约掉一个d,可以得到:
原理就是gcd(i,j) = d ---> gcd(i/d,j/d) = 1,F实际上就是i/d和j/d的乘积和,最后i/d,j/d都要分别乘上d才是ij,约掉一个d,可以得到: .
.
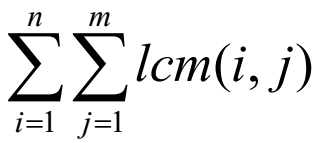 ,其中lcm(i,j) = i*j / gcd(i,j),带入式子中可以得到:
,其中lcm(i,j) = i*j / gcd(i,j),带入式子中可以得到: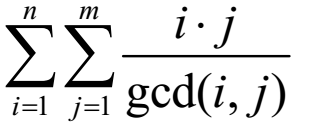 ,枚举i,j是不划算的,设d = gcd(i,j),枚举d,并设F(x,y)表示
,枚举i,j是不划算的,设d = gcd(i,j),枚举d,并设F(x,y)表示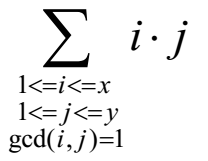 ,gcd(i,j)=1的情况比较好处理,有较为快捷的方法可以得到,那么答案就是
,gcd(i,j)=1的情况比较好处理,有较为快捷的方法可以得到,那么答案就是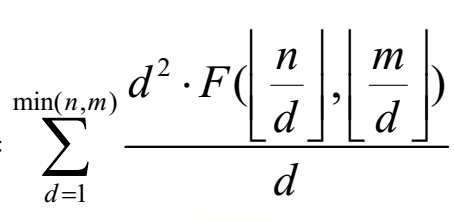 原理就是gcd(i,j) = d ---> gcd(i/d,j/d) = 1,F实际上就是i/d和j/d的乘积和,最后i/d,j/d都要分别乘上d才是ij,约掉一个d,可以得到:
原理就是gcd(i,j) = d ---> gcd(i/d,j/d) = 1,F实际上就是i/d和j/d的乘积和,最后i/d,j/d都要分别乘上d才是ij,约掉一个d,可以得到: .
.
接下来考虑怎么求F函数,当F(x,y)中的x,y固定后,比较麻烦的就是gcd(i,j) = 1的这个限制了,没关系,还是可以沿用上面的思路,将gcd(i,j) = d变成gcd(i/d,j/d) = 1,令sum(x,y) = 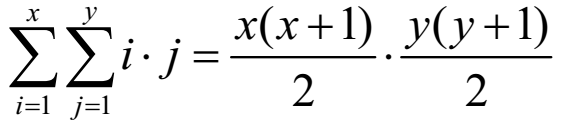 ,那么带入到式子中就可以得到,
,那么带入到式子中就可以得到,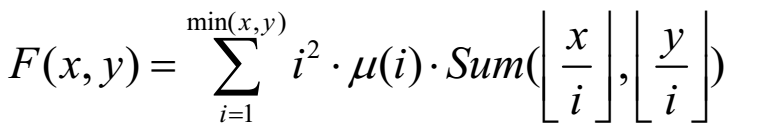 .
.
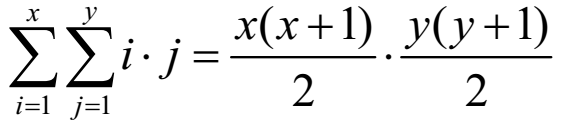 ,那么带入到式子中就可以得到,
,那么带入到式子中就可以得到,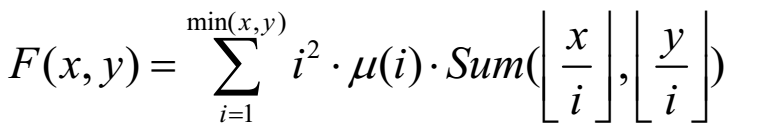 .
. 那么维护两个前缀和,两个式子都可以在根号时间内得到,总的复杂度就是O(n).
这道题我又WA,又T,又MLE的,总结一下原因:MLE是因为数组开的太大了,当空间接近极限的时候能用int就不要用long long,能用bool就不要用int,有一些数组能适当的减小范围,比如筛出来的质数数组,一般比maxn小两个数量级. WA是因为模数的原因,一个函数忘了取模的,结果总是个负数.需要注意的是减法一定要+模数再取模. TLE是因为预处理的上限设定太高了,这道题就一组数据,把min(n,m)当作上限就好了......
#include <cmath> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; const ll maxn = 10000000, mod = 20101009; int prime[3000000], tot, mo[maxn + 10], n, m; bool vis[maxn + 10]; ll sum1[maxn + 10], sum2[maxn + 10]; void init() { mo[1] = 1; for (ll i = 2; i <= min(n,m); i++) { if (!vis[i]) { prime[++tot] = i; mo[i] = -1; } for (ll j = 1; j <= tot; j++) { ll t = prime[j] * i; if (t > min(n,m)) break; vis[t] = 1; if (i % prime[j] == 0) { mo[t] = 0; break; } mo[t] = -mo[i]; } } for (ll i = 1; i <= min(n,m); i++) { sum1[i] = sum1[i - 1] + i; sum2[i] = sum2[i - 1] + i * i * mo[i] % mod; sum1[i] %= mod; sum2[i] %= mod; } } ll sum(ll x, ll y) { return ((x * (x + 1) / 2) % mod) * ((y * (y + 1) / 2) % mod) % mod; } ll F(ll x, ll y) { ll res = 0, last = 0; for (ll i = 1; i <= min(x, y); i = last + 1) { last = min(x / (x / i), y / (y / i)); res += (((sum2[last] - sum2[i - 1] + mod) % mod) * sum(x / i, y / i)) % mod; res %= mod; } return res; } ll solve() { ll res = 0, last = 0; for (ll i = 1; i <= min(n, m); i = last + 1) { last = min(n / (n / i), m / (m / i)); res += (((sum1[last] - sum1[i - 1] + mod) % mod) * F(n / i, m / i)) % mod; res %= mod; } return res; } int main() { scanf("%d%d", &n, &m); init(); printf("%lld ", solve() % mod); return 0; }