问题描
小空正在玩一个叫做捡金币的游戏。游戏在一个被划分成 n行 n列的网格状场地中进行。
每一个格子中都放着若干金币,并且金币的数量会随着时间而不断变化。 小空的任务就是在
网格中移动,拾取尽量多的金币。 并且,小空还有一个特殊技能“闪现”, 能帮助她在网格间
快速移动。
捡金币游戏的具体规则如下:在每一秒开始时,每个网格内都会出现一定数量的金币,
而之前在这格没有被拾取的金币就消失了。在游戏开始时,也就是第 1 秒的开始,小空可以
选择任意一个网格作为起点开始本次游戏,并拾取起点内的金币。之后,在下一秒到来前,
小空可以选择走路移动到与她所在的格子上、下、左、右相邻的一个格子中,或者呆在原地
不动,并在下一秒开始时拾取到她所在的格子中的金币。或者,小空可以选择使用闪现技能,
使用一次闪现时,她先选择上、下、左、右一个方向,之后向该方向移动两格。小空可以在
一秒内使用多次闪现,但不能超过 C 次。在一秒内使用的多次闪现必须向同一个方向移动,
若使用 x 次闪现,便可以向一个方向移动正好 2x 格,并且她也只能在下一秒开始时收集到
连续闪现结束后所在的那一格中的金币。如果在某一秒钟小空使用了闪现,那么她就不能选
择通过走路移动了,反过来也是如此。无论走路或者使用闪现,小空都不能移动到整个场地
之外。整个游戏共进行 T 秒,在第 T 秒开始时,小空将会拾取她所在的格子中的金币,并结
束游戏。 小空在整局游戏内一共只能使用最多 W 次闪现。
举个例子,在如下 3*3 的场地中,游戏共进行 3 秒, 下表列出了 3 秒开始时每一格内的
金币数量。
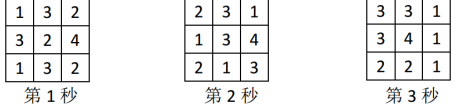
如果小空选择在第 1 行第 1 列开始游戏,那么在第 1 秒开始时她会获得 1 枚金币。接下
来,如果她选择向右走,那么在第 2 秒开始时她会出现在第 1 行第 2 列并获得 3 枚金币。接
下来, 过她选择向下进行 1 次闪现,那么在第 3 秒开始时她会出现在第 3 行第 2 列并获得 2
枚金币,游戏结束, 一共获得 6 枚金币。
又如, 在如下 5*5 的场地中(只列出了第 1 行所含金币数), 游戏共进行 2 秒, 如果小
空选择在第 1 行第 1 列开始游戏, 则她会获得 1 枚硬币,之后若向右连续闪现 2 次,那么在
第 2 秒开始时她会出现在第 1 行第 5 列, 并获得 2 枚硬币,总共获得 3 枚硬币。

现在,给出游戏场地的大小 n,每秒钟开始时各个位置会出现的金币数,小空一秒内最
多使用闪现的次数 C, 小空在整局游戏中使用闪现的最多次数 W,整局游戏的总时间 T,请
你告诉小空她最多可以获得多少枚金币。
【输入】
输入的第 1 行包含 4 个整数 n, C, W, T,意义如问题描述中所述。
接下来包含 n 个 n*n 的矩阵,第 k 个矩阵的第 i 行第 j 列表示第 i 行第 j 列的格子在第 k
秒开始时出现的金币数(记作si,j,k)。 相邻两个矩阵间用一个空行隔开。
【输出】
输出包含一个整数,表示游戏结束时小空最多可以获得的金币数量。
【输入输出样例 1】
| coin.in | coin.out |
| 3 1 1 3 1 3 4 3 2 1 1 3 2 2 3 1 1 3 2 2 1 4 3 3 1 3 2 1 2 3 1 |
11 |
见选手目录下的 coin / coin1.in 与 coin / coin1.out
【输入输出样例 1 说明】
选择在第 1 行第 3 列开始游戏, 获得 4 枚金币;在第 2 秒开始时向下闪现到第 3 行第 3
列, 获得 4 枚金币;在第 3 秒开始时向左走到第 3 行第 2 列,获得 3 枚金币, 游戏结束。一
共获得 11 枚金币。
【输入输出样例 2】
见选手目录下的 coin / coin2.in 与 coin / coin2.out
【数据规模与约定】
| 测试点编号 | n | C | W | T | si,j,k |
| 1 | ≤5 | ≤2 | ≤4 | ≤5 | ≤1,000 |
| 2 | |||||
| 3 | |||||
| 4 | ≤21 | ≤10 | ≤80 | ≤80 | |
| 5 | |||||
| 6 | |||||
| 7 | ≤25 | =100 | ≤150 | ≤100 | |
| 8 | |||||
| 9 | ≤12 | ||||
| 10 |
对 100%的数据, n≥1, C≥0, W≥0, T≥1, si,j,k≥0
分析:直接爆搜可以通过30%的数据.其实这道题阶段性特别明显,一眼就能看出是一道dp题,设f[t][k][i][j]表示在第t秒,用了k次闪现,当前位置在(i,j)的答案.转移也非常容易,从上一秒可能的位置上转移就可以了.这样dp只能通过60%的数据,因为状态数很多,每次找闪现的位置会花费大量的时间,必须对闪现的转移进行优化.
在闪现的众多状态中,只需要找到最大的那个就可以了,因为每一轮的C是固定的,可以考虑用单调队列来维护.假设从左往右闪现,闪现一次,f[t][k][i][j]从f[t-1][k-1][i-2][j]转移而来,闪现两次就从f[t-1][k-2][i-4][j]转移而来,t-1,j是固定的,只需要用单调队列维护C个f[t-1][k-p][i-2*p][j]就可以了.
30分暴力:
#include <map> #include <cmath> #include <queue> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int maxn = 25; const int dx[] = { 1, -1, 0, 0 }, dy[] = { 0, 0, 1, -1 }; int n, ans, C, W, T, a[100][maxn][maxn]; int vis[100][90][maxn][maxn]; struct node { int x, y, sum, dist, use; }; bool check(int x, int y) { if (x >= 1 && x <= n && y >= 1 && y <= n) return true; return false; } void bfs() { queue <node> q; for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) { node temp; temp.x = i; temp.y = j; temp.sum = a[1][i][j]; temp.dist = 1; temp.use = 0; q.push(temp); } while (!q.empty()) { node u = q.front(); q.pop(); int x = u.x, y = u.y, dist = u.dist, use = u.use, sum = u.sum; if (dist == T) { ans = max(ans, sum); continue; } //不闪现 for (int i = 0; i < 4; i++) { int nx = x + dx[i], ny = y + dy[i]; if (check(nx, ny)) { node v; v.dist = dist + 1; v.use = use; v.sum = sum + a[dist + 1][nx][ny]; v.x = nx; v.y = ny; q.push(v); } } //闪现 for (int i = 1; use + i <= W && i <= C; i++) { for (int j = 0; j < 4; j++) { int nx = x + i * 2 * dx[j], ny = y + i * 2 * dy[j]; if (check(nx, ny)) { node v; v.dist = dist + 1; v.use = use + i; v.sum = sum + a[dist + 1][nx][ny]; v.x = nx; v.y = ny; q.push(v); } } } node v; v.x = x; v.y = y; v.dist = dist + 1; v.use = use; v.sum = sum + a[dist + 1][x][y]; q.push(v); } } int main() { scanf("%d%d%d%d", &n, &C, &W, &T); for (int k = 1; k <= T; k++) for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) scanf("%d", &a[k][i][j]); bfs(); printf("%d ", ans); return 0; }
60分裸dp:
#include <map> #include <cmath> #include <queue> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int maxn = 25; const int dx[] = { 1, -1, 0, 0 }, dy[] = { 0, 0, 1, -1 }; int n, ans, C, W, T, a[100][maxn][maxn]; int f[100][90][maxn][maxn]; bool check(int x, int y) { if (x >= 1 && x <= n && y >= 1 && y <= n) return true; return false; } int main() { scanf("%d%d%d%d", &n, &C, &W, &T); for (int k = 1; k <= T; k++) for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) scanf("%d", &a[k][i][j]); for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) f[1][0][i][j] = a[1][i][j]; for (int t = 2; t <= T; t++) { for (int i = 1; i <= n; i++) { for (int j = 1; j <= n; j++) { for (int k = 0; k <= W; k++) { for (int p = 0; p < 4; p++) { int nx = i + dx[p], ny = j + dy[p]; if (check(nx, ny)) { f[t][k][i][j] = max(f[t][k][i][j], f[t - 1][k][nx][ny]); } for (int l = k - 1; k - l <= C; l--) { int nx = i + 2 * (k - l) * dx[p],ny = j + 2 * (k - l) * dy[p]; if (check(nx, ny)) { f[t][k][i][j] = max(f[t][k][i][j], f[t - 1][l][nx][ny]); } } } f[t][k][i][j] = max(f[t][k][i][j], f[t - 1][k][i][j]); f[t][k][i][j] += a[t][i][j]; } } } } for (int i = 1; i <= T; i++) for (int j = 0; j <= W; j++) for (int k = 1; k <= n; k++) for (int l = 1; l <= n; l++) ans = max(ans, f[i][j][k][l]); printf("%d ", ans); return 0; }
AC:
#include <queue> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int inf = 0x7fffffff; int n, C, W, T, now, last, tag, head, q[21000], cnt, tail, cur[21000], ans; int a[110][30][30], f[2][160][110][110], vis[160][160]; void init() { head = 1, tail = 0; q[1] = -inf; cnt = 0; } void push(int x) { int sum = 1; while (head <= tail && x >= q[tail]) sum += cur[tail--]; q[++tail] = x; cur[tail] = sum; if (++cnt > C) //因为有的被弹出来过,可能没有闪现C次 if (--cur[head] == 0) head++; } int main() { scanf("%d%d%d%d", &n, &C, &W, &T); for (int t = 1; t <= T; t++) for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) scanf("%d", &a[t][i][j]); for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) f[0][0][i][j] = a[1][i][j]; last = 0; now = 1; for (int t = 2; t <= T; t++) { for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) for (int k = 0; k <= W; k++) f[now][k][i][j] = -inf; for (int i = 1; i <= n; i++) { ++tag; for (int j = 1; j <= n; j++) for (int k = 0; k <= W; k++) if (vis[j][k] != tag) { init(); int nj = j, nk = k; while (nj <= n && nk <= W) { vis[nj][nk] = tag; f[now][nk][i][nj] = max(f[now][nk][i][nj], q[head]); push(f[last][nk][i][nj]); nj += 2; nk++; } } ++tag; for (int j = n; j >= 1; j--) for (int k = 0; k <= W; k++) if (vis[j][k] != tag) { init(); int nj = j, nk = k; while (nj >= 1 && nk <= W) { vis[nj][nk] = tag; f[now][nk][i][nj] = max(f[now][nk][i][nj], q[head]); push(f[last][nk][i][nj]); nj -= 2; nk++; } } } for (int j = 1; j <= n; j++) { ++tag; for (int i = 1; i <= n; i++) for (int k = 0; k <= W; k++) if (vis[i][k] != tag) { init(); int ni = i, nk = k; while (ni <= n && nk <= W) { vis[ni][nk] = tag; f[now][nk][ni][j] = max(f[now][nk][ni][j], q[head]); push(f[last][nk][ni][j]); ni += 2; nk++; } } ++tag; for (int i = n; i >= 1; i--) for (int k = 0; k <= W; k++) if (vis[i][k] != tag) { init(); int ni = i, nk = k; while (ni >= 1 && nk <= W) { vis[ni][nk] = tag; f[now][nk][ni][j] = max(f[now][nk][ni][j], q[head]); push(f[last][nk][ni][j]); ni -= 2; nk++; } } } for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) for (int k = 0; k <= W; k++) { f[now][k][i][j] = max(f[now][k][i][j], f[last][k][i - 1][j]); f[now][k][i][j] = max(f[now][k][i][j], f[last][k][i + 1][j]); f[now][k][i][j] = max(f[now][k][i][j], f[last][k][i][j - 1]); f[now][k][i][j] = max(f[now][k][i][j], f[last][k][i][j + 1]); f[now][k][i][j] = max(f[now][k][i][j], f[last][k][i][j]); f[now][k][i][j] += a[t][i][j]; } swap(now, last); } for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) for (int k = 0; k <= W; k++) ans = max(ans, f[last][k][i][j]); printf("%d ", ans); return 0; }