noip模拟赛 小Y的问题

【问题描述】
有个孩子叫小 Y，一天，小 Y 拿到了一个包含 n 个点和 n-1 条边的无向连通图， 图中的
点用 1~n 的整数编号。小 Y 突发奇想，想要数出图中有多少个“Y 字形”。
一个“Y 字形”由 5 个不同的顶点 A、 B、 C、 D、 E 以及它们之间的 4 条边组成，其中 AB、
BC、 BD、 DE 之间有边相连， 如下图所示。

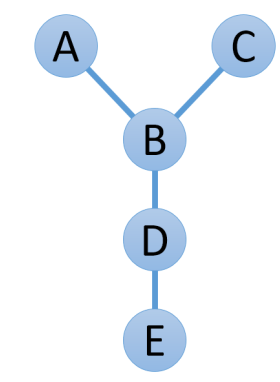
同时，无向图中的每条边都是有一定长度的。一个“Y 字形”的长度定义为构成它的四条
边的长度和。小 Y 也想知道，图中长度最大的“Y 字形”长度是多少。
【输入】
第一行包含一个整数 n，表示无向图的点数。
接下来 n 行， 每行有 3 个整数 x、 y、 z， 表示编号为 x 和 y 的点之间有一条长度为 z 的
边。
【输出】
输出包含 2 行。
第 1 行包含一个整数，表示图中的“Y 字形”的数量。
第 2 行包含一个整数，表示图中长度最大的“Y 字形”的长度。
【输入输出样例 1】

question.in	question.out
7 1 3 2 2 3 1 3 5 1 5 4 2 4 6 3 5 7 3	5 9

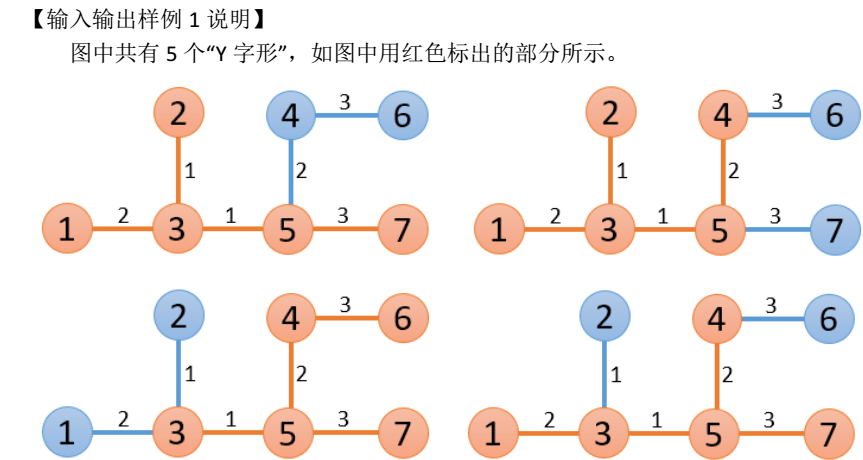
其中，长度最大的“Y 字形”是编号 3、 5、 7、 4、 6 的顶点构成的那一个，长度为 9。

【数据规模与约定】
对于 30%的数据， n≤10
对于 60%的数据， n≤2,000
对于 100%的数据， n≤200,000， 1≤x,y≤n， 1≤z≤10,000

分析：这道题很好啊.一开始我的思路错了，以为这是树形dp,推着推着发现情况太多，推不出来.

      尝试打暴力，先考虑n<=10的点，枚举Y字形的5个点或者4条边都可以，不过最好还是枚举4条边，毕竟复杂度小一些.

      60%的数据就只能枚举2个东西了，肯定是要枚举边的，枚举哪两条边呢？看哪条边最特殊、信息最多.枚举度数为3的点u和度数2的点v的中心边.然后扫一下与u相连除了v以外有多少个点x，前3大的边，对v进行同样的操作.方案数就是C(x,2) * y.对最大值的处理只需要讨论一下u,v那条边是第几大的，把另外的前3大的边加上就好了.

     60%的算法瓶颈是每次枚举一条中心边后都要花O(n)的时间来找点和边，如果能把O(n)变小，变成O(logn)甚至是O(1)就好了.很显然，预处理一下就好了，整体复杂度降为了O(n),可以通过所有数据.

     枚举题首先要看数据范围，可以知道大概要枚举多少层,枚举的对象最好选择信息最多的，如果重复枚举比较多，可以先预处理一下.

#include <map>
#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

struct node
{
    ll u, v, w;
}e[200010];

ll n, du[200010], max1[200010], max2[200010], max3[200010], ans;
ll sum;
void solve(ll x, ll y)
{
    if (y > max1[x])
    {
        max3[x] = max2[x];
        max2[x] = max1[x];
        max1[x] = y;
    }
    else
        if (y > max2[x])
        {
            max3[x] = max2[x];
            max2[x] = y;
        }
        else
            if (y > max3[x])
                max3[x] = y;
}

int main()
{
    scanf("%lld", &n);
    for (int i = 1; i < n; i++)
    {
        scanf("%lld%lld%lld", &e[i].u, &e[i].v, &e[i].w);
        du[e[i].u]++;
        du[e[i].v]++;
        solve(e[i].u, e[i].w);
        solve(e[i].v, e[i].w);
    }
    for (int i = 1; i < n; i++)
    {
        ll u = e[i].u, v = e[i].v, w = e[i].w;
        ll maxx = max(du[u], du[v]), minn = min(du[u], du[v]);
        if (!(maxx >= 3 && minn >= 2))
            continue;
        if (du[u] > 2)
        {
            long long temp = (du[u] - 1) * (du[u] - 2) / 2;
            temp *= (du[v] - 1);
            sum += temp;
            ll temp2, temp3;
            temp2 = max1[u] + max2[u];
            temp3 = max1[v];
            if (w == max1[u])
                temp2 = max2[u] + max3[u];
            if (w == max2[u])
                temp2 = max1[u] + max3[u];
            if (w == max3[u])
                temp2 = max1[u] + max2[u];
            if (w == max1[v])
                temp3 = max2[v];
            else
                temp3 = max1[v];
            ans = max(ans, temp2 + temp3 + w);
        }
        swap(u, v);
        if (du[u] > 2)
        {
            long long temp = (du[u] - 1) * (du[u] - 2) / 2;
            temp *= (du[v] - 1);
            sum += temp;
            ll temp2, temp3;
            temp2 = max1[u] + max2[u];
            temp3 = max1[v];
            if (w == max1[u])
                temp2 = max2[u] + max3[u];
            if (w == max2[u])
                temp2 = max1[u] + max3[u];
            if (w == max3[u])
                temp2 = max1[u] + max2[u];
            if (w == max1[v])
                temp3 = max2[v];
            else
                temp3 = max1[v];
            ans = max(ans, temp2 + temp3 + w);
        }
    }
    printf("%lld
%lld
", sum, ans);

    return 0;
}