【问题背景】
zhx 帮他妹子做数学题。
【问题描述】
求:
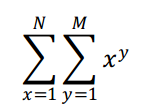
如 N=3, M=3, 这个值为 1^1+1^2+1^3+2^1+2^2+2^3+3^1+3^2+3^3=56。
【输入格式】
仅一行, 包含两个数 N 和 M.
【输出格式】
仅一行, 包含所求的答案 mod 10^9 + 7 的值。
【样例输入】
3 3
【样例输出】
56
【数据范围与规定】
对于50%的数据, 所有
对于100%的数据, 所有 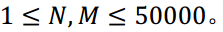
分析:50分暴力就是枚举+快速幂喽,100分的话肯定不能两层循环的枚举,固定i,看j的变化,就会发现这其实就是一个等比数列,对每个i进行一次等比数列求和就可以了.
#include <queue> #include <cstdio> #include <cstring> #include <iostream> #include <algorithm> using namespace std; const int mod = 1e9 + 7; typedef long long ll; int n, m; ll ans; ll qpow(ll a, ll b) { ll res = 1; while (b) { if (b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1; } return res; } int main() { scanf("%d%d", &n, &m); for (int i = 1; i <= n; i++) { if (i == 1) ans = (ans + m) % mod; else { ll temp = qpow(i, m) - 1; ll temp2 = temp * qpow(i - 1, mod - 2) % mod; ans = (ans + i * temp2 % mod) % mod; } } printf("%lld ", ans); return 0; }