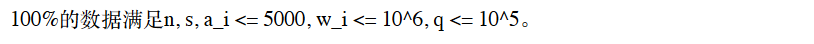Last mile of the way [树形dp+重链剖分]

$Last mile of the way$

---

$color{blue}{最初想法}$

没看见 $s le 5000$, 以为是 $s le 5000^2$, 开不下 $dp$ 数组, 事后发现自己zz了 .

---

$color{red}{正解部分}$

设 $F[i, j]$ 表示以 $i$ 为根的子树中, 选择 总大小为 $j$ 的节点所能获得的最大值,
状态转移 $F[i, j] = max( F[i, j-k] + F[to, k] )$, 时间复杂度 $O(N^3)$ .

观察到在刚开始状态转移的时候 $F[i, j]$ 是没有初值的,
于是可以在 $DFS$ 到 $i$ 点时直接继承 重儿子 信息, 其余 轻儿子 每个点都使用 $01$背包 $O(N)$ 更新 $F[i, j]$,
因为除去重儿子后 轻儿子 的规模为 $O(NlogN)$, 所以总时间复杂度 $O(N^2logN)$ .

---

$color{red}{实现部分}$

• 注意在继承重儿子的 $F$ 数组时, 当前点 $k$ 还没有被考虑在状态中, 需要使用当前点 $k$ 去更新所有能够更新的状态 .

#include<bits/stdc++.h>
#define reg register
typedef long long ll;

int read(){
        char c;
        int s = 0, flag = 1;
        while((c=getchar()) && !isdigit(c))
                if(c == '-'){ flag = -1, c = getchar(); break ;  }
        while(isdigit(c)) s = s*10 + c-'0', c = getchar();
        return s * flag;
}

const int maxn = 5005;

int N;
int num0;
int a[maxn];
int w[maxn];
int son[maxn];
int size[maxn];
int head[maxn];
int size_a[maxn];

ll F[maxn][maxn];

struct Edge{ int nxt, to; } edge[maxn << 1];

void Add(int from, int to){
        edge[++ num0] = (Edge){ head[from], to };
        head[from] = num0;
}

void DFS_1(int k, int fa){
        size[k] = 1;
        for(reg int i = head[k]; i; i = edge[i].nxt){
                int to = edge[i].to;
                if(to == fa) continue ;
                DFS_1(to, k), size[k] += size[to];
                if(size[son[k]] < size[to]) son[k] = to;
        }
}

void DFS_3(ll *f, int k, int fa){
        for(reg int i = 5000; i >= a[k]; i --) f[i] = std::max(f[i], f[i-a[k]]+w[k]);
        for(reg int i = head[k]; i; i = edge[i].nxt) if(edge[i].to != fa) DFS_3(f, edge[i].to, k);
}

void DFS_2(int k, int fa){
        size_a[k] = a[k];
        if(son[k]) DFS_2(son[k], k), size_a[k] += size_a[son[k]];
        memcpy(F[k], F[son[k]], sizeof F[k]);
        for(reg int i = 5000; i >= a[k]; i --) F[k][i] = std::max(F[k][i], F[k][i-a[k]]+w[k]);
        for(reg int i = head[k]; i; i = edge[i].nxt){
                int to = edge[i].to;
                if(to == son[k] || to == fa) continue ;
                DFS_2(to, k);
                size_a[k] += size_a[to];
                DFS_3(F[k], to, k);
/*              暴力更新
                for(reg int j = std::min(5000, size_a[k]); j >= 1; j --)
                        for(reg int p = 1; p <= std::min(j, size_a[to]); p ++)
                                F[k][j] = std::max(F[k][j], F[k][j-p] + F[to][p]);
*/
        }
}

int main(){
        N = read();
        for(reg int i = 1; i < N; i ++){
                int u = read(), v = read();
                Add(u, v), Add(v, u);
        }
        for(reg int i = 1; i <= N; i ++) w[i] = read(), a[i] = read();
        DFS_1(1, 0), DFS_2(1, 0);
        for(reg int i = 1; i <= N; i ++)
                for(reg int j = 1; j <= 5000; j ++) F[i][j] = std::max(F[i][j], F[i][j-1]);
        /*
        for(reg int i = 1; i <= N; i ++){
                printf("==========%d===========
", i);
                for(reg int j = 1; j <= size_a[i]; j ++)
                        printf("%d: %lld
", j, F[i][j]);
        }
        */
        int Q_ = read();
        for(reg int i = 1; i <= Q_; i ++){
                int pos = read(), x = read();
                printf("%lld
", F[pos][x]);
        }
        return 0;
}