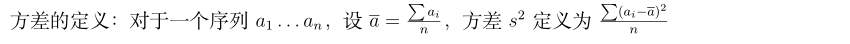序列方差 [线段树, 推式子, 组合数, NTT]

$序列方差$

---

$color{red}{正解部分}$

考虑一个长度为 $m$ 的 子序列 对答案的贡献,

$egin{aligned} & frac{1}{m}sum_{i=1}^m (a_i - overline{a})^2 \ & = frac{1}{m} left( sum_{i=1}^m a_i^2 + sum_{i=1}^m overline{a}^2 - 2 sum_{i=1}^ma_ioverline{a} ight)\ & = frac{1}{m} left( sum_{i=1}^ma_i^2 + m frac{left(sum_{i=1}^m a_i ight)^2}{m^2} - 2 sum_{i=1}^m a_i frac{sum_{j=1}^m a_j}{m} ight)\ & = frac{1}{m} left( sum_{i=1}^ma_i^2 + frac{1}{m}left(sum_{i=1}^ma_i ight)^2 -frac{2}{m}left(sum_{i=1}^ma_i ight)^2 ight)\ & = frac{1}{m} left( sum_{i=1}^ma_i^2 - frac{1}{m}left(sum_{i=1}^ma_i ight)^2 ight) \ & = frac{1}{m} sum_{i=1}^ma_i^2 - frac{1}{m^2}left(sum_{i=1}^ma_i ight)^2 end{aligned}$

---

但是现在要计算一个序列中的 所有子序列 的 贡献和, 假设当前询问区间是 $[1, n]$,

对一个数字 $a_i$ 单独考虑其对答案的贡献, $frac{1}{m} sumlimits_{i=1}^ma_i^2 - frac{1}{m^2}left(sumlimits_{i=1}^ma_i ight)^2$,

先计算这个式子左项, 为 $frac{1}{m} egin{pmatrix} n-1 \ m-1 end{pmatrix} sumlimits_{i=1}^n a_i^2$,

再考虑这个式子右项, 为 $-frac{1}{m^2} left{ egin{pmatrix} n-1 \ m-1 end{pmatrix} sumlimits_{i=1}^n a_i^2 + egin{pmatrix} n-2 \ m-2 end{pmatrix} sumlimits_{i=1}^n a_ileft[ (sumlimits_{j=1}^n a_j) - a_i ight] ight}$
继续化简得到 $-frac{1}{m^2} left{ egin{pmatrix} n-1 \ m-1 end{pmatrix} sumlimits_{i=1}^n a_i^2 + egin{pmatrix} n-2 \ m-2 end{pmatrix} left[left(sumlimits_{i=1}^n a_i ight)^2 - sumlimits_{i=1}^na_i^2 ight] ight}$ .

设 $f(n) = sum_{i=1}^n a_i^2, g(n) = sum_{i=1}^n a_i$, 合并两项, 得到 总贡献,

$left(frac{1}{m}- frac{1}{m^2} ight)egin{pmatrix} n-1 \ m-1end{pmatrix} f(n) - frac{1}{m^2} egin{pmatrix} n-2 \ m-2 end{pmatrix}left[g(n)^2 - f(n) ight]$

将 组合数 展开, 可得

$frac{(n-1)!}{m^2(n-m)!(m-2)!}f(n) - frac{(n-2)!}{m^2(n-m)!(m-2)!}[g(n)^2 - f(n)]$ .

分母是一样的, 设两个多项式 $p_1(x) = x! p_2(x) = x^2(x-2)!$, 则两个多项式的 卷积 的 $n$ 次项系数即为 分母 的总和 .

再配合 线段树 计算 $f(n), g(n)^2$ 即可 $O(nlog n)$ 解决这道题 .

---

$color{red}{实现部分}$

#include<bits/stdc++.h>
#define reg register

const int maxn = 1e6 + 5;
const int mod = 998244353;

int read(){
        char c;
        int s = 0, flag = 1;
        while((c=getchar()) && !isdigit(c))
                if(c == '-'){ flag = -1, c = getchar(); break ; }
        while(isdigit(c)) s = s*10 + c-'0', c = getchar();
        return s * flag;
}

int N;
int Q_;
int Tmp_1;
int ntt_len;
int p1[maxn];
int p2[maxn];
int fac[maxn];
int rev[maxn];

int Ksm(int a, int b){ int s=1; while(b){ if(b&1) s=1ll*s*a%mod; a=1ll*a*a%mod; b>>=1; } return s; }

void Ntt(int *f, int opt){
        for(reg int i = 0; i < ntt_len; i ++) if(i < rev[i]) std::swap(f[i], f[rev[i]]);
        for(reg int p = 2; p <= ntt_len; p <<= 1){
                int half = p >> 1;
                int wn = Ksm(3, (mod-1)/p);
                if(opt == -1) wn = Ksm(wn, mod-2);
                for(reg int i = 0; i < ntt_len; i += p){
                        int t = 1;
                        for(reg int j = i; j < i+half; j ++){
                                int tmp = 1ll*t*f[j+half] % mod;
                                f[j+half] = (f[j] - tmp + mod) % mod; f[j] = (f[j] + tmp) % mod;
                                t = 1ll*t*wn % mod;
                        }
                }
        }
}

struct Segment_Tree{

        struct Node{ int l, r, s1, s2, tag; } T[maxn << 3];

        void Build(int k, int l, int r){
                T[k].l = l, T[k].r = r;
                if(l == r) return ;
                int mid = l+r >> 1;
                Build(k<<1, l, mid), Build(k<<1|1, mid+1, r);
        }

        void Push_down(int k){
                int l = T[k].l, r = T[k].r;
                T[k].s2 = (T[k].s2 + (2ll*T[k].s1*T[k].tag%mod + (1ll*r-l+1)*T[k].tag%mod*T[k].tag%mod)%mod)%mod; 
                T[k].s1 = (T[k].s1 + 1ll*(r-l+1)*T[k].tag%mod) % mod;
                T[k<<1].tag = (T[k<<1].tag + T[k].tag) % mod, T[k<<1|1].tag = (T[k<<1|1].tag + T[k].tag) % mod;
                T[k].tag = 0;
        }

        void Modify(int k, const int &ql, const int &qr, const int &aim){
                int l = T[k].l, r = T[k].r;
                if(T[k].tag) Push_down(k);
                if(r < ql || l > qr) return ;
                if(ql <= l && r <= qr){ T[k].tag = (T[k].tag + aim) % mod; Push_down(k); return ; }
                int mid = l+r >> 1;
                Modify(k<<1, ql, qr, aim), Modify(k<<1|1, ql, qr, aim);
                T[k].s1 = (T[k<<1].s1 + T[k<<1|1].s1) % mod, T[k].s2 = (T[k<<1].s2 + T[k<<1|1].s2) % mod;
        }

        int Query(int k, const int &ql, const int &qr, const int &opt){
                int l = T[k].l, r = T[k].r;
                if(T[k].tag) Push_down(k);
                if(ql <= l && r <= qr) return opt?T[k].s1:T[k].s2;
                int mid = l+r >> 1, s = 0;
                if(ql <= mid) s = (s + Query(k<<1, ql, qr, opt)) % mod;
                if(qr > mid) s = (s + Query(k<<1|1, ql, qr, opt)) % mod;
                return s;
        }

} seg_t;

int main(){
        N = read(), Q_ = read(), read();
        fac[0] = 1; for(reg int i = 1; i <= N; i ++) fac[i] = 1ll*fac[i-1]*i % mod;
        for(reg int i = 0; i <= N; i ++) p1[i] = Ksm(fac[i], mod-2);
        for(reg int i = 2; i <= N; i ++) p2[i] = Ksm(1ll*i*i%mod*fac[i-2]%mod, mod-2);
        ntt_len = 1; int bit_cnt = 0;
        while(ntt_len <= (N << 1)) ntt_len <<= 1, bit_cnt ++;
        for(reg int i = 0; i < ntt_len; i ++) rev[i] = (rev[i>>1]>>1) | ((i&1)<<bit_cnt-1);
        Ntt(p1, 1), Ntt(p2, 1);
        for(reg int i = 0; i < ntt_len; i ++) p1[i] = 1ll*p1[i]*p2[i] % mod;
        Ntt(p1, -1); int INV = Ksm(ntt_len, mod-2);
        for(reg int i = 0; i < ntt_len; i ++) p1[i] = 1ll*INV*p1[i] % mod;
        seg_t.Build(1, 1, N);
        for(reg int i = 1; i <= N; i ++) seg_t.Modify(1, i, i, read());
        while(Q_ --){
                int opt = read(), l = read(), r = read();
                if(opt == 1) seg_t.Modify(1, l, r, read()); 
                else{
                        int n = r-l+1, f = seg_t.Query(1, l, r, 0), g = seg_t.Query(1, l, r, 1);
                        g = (1ll*g*g%mod - f + mod) % mod;
                        int Ans = 1ll*p1[n]*fac[n-1]%mod*f%mod;
                        Ans -= 1ll*p1[n]*fac[n-2]%mod*g%mod; Ans += mod, Ans %= mod;
                        printf("%d
", Ans);
                }
        } 
        return 0;
}