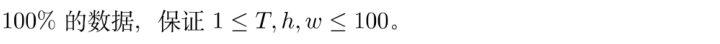硬币游戏 [博弈论, 思维题]

$硬币游戏$

---

$color{red}{正解部分}$

首先对于无解的情况, 直接判断 $h+w$ 是否奇数, 若是奇数, 则先手必胜, 反之先手必败 .

接下来判断是否有解, 每行 和 每列 都有 状态 $0/1$, 分别表示操作与不操作,

对于每个棋子 $(x, y)$,

• 若其是 正面朝上, $x_0$ 与 $y_0$ 之间连边, $x_1$ 与 $y_1$ 之间连边 .
• 若其是 反面朝上, $x_0$ 与 $y_1$ 之间连边, $x_1$ 与 $y_0$ 之间连边 .

最后会得到 若干联通块, 显然每个 联通块 都有与其对应的 “反联通块”, 两个 联通块 内的边都是受相同棋子影响而链成的 .

先判断是否有 联通块 内部同时含有类似 $x_0, x_1$ 或者 $y_0, y_1$ 的冲突情况, 若有, 必定 无解,
否则有解, 按照 “双方都会执行最优策略以使得自己得分最高” 的题目条件, 所有硬币必定会翻为正面,

于是现在的问题就是谁会取得最后一步,

计算出每个 联通块 内部的 $c_0, c_1$ 分别表示 状态 $0$ 和 状态 $1$ 的个数 的 奇偶性,
然后将 联通块 分类, 分为 $(1, 0)/(0,1)$, $(1, 1)$, $(0, 0)$ 三类, 在下面分别称为 $A,B,C$ 类 联通块, 个数 奇偶性 分别为 $x, y, z$ .

$C$ 类联通块的操作次数始终为偶数, 不会对先手造成影响, 应忽略不计,

于是影响答案的仅有 $x$ 和 $y$ 的取值了, 接下来进行 分类讨论,

• $x = 1, y = 1$, 先手选择 $(0, 1)$ 使得总操作数为 奇, 先手胜 .
• $x = 0, y = 1$, 总操作数 奇数, 先手胜 .
• $x = 1, y = 0$, 先手选择 $(0, 1)$ 使得总操作数为 奇, 先手胜 .
• $x = 0, y = 0$, 总操作数仅能为 偶, 先手败 .

$herefore$ 若 $x || y$, 则 先手必胜 .

---

$color{red}{实现部分}$

实现时, 关于行 $x$ 的状态, 使用 $2x$ 和 $2x+1$ 表示, 关于列 $y$ 的状态, 使用 $2(y + H)$ 和 $2(y + H) + 1$ 表示 .

然后使用并查集维护联通块即可 .

#include<bits/stdc++.h>
#define reg register

const int maxn = 1005;

int read(){
        char c;
        int s = 0, flag = 1;
        while((c=getchar()) && !isdigit(c))
                if(c == '-'){ flag = -1, c = getchar(); break ; }
        while(isdigit(c)) s = s*10 + c-'0', c = getchar();
        return s * flag;
}

int H;
int W;
int Tot;
int F[maxn];
int c0[maxn];
int c1[maxn];

char C[maxn][maxn];

int Find(int x){ return F[x]==x?x:F[x]=Find(F[x]); }

void Work(){
        H = read(), W = read(), Tot = H+W<<1|1;
        for(reg int i = 1; i <= H; i ++) scanf("%s", C[i]+1);
        for(reg int i = 1; i <= Tot; i ++) F[i] = i, c0[i] = c1[i] = 0;
        for(reg int i = 1; i <= H; i ++)
                for(reg int j = 1; j <= W; j ++)
                        if(C[i][j] == 'e') continue ;
                        else{
                                int x1 = i<<1, x0 = i<<1|1;
                                int y1 = (H+j)<<1, y0 = (H+j)<<1|1;
                                if(C[i][j] == 'x') F[Find(x1)] = Find(y0), F[Find(x0)] = Find(y1);
                                else F[Find(x1)] = Find(y1), F[Find(x0)] = Find(y0);
                        }
        for(reg int i = 1; i <= H+W; i ++)
                if(Find(i<<1) == Find(i<<1|1)){ printf("%d
", (H+W) & 1); return ; }
        for(reg int i = 2; i <= Tot; i ++){
                int anc = Find(i);
                if(i & 1) c0[anc] ^= 1; else c1[anc] ^= 1;
        }
        int x = 0, y = 0;
        for(reg int i = 2; i <= Tot; i ++){
                if(i != Find(i)) continue ;
                if(c0[i] && c1[i]) y ++;
                else if(c0[i] || c1[i]) x ++;
        }
        x >>= 1, y >>= 1, x &= 1, y &= 1;
        if(x || y) printf("3
");
        else printf("2
");
}

int main(){
        int T = read();
        while(T --) Work();
        return 0;
}