优雅,永不过时。
暴力的艺术,艺术的暴力——分块。
Part 1 分块原理
众所周知,线段树和树状数组都可以在 (log(n)) 的时间里解决序列区间求和的问题。但是使用线段树或者树状数组有一个前提:必须满足区间可加性原则。有一些不满足区间可加原则的值(譬如众数),很难使用线段树或者树状数组进行维护。并且有时候,线段树和树状数组的代码并不直观,导致在调试的时候比较艰难……
那么有没有一种扩展性强,简单易懂,可以维护区间信息的数据结构呢?
答案是:分块。
与线段树和树状数组相比,分块没有选择把区间层层分段到只有一个元素,而是分成若干个小段(常用的小段长是 (sqrt n) ),对每一个小段进行整体维护。至于不足段或者单个元素的修改……emmmm暴力它不香吗?
比如这样,对于一个数组 A :
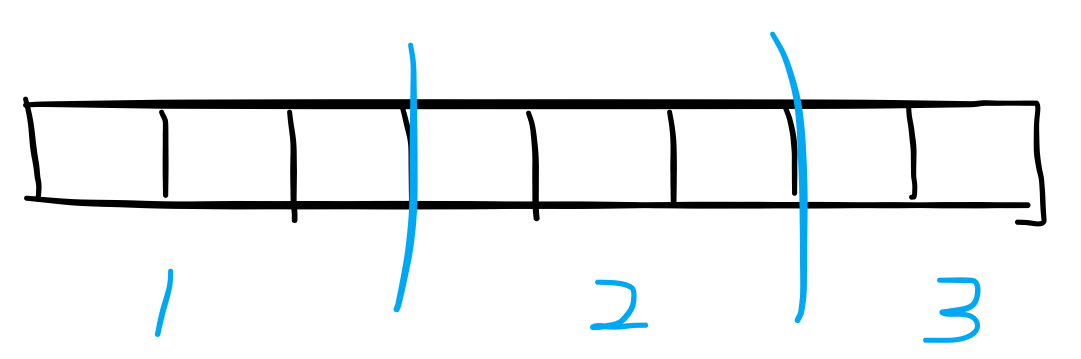
我们可以把 A 分成 3 段(蓝色线隔开)。
利用 sum[i] 记录第 i 段的区间和,add[i] 表示第 i 段的增量标记(具体作用之后会说),sum 数组需要提前预处理,add 数组初始为 0 。
假设要把 A[2] ~ A[7] 这 7 个元素加上 d 。
这个修改包含了 2 段的所有元素,利用增量数组 add 进行整段维护,直接更新整段的 sum 值。add[2]+=d;sum[2]+=len*d;( len 是段长,这里为 3 )。
2 3 7 不是整段,直接暴力的在原数组 A[i] 上加 d ,循环的时候顺便更新 sum 数组。
for(2 to 3) A[i]+=d,sum[i]+=d; for(7 to 7) A[i]+=d,sum[i]+=d;
假设要查询 A[2]~A[7] 这 7 个元素的和。
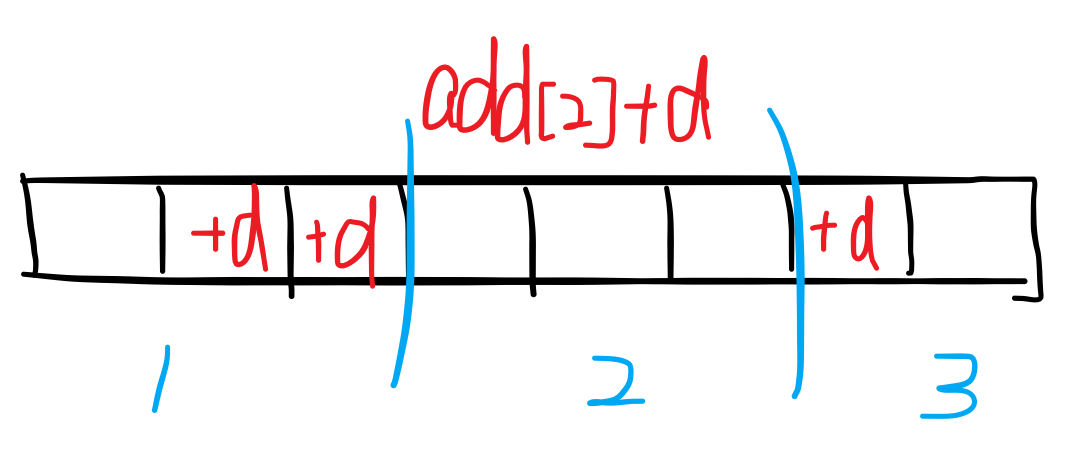
查询包含了 2 段的所有元素,那么
ans+=sum[2];
答案还包括 2 3 7,直接暴力加进去。不过这里记得,整段修改的时候,我们不对段内的单个元素更新,而是寄存在 add 数组里,所以 A 中的元素 A[i] 一般不是真实值,A[i]+add[j] ( j 表示元素 A[i] 所处的段)才是真实值。
for(2 to 3) ans+=(A[i]+add[1]); for(7 to 7)ans+=(A[i]+add[3]);
最后 ans 就是答案。
Part 2 分块优势/应用
与线段树等相比,分块的做法更接近于“暴力”,所以它的效率通常没有线段树这些精致的数据结构高。但是因为分块在维护的时候,并不需要满足区间可加、可减性原则,因而可以更为广泛的应用到序列问题中。因为分块带有暴力的性质,对于一些题目可以大大减少其思维量。另外,分块算法有时可以替代一些复杂的数据结构,比如二逼平衡树、文艺平衡树等等。
光说不练假把式,下面来用几道例题,感受一下分块的暴力美学。
例1 区间加、区间和
给定一个长度为 (n(nleq 1e5)) 的序列 (A) ,有 (T) 次操作,每次给定一个操作参数 (op) ,
1、若 (op=1) ,再给定三个整数 (i,j,m) ,使 (A_k(ileq k leq j)) 加 (m) 。
2、若 (op=2) ,再给定两个整数 (i,j) ,求 (sum^{j}_{k=i} A_k) 的值。
这个问题可以使用线段树在 (O(nlogn)) 的时间内解决,现在看看分块解法。
和前面讲的原理差不多,判断区间加属于哪几个段,维护 sum、add 数组,不足一段的暴力处理;
统计的时候,答案在整段直接加 sum ,不足整段的加 (A_i+add_j) ;(其中 (j) 是值 (A_i) 所处的段)
总时间复杂度 (O(nsqrt n)) 。
代码:
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<iostream>
#define ll long long
using namespace std;
inline ll read(){
ll x=0,fh=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')
fh=-1;
ch=getchar();
}
while(isdigit(ch)){
x=(x<<3)+(x<<1)+ch-'0';
ch=getchar();
}
return fh*x;
}
const int maxn=100005;
ll a[maxn],n,m;
ll L[maxn],R[maxn],belong[maxn],add[maxn],sum[maxn];
//L[i]/R[i]表示第i段的左端点,右端点,belong[i]表示第i个元素属于第几个块
//add表示增量标记,sum[i]表示第i段的和
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++)
a[i]=read();
int k=sqrt(n);
for(int i=1;i<= (n%k==0 ? n/k :n/k+1) ;i++){//预处理分块
L[i]=1+(i-1)*k;
R[i]=min(n,L[i]+k-1);
for(int j=L[i];j<=R[i];j++){
sum[i]+=a[j];//预处理出每一段的和
belong[j]=i;//第j个元素属于第i块
}
}
for(ll i=0,op,l,r,k,p,q;i<m;i++){
op=read();
if(op==1){
l=read(),r=read(),k=read();
if(belong[l]==belong[r]){//属于同一块,直接暴力
for(int j=l;j<=r;j++){
a[j]+=k;sum[belong[l]]+=k;//虽然暴力很快乐,但别忘更新sum
}
}else{
p=belong[l],q=belong[r];
//记下来第l个元素属于第p段,而第r个属于第q段
for(int j=p+1;j<=q-1;j++){
//那么p+1到q-1段都在这两段之间,整段更新
add[j]+=k;sum[j]+=(R[j]-L[j]+1)*k;
}
for(int j=l;j<=R[p];j++){
a[j]+=k;sum[p]+=k;//单独更新最左边一段
}
for(int j=L[q];j<=r;j++){
a[j]+=k;sum[q]+=k;//单独更新最右边一段
}
}
}else{
l=read(),r=read();
ll ans=0;
if(belong[l]==belong[r]){//类似修改,属于同一段的直接暴力查询
for(int j=l;j<=r;j++)
ans+=(a[j]+add[belong[l]]);
printf("%lld
",ans);
}else{
p=belong[l],q=belong[r];
for(int j=p+1;j<=q-1;j++)
//中间段整段累加
ans+=sum[j];
for(int j=l;j<=R[p];j++)
ans+=(a[j]+add[p]);//单独暴力累加最左段
for(int j=L[q];j<=r;j++)
ans+=(a[j]+add[q]);//单独暴力累加最右段
printf("%lld
",ans);
}
}
}
return 0;
}
例2 区间加、区间乘、区间和
给定一个长度为 (n(nleq 1e5)) 的序列 (A) ,给定一个模数 (p) ,有 (T) 次操作,每次给定一个操作参数 (op) ,
1、若 (op=1) ,再给定三个整数 (i,j,m) ,使 (A_k(ileq k leq j)) 乘 (m) 。
2、若 (op=2) ,再给定三个整数 (i,j,m) ,使 (A_k(ileq k leq j)) 加 (m) 。
3、若 (op=3) ,再给定两个整数 (i,j) ,求 (sum^{j}_{k=i} A_k) 对 (p) 取模的值。
这个题同样可以使用线段树在 (O(Tlogn)) 时间内解决,但是对于懒标记的设计相对于例1有着更高的要求,因为这里涉及到先加后乘还是先乘后加的问题。我们不妨在这里讨论一下线段树的做法,以此与分块形成对比。
解法1:线段树
涉及到两种操作:加和乘。这里很显然有 ((a+b) imes c e a imes c +b) ,什么意思呢,就是说这里涉及到顺序问题。加操作和乘操作必须要分开计算,不可以混在一起,否则顺序不对会导致答案错误。
一种解决办法就是当有乘操作的时候,直接把涉及到的节点的加标记下传到叶子节点。这样解决了顺序问题,但是如果每次都暴力下传的话,很容易导致时间复杂度退化为 (O(n)) 。
那怎么办呢?既然要分开计算,那不妨搞两个懒标记,一个用来记加 ( add ),一个用来记乘 ( mul )。
1、更新当前区间和
假设有一段区间是 (A_i) 到 (A_j) 。从最简单的情况考虑,假设当前区间的 mul 标记的值为 1 (没乘过),而现在要给这段区间的每一个元素都乘上 (b) 。
那么设现在的区间和是 (v=sum^j_{k=i} (A_k imes b)=bsum^j_{k=i} A_k) 。发现直接把原来的区间和乘 (b) 就行了。
2、下传时更新子区间和
推理一下,假设某个区间的有子区间,且其中一个元素的值是 (a) 。
现在有 4 次操作:加 (b) 、乘 (c) 、加 (d) 、乘 (e) 。
那么现在的和应该是 (left[(a+b)c+d ight]e=ace+(bc+d)e) 。
观察式子,发现 (ce) 是两次乘法操作的积,这里我们的 mul 标记记录的正好就是两次操作的积,下传时直接用 (a) 乘标记的值就完事了。看看剩下的式子,好像不太好计算?没关系,这里是数学多项式迷惑了我们的思路,我们不妨换一换思维方式,用程序设计的思维来想。
如果给你 (b,c,d,e) 四个整数,让你求 ((bc+d)e) 的值,你会怎么做?
你肯定会不假思索的写出这样的代码:
#include<iostream>
using namespace std;
int main(){
int ans=0;
int b,c,d,e;
cin>>b>>c>>d>>e;
ans+=b;ans*=c;ans+=d;ans*=e;
cout<<ans;
return 0;
}
其实我们的 add 标记就是上面的 ans ,它在记录加的同时,也要记录乘。
打加法标记?那我 add+=x;打乘法标记?那我 add*=x。
这样记录下的 add 就是上面所说的 ((bc+d)e) 的值啦!
总体来说,我们下传标记的时候,先下传乘法标记,然后下传加法标记,注意上面讲到的对加法标记的特殊处理就可以了。子区间的和就是 (v imes mul+len imes add) (其中 len 为区间长度,v 为原区间和)。
3、下传时更新子区间的两个标记
下传的时候,除了子区间和要更新,子区间的标记也要更新。
与统计区间和类似,下传的时候,也要先下传乘法标记,左右儿子的乘法标记乘上 (mul) 。注意此时乘了 (mul) 之后,加法标记也要乘上 (mul) (具体原因上面已经分析过),然后再加上父节点的 (add) 。
写出代码:
#include<cstdio>
using namespace std;
typedef long long LL;
const int maxn=100005;
int n,q,mod;
LL a[maxn];
struct Node{
LL add,mul,v;
int l,r;
Node *ls,*rs;
Node(const int L,const int R){//建树
l=L,r=R;
if(l==r){
add=0;
mul=1;
v=a[l];
ls=rs=NULL;
}else{
add=0;
mul=1;
int Mid=(L+R)/2;
ls=new Node(L,Mid);
rs=new Node(Mid+1,R);
push_up();
}
}
inline void make_add(const LL w){//打加法标记
v+=(r-l+1)*w;
add+=w;
}
inline void make_mul(const LL w){//打乘法标记
add=(add*w)%mod;//上面分析过,乘法的时候,add也乘w
mul=(mul*w)%mod;
v=(v*w)%mod;
}
inline void push_up() { v=(ls->v+rs->v)%mod; }//更新区间和
inline void push_down(){//按照上面分析过的方法,向下传递标记
ls->v=(LL)((mul*ls->v)+((ls->r-ls->l+1)*add)%mod)%mod;
rs->v=(LL)((mul*rs->v)+((rs->r-rs->l+1)*add)%mod)%mod;
//更新子区间的和
ls->mul=(LL)(ls->mul*mul)%mod;
rs->mul=(LL)(rs->mul*mul)%mod;
ls->add=(LL)(ls->add*mul+add)%mod;
rs->add=(LL)(rs->add*mul+add)%mod;
//更新子区间的标记
mul=1;add=0;//注意这里mul是1,如果是0的话那么乘法会爆0
}
inline bool In_Range(const int L,const int R) { return (L<=l)&&(r<=R); }
inline bool Outof_Range(const int L,const int R) { return (l>R)||(r<L); }
//这两个函数是判断当前区间是不是完整包含于修改区间
void up_add(const int L,const int R,const LL w){
if(In_Range(L,R)==true) make_add(w);
else if(!Outof_Range(L,R)){
push_down();
ls->up_add(L,R,w);
rs->up_add(L,R,w);
push_up();
}
}//加法操作
void up_mul(const int L,const int R,const LL w){
if(In_Range(L,R)==true) make_mul(w);
else if(!Outof_Range(L,R)){
push_down();
ls->up_mul(L,R,w);
rs->up_mul(L,R,w);
push_up();
}
}//乘法操作
LL query(const int L,const int R){
if(In_Range(L,R)==true) return v;
if(Outof_Range(L,R)==true) return 0;
push_down();
return ((ls->query(L,R))%mod+(rs->query(L,R))%mod)%mod;
}//查询操作
};
int main(){
scanf("%d%d%d",&n,&q,&mod);
for(int i=1;i<=n;i++)
scanf("%lld",a+i);
Node *rot=new Node(1,n);
for(LL o,l,r,x;q>0;q--){
scanf("%lld%lld%lld",&o,&l,&r);
if(o==1){
scanf("%lld",&x);
rot->up_mul(l,r,x);
}
if(o==2){
scanf("%lld",&x);
rot->up_add(l,r,x);
}
if(o==3) printf("%lld
",rot->query(l,r));
}
return 0;
}
解法2 分块
和线段树解法相似的,分块也需要搞两个标记数组 add 和 mul 。
加法修改的时候,和例1一样,整段打标记,零散段直接暴力。乘法修改的时候,整段打标记,同时别忘了把 add 数组也乘一下(原理同上),零散段暴力处理。
但出现了两个问题:
1、假设现在有一个零散段(假设它完全被包含于第 (k) 段) ([l,r]) 要乘上 (m) ,我们的做法是直接暴力把 (A_l) 到 (A_r) 的所有元素直接乘上 (m) 。然而实际上这样的做法并不对,这个段里的元素 (A_i) ( (lleq ileq r))的真实值是 (A_i imes mul_k+add_k) 。如果暴力,那么答案就变成了 (A_i imes mul_k imes m+add_k) ,然而真实的答案是$ m(A_i imes mul_k+add_k) $。这样一来一回,两个答案差了 (add_k(m-1)) 。按道理来说,如果想要暴力修改,得把 (add_k) 也乘 (m) 。但是 (add_k) 表示的是一整段的加法标记,不可能因为某几个元素的修改就跟着修改。
2、假设现在有一个零散段(假设它完全被包含于第 (k) 段) ([l,r]) 要加上 (m) ,我们的做法是直接暴力把 (A_l) 到 (A_r) 的所有元素直接加上 (m) 。然而实际上这样的做法并不对,这个段里的元素 (A_i) ( (lleq ileq r))的真实值是 (A_i imes mul_k+add_k) 。如果暴力,那么答案就变成了 ((A_i+m) imes mul_k +add_k) ,然而真实的答案是$ A_i imes mul_k+add_k +m$。这样一来一回,两个答案差了 (m(mul_k-1)) 。按道理来说,如果想要暴力修改,得把 加数 (m) 变成 (frac{m}{mul_k}) 。但是运算中加入除法会导致加数变成奇奇怪怪的分数小数爆精度,我们的内心是拒绝的。
怎么办?暴力啊!直接把这一整段的 (mul_k) 和 (add_k) 下传到 (A_i) 上,(A_i) 里存的就是真实值了!然后再暴力把每一个元素都乘上 (m) ,或者加上 (m) ,不就完成了修改么?
因为是零散段,每一个零散段的长度不超过 (sqrt n) ,所以对零散段的暴力下传标记的复杂度应该是 (sqrt n) ,这样的做法看似暴力,但是也是符合分块的时间复杂度的(最多算带个 4 倍常数)。这样总复杂度 (O(Tsqrt n)) 。
这里分块的做法不用考虑如何更新儿子节点的标记的问题,节约了思维量。
写出代码:
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<iostream>
using namespace std;
#define ll long long
const ll maxn=100005;
ll mod;
inline ll read(){
ll x=0,fh=1;
char ch=getchar();
while(!isdigit(ch)){
if(ch=='-')
fh=-1;
ch=getchar();
}
while(isdigit(ch)){
x=(x<<3)+(x<<1)+ch-'0';
ch=getchar();
}
return x*fh;
}
ll A[maxn],add[maxn],tme[maxn],L[maxn],R[maxn],belong[maxn],sum[maxn];
//这里乘法标记我用的是tme数组,其他同例1
ll n,m;
inline void reset(const int x){
for(int i=L[x];i<=R[x];i++)
A[i]=( A[i]*tme[x] + add[x] )%mod;
tme[x]=1,add[x]=0;
}//暴力下传标记
signed main(){
n=read(),m=read(),mod=read();
for(int i=1;i<=n;i++)
A[i]=read();
ll len=sqrt(n);
for(int i=1;i<=(n%len==0?n/len:n/len+1);i++){
L[i]=1+(i-1)*len;
R[i]=min(n,L[i]+len-1);
tme[i]=1;
for(int j=L[i];j<=R[i];j++){
sum[i]=( sum[i]%mod + A[j]%mod )%mod;
belong[j]=i;
}
}
for(ll i=0,op,l,r,k;i<m;i++){
op=read(),l=read(),r=read();
if(op==1){//乘k
k=read();
int p=belong[l],q=belong[r];
if(p==q){
reset(p);//零散段下传
for(int j=l;j<=r;j++){//零散段暴力
sum[p]=( sum[p] + A[j] * (k-1) )%mod;
A[j]=( A[j] * k ) %mod;
}
}else{
for(int j=p+1;j<=q-1;j++){//整段更新
add[j]=( add[j] * k )%mod;
tme[j]=( tme[j] * k )%mod;
sum[j]=( sum[j] * k )%mod;
}
reset(p);reset(q);//零散段下传
for(int j=l;j<=R[p];j++){//零散段暴力
sum[p]=( sum[p] + A[j] * (k-1) )%mod;
A[j]=( A[j] * k ) %mod;
}
for(int j=L[q];j<=r;j++){
sum[q]=( sum[q] + A[j] * (k-1) )%mod;
A[j]=( A[j] * k ) %mod;
}
}
}else if(op==2){
k=read();//这一堆都同上
int p=belong[l],q=belong[r];
if(p==q){
reset(p);
for(int j=l;j<=r;j++){
A[j]=( A[j] + k )%mod;
sum[p]=( sum[p] + k )%mod;
}
}else{
for(int j=p+1;j<=q-1;j++){
sum[j]=( sum[j] + (len*k) )%mod;
add[j]=( add[j] + k )%mod;
}
reset(p);reset(q);
for(int j=l;j<=R[p];j++){
A[j]=( A[j] + k )%mod;
sum[p]=( sum[p] + k )%mod;
}
for(int j=L[q];j<=r;j++){
A[j]=( A[j] + k )%mod;
sum[q]=( sum[q] + k )%mod;
}
}
}else{
ll ans=0;
int p=belong[l],q=belong[r];
if(p==q){//和线段树的查询差不多,先乘后加
for(int j=l;j<=r;j++)
ans=( ans + add[p] + A[j] * tme[p] )%mod;
printf("%lld
",ans);
}else{
for(int j=l;j<=R[p];j++)
ans=( ans + add[p] + A[j] * tme[p] )%mod;
for(int j=p+1;j<=q-1;j++)
ans=( ans + sum[j] )%mod;
for(int j=L[q];j<=r;j++)
ans=( ans + add[q] + A[j] * tme[q] )%mod;
printf("%lld
",ans);
}
}
}
return 0;
}
今天的分享先到这里,以后还会有别的分块博客,敬请期待