Treap 详解

平衡树 Treap 详解

吐槽：网上关于平衡树的详解，解答的不是很详细。并且大部分只谈原理，没有涉及到代码实现，即使给出了代码也没有添加注释，导致我找了很长时间才明白了原理并且写出一棵 Treap 。

Part 1 关于平衡树

平衡树的实质是一棵二叉搜索树（BIT），二叉搜索树是一颗有根二叉树，并且满足这样的性质：

每个节点带有一个权值，如果对这个二叉树进行中序遍历，得到的权值序列是一个单调递增的序列。

换句话说，这颗二叉树的每一个以节点 (V) 为根的子树中，其左子树 (V_l) 中每个节点的权值必然小于节点 (V) 的权值，其右子树 (V_r) 中每个节点的权值必然大于节点 (V) 的权值。

看起来很好构建满足这样性质的一棵树，对吧？我们只要在每次插入新节点的时候从根节点递归比大小，决定要往左子树插还是右子树插，最后找到满足性质的位置就好了。

二叉搜索树在理想状态下是平衡的，也就是说它的每层都被铺满，这样期望的树高是 (log(n)) 的，但是在极端情况下，它有可能退化成一条链，也就是 (n) 的。

现在有这样一组数据：1,2,3,4,5

假如你现在构建这样一棵二叉搜索树，你会发现它长成这个样子：

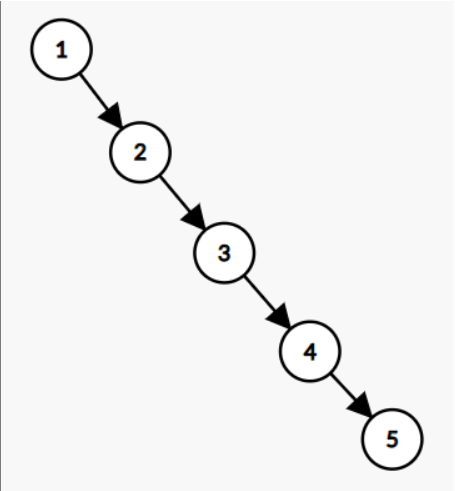
那么，如何保证这棵树是 (log(n)) 的树高呢？

这就是今天的主要课题：可以保证树高为 (log(n)) 的二叉搜索树，叫做平衡二叉搜索树，简称平衡树。

Part 2 Treap原理

平衡树的实现方法有很多，Treap（树堆） 是其中最易于实现的一种之一。

Treap 是 Tree（树）和 Heap（堆）的合并缩写，之所以这么叫，是因为它既满足 BIT 的性质，也满足堆的性质。

Treap 在维护 BIT 的性质的同时，维护一个堆（大小根堆都是可以的），其中 BIT 的关键字 value 是我们赋予它的，堆的关键字 key 是随机（利用 cstdlib 库中的 rand( ) 函数）赋值的。

似乎感觉这种随机操作很玄学？然而，正是 Treap 的这种随机性质，使得每个节点的位置被随时调整，从而可以保证整棵树的树高为期望 (log(n))（毕竟还是随机算法，不能保证严格的 (log(n)) ） 。但是在较大的数据面前，Treap 表现出的性能还是十分优秀的。除非你上辈子毁灭了世界，否则不用担心因为随机数而爆掉。

上面我提到（加粗）了“调整”这个词，没错，BIT 的形态是可以调整的。譬如 Part 1 中的那棵退化成链的 BIT 可以进行如下调整，调整之后，同样满足 BIT 的性质。

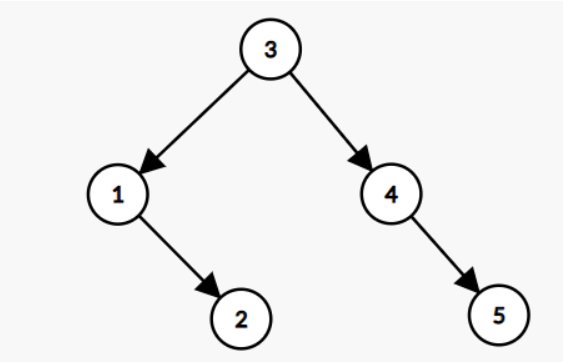
刚才说过，在 Treap 中，我们除了要维护它 BIT 的性质，还要维护它堆的性质，这就涉及到我们要调整每个节点在树中的层数位置，保证最大值或者最小值始终在堆顶。下面以小根堆 Treap 为例。

还记得堆中如何操作找到最小值吗？没错，就是交换相邻层节点，使得最小值不断“上浮”，最终到达堆顶。在 Treap 中，有另一种神奇的操作——旋转，可以在满足 BIT 的性质的情况下，交换两个节点的位置。

请看下面的图，我们借助这张图来详细分析一下。

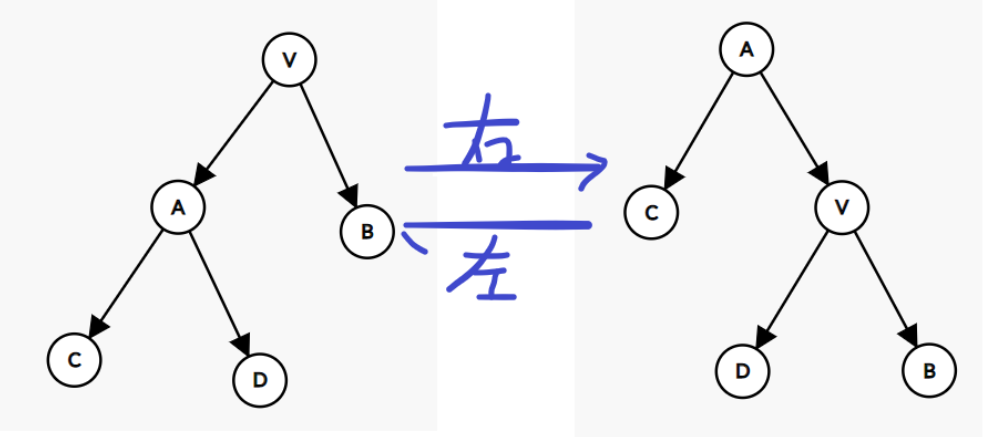
我们用一个数组 Val[x] 来表示节点 x 的权值，现在假设我们要交换 V 和 A 两个节点的位置。

根据 BIT 的性质，有： Val[C]<Val[A]<Val[D]< Val[V]<Val[B] 。

先不管那么多，直接交换 A 和 V 的位置一发，那么因为 Val[A]<Val[V]，V 势必要成为 A 的右儿子。此时，C 为 A 的左儿子，B 为 V 的右儿子不需要调整，剩下一个 D 节点，因为 Val[D]<Val[V] ，D 成为 V 的左儿子。

这样一番操作之后，我们就把原来在上方的节点 V 转到了它左儿子 A 的下方（右旋）。同样的，也可以把上方节点转到右儿子下方（左旋）。旋转可以维护 Treap 堆的性质，同时，有很多节点的左儿子或者右儿子是空的，这时，旋转就起到了调节树的形态的作用。（譬如 Part 1 中的链可以经过两次左旋达到它在 Part 2 中的形态）

Part 3 Treap 的作用、构建 Treap

Treap 支持向数据库中插入一个数，删除一个数，查询数据库内排名为 (k) 的元素，元素 (x) 的排名，比 (x) 大的最小的数或比 (x) 小的最大的数。所有这些操作的复杂度都是 (O(log(n))) 。

因为 C++ 的指针语法和平常使用的语文语法差不多，我习惯于使用指针写数据结构，现在来构建一棵 Treap。

首先，声明一个结构体：

struct Treap{
    int val,key,size,same;
    //val表示元素的值，key表示堆的关键字，size表示子树大小，same表示与当前元素相同的元素有几个
    Treap *ls,*rs;//表示左儿子，右儿子
    inline void update(){
        size=ls->size+rs->size+same;
    }//内联函数，用来更新自己的子树大小
};
struct Treap byte[maxn],*pool=byte,*root,*null;
//声明一个内存池，指向内存池的指针，根节点，空指针（null用来防止访问NULL而RE的状况

最重要的左右旋：

inilne void Turn_Right(Treap* &node){
	Treap *x=node->ls;//找到左儿子
	if(x==null)
		return;
	node->ls=x->rs;
	x->rs=node;
	x->size=node->size;
	node->update();//按照上面讲的方式修改左右儿子
	node=x;
}
inline void Left_turn(Treap *&node){
    Treap *x=node->rs;
    if(x==null)
    	return;
    node->rs=x->ls;
    x->ls=node;
    x->size=node->size;
	node->update();
    node=x;
}

如果您不习惯于使用指针，这里讲一下 C++ 指针的语法，如果您熟练掌握了指针，请跳过这一部分。

---

C++的每一个指针都指向一个内存，这个内存储存着一些数据。

对于这里的结构体指针 node ，它指向一块固定的内存 x ，我们可以用 node->？ 的语句，访问修改 x 中的成员。指针的赋值方式也很特别，node=p 这一句并不是用 p 指向的内存 x 覆盖掉 node 指向的内存 y ，而是让node 指向 p 指向的内存 x ，同时保留 y 。这也意味着之前指向 y 的其他指针包括 y 中成员的值不受影响。

如果您还没有明白，请自行画个图看看吧！

---

插入一个 value 值为 x 的元素：

和普通的 BIT 一样，我们需要递归寻找位置，然后在回溯的路上进行旋转调整，使得 Treap 满足堆的性质。

inline Treap* New(const int k){
    Treap *node=pool++;//在内存池中分配一个新的内存
    node->val=k;
    node->key=Rand();
    node->same=1;//初始相同元素只有1
    node->size=1;//子树大小只有1
    node->ls=node->rs=null;//左右儿子为空
    return node;
}
void Treap_insert(Treap* &node,int value){
    if(node==null){
        node=New(value);//找到空节点，那么新建
        return;
    }
    if(value==node->val)
        ++node->same;//找到一个相同的元素，same+1即可
    else if(value > node->val){//右插左旋，左插右旋，左小右大
        Treap_insert(node->rs,value);
        if(node->rs->key < node->key)
            Left_turn(node);//右儿子的key小于父节点的key，不满足小根堆堆的性质，左旋
    }else{
        Treap_insert(node->ls,value);
        if(node->ls->key < node->key)
            Right_turn(node);//同上，左儿子不满足堆的性质，右旋
    }
    node->update();//别忘了更新这个节点的子树大小
}

删除一个 value 值为 x 的元素：

和堆的删除方式一样，我们先递归操作，找到这个元素，然后把元素调整到叶子节点然后直接删除，不同的是，我们的调整方式是：左右旋。详见代码。

void Treap_delete(Treap* &node,int value){//删除键值为value的节点
    if(node==null)
        return;//如果找到了空节点，先返回
    if(node->val==value){//当前节点的值就是要找的值
        if(node->same>1){//如果相同的元素超过1，那么直接same--
            --node->same;
            node->update();//更新一下
            return;
        }
        if(node->ls==null && node->rs==null){
           node=null;//如果这个节点的左右儿子都为空，直接删除（指向空节点
           return;
        }else if(node->rs==null && node->ls)
            node=node->ls;//只有左儿子，那么左儿子继承node
        else if(node->ls==null && node->rs)
            node=node->rs;//只有右儿子，子承父业
        if(node->ls->key > node->rs->key){
            Left_turn(node);//把key值较小的节点上调
            Treap_delete(node->ls,value);//递归删除
        }else{
            Right_turn(node);
            Treap_delete(node->rs,value);
        }
    }else if(value>node->val)//还没找到等于 x 的节点，递归寻找
        Treap_delete(node->rs,value);
    else Treap_delete(node->ls,value);
    node->update();//别忘了更新
}

查询排名为 (k) 的元素：

从根开始递归，每次递归之前找到小于等于当前节点元素值的数的个数（也就是左子树大小+ same ），以此讨论该往左子树递归还是右子树递归。如果左子树中的数数量大于 (k) 个，说明所求元素在左子树中，向左子树递归，反之，说明所求元素比当前元素要大，向右子树递归。

int Get_kth(Treap* &node,int k){
    int tmp=node->ls->size+node->same;//表示小于等于node->val的数的个数
    if(node->ls->size<k && k<=tmp)
        return node->val;//这个数就是value
    else return node->ls->size >= k ? Get_kth(node->ls,k) : Get_kth(node->rs,k-tmp);
    //最小的有大于k个数，在左子树中寻找，直到缩小到k个数，否则减去左子树的大小，在右子树中寻找
}

查询 (x) 元素的排名：

和上面原理差不多，在比大小递归查找这个元素的同时，统计路径上左子树和 same 值的和即为答案。

int Get_rank(Treap* &node,int value){//找元素 value 的排名 
    if(node==null)
        return 0;//空节点不算
    if(node->val==value)
        return node->ls->size+1;//找到这个节点，那么左子树里的节点都比他小
    else return node->val < value ? node->ls->size + node->same + Get_rank(node->rs,value) : Get_rank(node->ls,value);
    //如果当前节点的值小于 value，在右子树里找，加上左子树和当前节点的same 
}

查询比 (x) 小的最大的数：

同上原理，利用 BIT 的性质查找即可。

void Get_pre(Treap* &node,int val){
    if(node==null)
        return;
    if(val>node->val)
        ans=node->val,Get_pre(node->rs,val);
        //如果当前节点的值小于x，更新答案，去右子树
    else
        Get_pre(node->ls,val);//当前节点比val大，那么去比当前节点更小的子树，不更新
}

查询比 (x) 大的最小的数：

同上原理，利用 BIT 的性质查找即可。

void Get_back(Treap* &node,int val){//查询比x大的最小的数
    if(node==null)
        return;
    if(val<node->val)
        ans=node->val,Get_back(node->ls,val);
    else
        Get_back(node->rs,val);
}

Part 4 完整代码仅供参考

#include<cstdio>
#include<iostream>
#include<cstdlib>

//using namespace std;

inline int read(){
    int x=0,fh=1;
    char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-')
            fh=-1;
        ch=getchar();
    }
    while(isdigit(ch)){
        x=(x<<3)+(x<<1)+ch-'0';
        ch=getchar();
    }
    return fh*x;
}

inline int Rand(){
    static int seed=114514; //seed可以随便取
    return seed=int(seed*48271LL%2147483647);
}//快速伪随机数

const int maxn=100005;
int n,ans;

struct Treap{
    int val,key,size,same;//
    Treap *ls,*rs;
    inline void update(){
        size=ls->size+rs->size+same;
    }
};
struct Treap byte[maxn],*pool=byte,*root,*null;
inline Treap* New(const int k){
    Treap *node=pool++;
    node->val=k;
    node->key=Rand();
    node->same=1;
    node->size=1;
    node->ls=node->rs=null;
    return node;
}
inline void Right_turn(Treap* &node){
    Treap *x=node->ls;
    if(x==null)
		return; 
    node->ls=x->rs;
    x->rs=node;
    x->size=node->size;
	node->update();
    node=x;
}
inline void Left_turn(Treap *&node){
    Treap *x=node->rs;
    if(x==null)
    	return;
    node->rs=x->ls;
    x->ls=node;
    x->size=node->size;
	node->update();
    node=x;
}
void Treap_insert(Treap* &node,int value){
    if(node==null){
        node=New(value);
        return;
    }
    if(value==node->val)
        ++node->same;
    else if(value > node->val){//右插左旋，左插右旋，左小右大
        Treap_insert(node->rs,value);
        if(node->rs->key < node->key)
            Left_turn(node);
    }else{
        Treap_insert(node->ls,value);
        if(node->ls->key < node->key)
            Right_turn(node);
    }
    node->update();
}
void Treap_delete(Treap* &node,int value){//删除键值为value的节点
    if(node==null)
        return;
    if(node->val==value){
        if(node->same>1){
            --node->same;
            node->update();
            return;
        }
        if(node->ls==null && node->rs==null){
           node=null;
           return;
        }else if(node->rs==null && node->ls)
            node=node->ls;
        else if(node->ls==null && node->rs)
            node=node->rs;
        if(node->ls->key > node->rs->key){
            Left_turn(node);
            Treap_delete(node->ls,value);
        }else{
            Right_turn(node);
            Treap_delete(node->rs,value);
        }
    }else if(value>node->val)
        Treap_delete(node->rs,value);
    else Treap_delete(node->ls,value);
    node->update();
}
int Get_rank(Treap* &node,int value){//找元素 value 的排名 
    if(node==null)
        return 0;
    if(node->val==value)
        return node->ls->size+1;//找到这个节点，那么左子树里的节点都比他小
    else return node->val < value ? node->ls->size + node->same + Get_rank(node->rs,value) : Get_rank(node->ls,value);
    //如果当前节点的值小于 value，在右子树里找，加上左子树和当前节点的same 
}
int Get_kth(Treap* &node,int k){
    int tmp=node->ls->size+node->same;//表示小于等于node->val的数的个数
    if(node->ls->size<k && k<=tmp)
        return node->val;
    else return node->ls->size >= k ? Get_kth(node->ls,k) : Get_kth(node->rs,k-tmp);
    //最小的有大于k个数，在左子树中寻找，直到缩小到k个数，否则减去左子树的大小，在右子树中寻找
}
void Get_pre(Treap* &node,int val){//查询比x小的最大的数
    if(node==null)
        return;
    if(val>node->val)
        ans=node->val,Get_pre(node->rs,val);//记录当前节点的值为答案，去比当前节点更大的子树
    else
        Get_pre(node->ls,val);//当前节点比val大，那么去比当前节点更小的子树
}
void Get_back(Treap* &node,int val){//查询比x大的最小的数
    if(node==null)
        return;
    if(val<node->val)
        ans=node->val,Get_back(node->ls,val);
    else
        Get_back(node->rs,val);
}
signed main(){
	//freopen("P3369_2.in","r",stdin);
    null=New(0);
    null->size=null->same=0;
    root=null;
    n=read();
    for(int i=0,opt;i<n;i++){
        opt=read();
        if(opt==1)
            Treap_insert(root,read());
        if(opt==2)
            Treap_delete(root,read());
        if(opt==3)
            printf("%d
",Get_rank(root,read()));
        if(opt==4)
            printf("%d
",Get_kth(root,read()));
        if(opt==5){
            Get_pre(root,read());
            printf("%d
",ans);
        }
        if(opt==6){
            Get_back(root,read());
            printf("%d
",ans);
        }
        //printf("value %d same %d size %d
",root->val,root->same,root->size);
    }
    return 0;
}