Part 1 普通并查集与基本优化
并查集能干什么?
并查集,顾名思义,其实就是维护了所有元素中每一个元素的所属集合是谁
譬如设序列(a=){1,2,3,4,5},假设1,2属于一个集合,3,4属于一个集合,5自己一个集合
那么这个序列就可以表示成这样:{{1,2},{3,4}{5}},其中属于一个集合的元素已经用花括号括起来了
并查集的主要功能是维护一个序列和若干个集合,快速查询两个元素是不是属于同一个集合、合并两个集合
并查集的原理是什么
并查集使用了树形结构(森林)来维护,使用数组fa[i]来维护第i个元素的父亲是谁,也就代表i和fa[i]属于同一个集合,此时这棵树上的所有节点就是这个集合的所有元素
比如还是维护刚才的序列(a),初始时所有的元素都自己构成一个集合,那么森林大概是这样的:
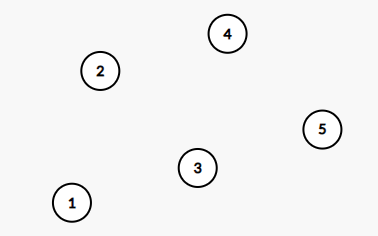
(我会用Graph Editor辣!)
现在考虑合并两个元素所在的集合,假设合并(1,2),那么fa[1]=2;,(或fa[2]=1;),同理合并3和4,把这种父子关系抽象成有向边,那么森林是这样的
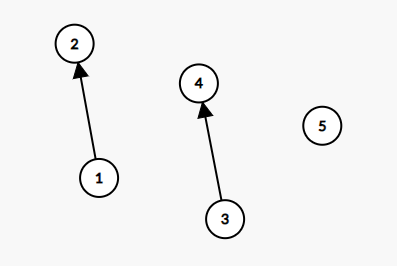
现在考虑合并{(1,2)}和{(3,4)}所在集合,如果还是直接fa[3]=2;的话,那么会造成这种结果:

看到原来的fa[3]是4,此时4被覆盖掉了。这样森林中维护1,2,3属于同一集合,但实际上4也应该和1,2,3属于同一集合
此时的做法是:找到包含3的这棵树的根节点,此时根节点没有父亲(是他自己),那么可以把这个根节点的父亲指向2,这样就不会造成错误了

#include<cstdio>
using namespace std;
#define maxn 100005
int fa[maxn];
//寻找根节点代码
inline int Find(const int x){
if(fa[x]==x) return x;//父亲是自己,说明是根节点,返回
return Find(fa[x]);//递归继续寻找父亲的父亲
}
//合并代码
inline void Merge(const int x,const int y){
fa[Find(x)]=Find(y);//把x的根节点的父亲记为y
}
优化复杂度
恭喜你,现在已经会使用并查集了,但是你发现交到并查集的板子题上却TLE了,疑惑的你不得不考虑优化
为什么复杂度会爆炸呢?
如果使用纯粹的树上记录,我们在查询树根的时候需要从一个点一步一步向上跳,这使得我们的复杂度提高了
比如上面这个图,假设我们要查3号节点的根,那么需要跳两次,对于更极端的情况,复杂度会达到接近(O(n))
那么怎么办呢?有一个最最方便的优化方法——路径压缩法,假设我们现在的并查集是这样的:
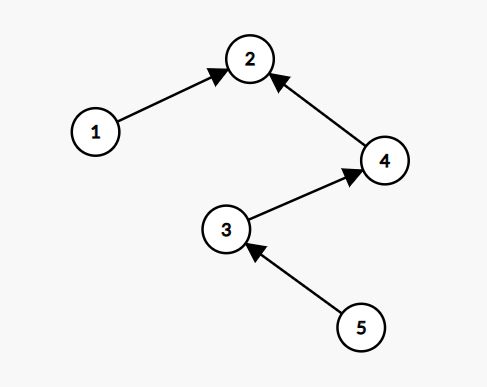
对于上面这个图,经过路径压缩后的形态就是这样
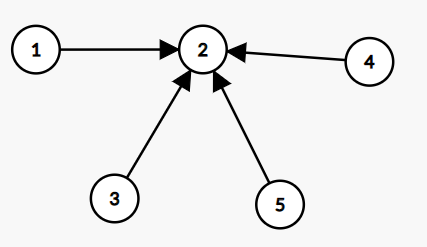
可以看到,每个儿子的父节点都被直接修改成了根节点,这样以后再访问的时候,复杂度就是(O(1))了
这么做的时间复杂度在最坏情况下是(O(logn))的,但是因为没有人会特意构造数据卡并查集,所以在使用时可以近似认为是一个小常数
为什么说这个方法非常方便呢?因为它实现起来根本不费吹灰之力:
以下是代码
inline int Find(const int x){
if(fa[x]==x) return x;
return /*fa[x]=*/Find(fa[x]);
//上面那句注释掉的部分就是路径压缩
//其他部分和普通并查集是一模一样的
}
Part 2:更多功能的普通并查集
如何让并查集满足更多需求?
比如我们需要满足分组,并且维护这几组中元素的关系,就需要用到多功能并查集:
题目中要求我们根据A->B->C->A的关系,判断给出的话是真话还是假话
因为对于每一个物种,都有且只有一类动物是天敌,有且只有一类动物是猎物,有且只有一类动物是同类
那么我们可以考虑开3倍空间的并查集,1倍存天敌是哪些动物,2倍存同类是哪些动物,3倍存猎物是哪些动物
合并的时候,就把一个动物的所有同类/天敌/猎物合并到一起,得以维护他们之间的关系
(Code)
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<iomanip>
#include<cstring>
#include<utility>
#include<cstdio>
#include<queue>
#include<stack>
#include<ctime>
#include<cmath>
#include<list>
#include<set>
#include<map>
typedef long long int ll;
inline int read(){
int fh=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-') fh=-1;ch=getchar(); }
while('0'<=ch&&ch<='9'){ x=(x<<3)+(x<<1)+ch-'0';ch=getchar(); }
return fh*x;
}
inline int _abs(const int x){ return x>=0?x:-x; }
inline int _max(const int x,const int y){ return x>=y?x:y; }
inline int _min(const int x,const int y){ return x<=y?x:y; }
inline int _gcd(const int x,const int y){ return y?_gcd(y,x%y):x; }
inline int _lcm(const int x,const int y){ return x*y/_gcd(x,y); }
#define maxn 50005
#define inf 0x3f3f3f3f
int fa[maxn*4];//为了方便理解,我开了4倍空间
//一倍存天敌,二倍存同类,三倍存猎物
inline int Find(const int x){
if(x==fa[x]) return x;
return fa[x]=Find(fa[x]);
}
inline void Merge(const int x,const int y){
fa[Find(x)]=Find(y);
}
int n,k,fake;
int main(){
n=read(),k=read();
for(int i=n;i<=n*4+10;i++)
fa[i]=i;//初始化并查集
for(int i=1;i<=k;i++){
int op=read(),x=read(),y=read();
if((x==y)&&op==2){
fake++;
continue;
}
if(x>n||y>n){
fake++;
continue;
}
if(op==1){//x和y是同类
if(fa[Find(x+n*2)]==fa[Find(y+n*3)]||fa[Find(y+n*2)]==fa[Find(x+n*3)]) fake++;//x和y不是同类
else{
Merge(x+n*2,y+n*2);//x的同类也是y的同类
Merge(x+n*3,y+n*3);//x的猎物也是y的猎物
Merge(x+n,y+n);//x的天敌也是y的天敌
}
}else{//x吃y
if(fa[Find(y+n*3)]==fa[Find(x+n*2)]||fa[Find(x+n*2)]==fa[Find(y+n*2)]) fake++;//y吃x或者x和y是同类,那么这句话是假话
else{//x->y->z->x
Merge(x+n,y+n*3);//y的猎物是x的天敌
Merge(x+n*3,y+n*2);//x的猎物是y的同类
Merge(x+n*2,y+n);//x的同类是y的天敌
}
}
}
printf("%d",fake);//输出假话总数
return 0;
}