吐槽:严格次小生成树我调了将近10个小时……(虽然有3个小时的电竞时间
Part 1:最小生成树(Kruskal)算法
前言
介于我们之前已经讨论过最小生成树的定义和(Prim)算法了,这次我们直奔主题——(Kruskal)算法
(Kruskal)算法工作方式
还是老样子,我们抛开正确性不谈,只谈算法工作方式和代码实现
(Kruskal)的思路非常暴躁:把每个点看成是一个单独的连通块,然后把边按照边权排序,从小到大一条一条加入最小生成树,这样直到有(n-1)条边被加入了最小生成树
注意每次加入边的时候,至少有原来不连通的两连通块被联通,这样才能够保证不会形成环
为什么不满足上面的条件就会形成环?
显然易见,如果两个点在加入这条边之前,已经可以相互到达了(成为一个连通块),那么这条边就是多余的,在连接之后会形成重边或者环
每一个连通块都是一个无根树,在树上任意两点之间加一条边,一定会形成一个环,所以为了不形成环,我们不加这条边
让我们举一个生动形象的例子(因为电脑画图实在不方便,这里改成手画了)
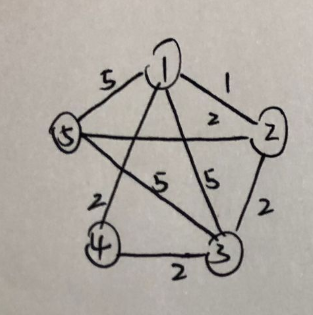
比如像上面这张带权无向图:
我们模拟(Kruskal),每个点全都分开,从小到大加入边

重复这个操作一直从小到大的加边,直到完成最小生成树

然后这样我们就得到了这个图的最小生成树(不唯一),它的大小为(7)
(Kruskal)算法实现方式
在算法中,有一个很重要的步骤,就是维护每一条边连通的两个点是不是处于同一个连通块之内,如果处于同一连通块之内,那么这条边是不能被加入最小生成树的
所以我们需要一种数据结构来维护各个连通块的情况,而并查集就很好的满足了我们的要求
PS:不知道什么是并查集?请戳这里
维护一个有(n)个集合(每个集合代表一个点)的并查集,初始时每个集合中只有一个元素(点(i))
(1、)对于每次加边之前,查询两个端点(a,b)是否在同一集合里,如果不在同一集合里,执行(2),如果在同一集合,那么说明(a,b)已经连通了,跳过这条边
(2、)把这条边计入最小生成树,然后合并点(a,b)所在的集合
(Code)
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<algorithm>
#include<set>
#include<map>
#include<utility>
#include<iostream>
#include<list>
#include<ctime>
#include<cmath>
#include<cstdlib>
#include<iomanip>
typedef long long int ll;
inline int read(){
int fh=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-') fh=-1;ch=getchar(); }
while('0'<=ch&&ch<='9'){ x=(x<<3)+(x<<1)+ch-'0';ch=getchar(); }
return fh*x;
}
inline int _abs(const int x){ return x>=0?x:-x; }
inline int _max(const int x,const int y){ return x>=y?x:y; }
inline int _min(const int x,const int y){ return x<=y?x:y; }
inline int _gcd(const int x,const int y){ return y?_gcd(y,x%y):x; }
inline int _lcm(const int x,const int y){ return x*y/_gcd(x,y); }
const int maxn=5005;
const int inf=1e9;
int n,m;
struct Edge{
int a,b,w;
Edge(){}
}edge[200005];//建立一个结构体,存边的两个端点和权值
bool operator < (const Edge p,const Edge q){ return p.w<q.w; }
//重载运算符,按照权值从小到大排序
int fa[maxn];
int find(const int x){
if(fa[x]==x) return x;
return fa[x]=find(fa[x]);
}//并查集的查询操作,查询x的集合代表
inline int Kruskal(){
int ans=0;//最小生成树大小
std::sort(edge,edge+m);//排个序
for(int i=1;i<=n;i++)//并查集初始化,每个点都是独立的连通块
fa[i]=i;
for(int i=0;i<m;i++){//把所有边扫一遍
int x=edge[i].a,y=edge[i].b;
if(find(x)==find(y)) continue;//如果属于一个集合,就跳出
fa[find(x)]=y;//合并两个集合
ans+=edge[i].w;//统计最小生成树大小
}
return ans;
}
int main(){
n=read(),m=read();
for(int i=0,x,y,z;i<m;i++){
x=read(),y=read(),z=read();
if(x==y) continue;
edge[i].a=x;
edge[i].b=y;
edge[i].w=z;//建图
}
printf("%d
",Kruskal());//跑最小生成树
return 0;
}
Part 2:求解(严格)次小生成树
传送门:【模板】严格次小生成树
什么是次小生成树
字面意思来讲,次小生成树就是除了最小生成树之外最小的那棵生成树
那么为什么把“严格”加了个括号呢?因为它并不严格(废话)
如果最小生成树选择的边集是(E_M),严格次小生成树选择的边集是(E_S),那么需要满足:((value(e))表示边(e)的权值())
(sum_{e in E_M}value(e)<sum_{e in E_S}value(e))
显然这个公式它比较恶心,简单来说,就是次小生成树的大小必须严格小于最小生成树的大小
如果我们只是在最小生成树上更换了边,但是总的生成树大小一样,那么求出的就是不严格的次小生成树(因为一张图的最小生成树可以有多个,此时求出了另一个最小生成树)
求严格次小生成树(思路篇)
看到“严格次小生成树”,你的第一反应应该是“这个东西会和最小生成树有关!”
所谓“次小”就是除了最小之外的最小的,那么我们先求出最小的,起码不会对我们的求解起阻碍作用吧
假设你已经顺手使用(Prim)或者(Kruskal)算法求出了这张图的最小生成树
现在,我们可以把这个图上的所有边简单的分成两类了——第一类是在最小生成树上的边(简称树边),第二类是不在最小生成树上的边(简称非树边)
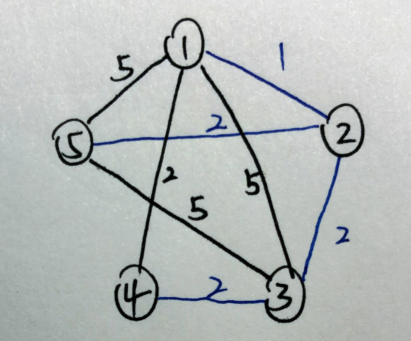
还是一开始的那个图,最小生成树上的边使用蓝笔标出,我们已知这个最小生成树的大小(size=7)
可以贪心的转化问题——求第二小,也就是求一个新的生成树大小(size')在比(size)小的前提下最大
因为严格次小生成树和最小生成树一定不是同一棵树,那么我们可以考虑用一些非树边,替换掉同等数量的树边
想到替换时,也许你会遇到这些问题,(以下用三元组((a,b,c))表示连通(a、b)两点的边,权值为(c))
1. 替换时,怎么保证求出的是(2)小而不是(3)小、(4)小、(n)小呢?
根据上面的贪心思路:替换后使得(size'-size)最小,那么(size')就是严格次小生成树
2. 一条非树边可以替换掉哪些树边?
显然不可以胡乱替换,因为需要保证求出的次小生成树还有个树的模样(不能出现环、必须连通)
想到利用树的性质:当我们要向一棵树中加入一条边时,会形成且仅形成一个环,并且这个环包含(a ightarrow LCA(a,b))和(b ightarrow LCA(a,b))路径中的所有边
我们先把一条非树边((a,b,c))加进去,在(a ightarrow LCA(a,b))和(b ightarrow LCA(a,b))路径中的边中删除一条即可保证树的性质
上面的解释理解不能?请看下面的图,帮助理解:
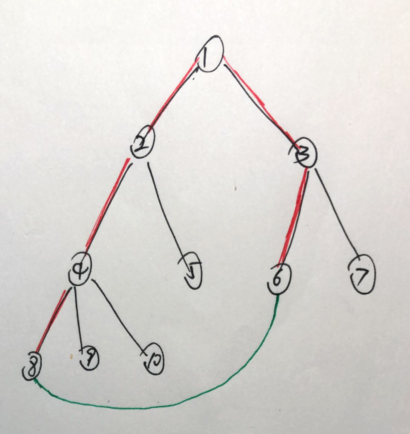
如图,黑色的是树边,现在要把一条绿色的非树边((8,6,n))加进去,那么图中标红的树边就可以被替换
书面证明
对于一棵树(T)其中任意两个节点(a,b)都存在且仅存在一条简单路径:(a ightarrow LCA(a,b) ightarrow b)
现在连接((a,b)),那么上式可以写成这样:(a ightarrow LCA(a,b) ightarrow b ightarrow a),显然构成一个环
PS:另外,因为连接((a,b))之前路径只有一条,所以连接后,形成的环也只有一个
证毕
3. 用几条非树边替换几条树边呢?
在解决这个问题之前,先给出另一个结论:
对于任意一条非树边((a,b,c)),在把它加入最小生成树后形成的环中,每一条树边的权值(wleq c)
解决这个问题,需要用到这个结论,所以我们先来证明一下它
证明
设加入的非树边是((a,b,c)),产生环包含树边的集合是(T),(w_e)表示(e)的边权,最小生成树的大小为(size)
反证法:
设(p:exists ein T)且有(w_e>c)
假设(p)为真,那么此时断掉树边(e),加入非树边((a,b,c))会使得(size)减小
但是(size)是我们所求出的最小生成树的大小,它不可能更小了,所以(p)为假
那么(!p:forall ein T w_eleq c)一定为真
证毕
有了上面的结论还不够,要想继续解决这个问题,我们还得大胆猜想,小心求证
做出假设:替换(1)条边最优
证明
还记得我们的贪心思路吗:替换后使得(size'-size)最小,那么(size')就是严格次小生成树
我们假设用一条非树边(e_1)去替换一条树边,运用上面的结论,我们知道所有与(e_1)构成环的边的权值(wgeq w_{e_1})
如果我们做这次替换,(size')的大小就会比(size)大(k=w-w_{e_1})
考虑特殊情况,(k=0)时,代表着我们把两条权值相等的树边和非树边做了替换
但是这么做对(size')没有任何影响,只对次小生成树的形态有影响,但它长得好不好看我们并不关心,我们只关心(size')而已
因为(k=0)时,对(size')没有影响,排除这种情况,现在(k)的范围((k>0))
(注意我们以后都不再考虑(k=0)的情况了!!!)
显然我们选择(n)条边,就会产生多个(k)值,此时(size')一定大于只选(1)条边的(size')
根据贪心思路,要求(size')最小,显然选(1)条边做替换最优
证毕
问题解决,选择(1)条边做替换最优(也就是最小生成树和次小生成树中权值不相同的边有且只有(1)条)
4. 用哪条非树边替换哪条树边?答案怎么更新?
这两个我们逃不掉得枚举其中一个了,这里显然枚举非树边比较方便(设树边边权为(w))
因为我们要求(size')最大的,所以要求((c-w>0))且((c-w))尽量小,因为(c)一定,只要使得(w)尽量大即可(注意这里根据上面的结论,(cgeq w)所以不用担心(c-w<0)的情况)
枚举每一个非树边((a,b,c)),找到路径(a ightarrow LCA(a,b))和(b ightarrow LCA(a,b))中(w)最大的那条边,做替换即可,答案就是(size'=min(size',size+c-w))
注意一下小细节:因为(w)有可能等于(c),如果做替换的话,求出的并不是严格次小生成树,所以还需要记录一个次大值(w'),如果(w=c),那么答案(size'=min(size',size+c-w'))
啰啰嗦嗦这么多,按照上面的思路,就可以求严格次小生成树了
求严格次小生成树(实现篇)
明确了思路,有没有感到干劲十足呢?(必须得干劲十足啊,笔者可是(1)小时写完,(7)小时(debug)的男人)
这里梳理一下我们要用的算法和数据结构吧:
1. 求最小生成树:并查集,(Kruskal),无脑存边
2. 最近公共祖先(LCA):树上倍增,(dfs)预处理,邻接表
3. 区间最大/次大(RMQ):树上(st)表
4. 一句提醒:不开(long) (long)见祖宗
所以得到公式:基础算法+数据结构+简单证明=毒瘤题(这题其实出的挺好的,既没超纲,又有一定难度)
大体框架有了,剩下的都是代码实现的细节了,就都在代码注释里讲解吧
求严格次小生成树(代码篇)
#include<cstdio>
#include<cstring>
#include<queue>
#include<stack>
#include<algorithm>
#include<set>
#include<map>
#include<utility>
#include<iostream>
#include<list>
#include<ctime>
#include<cmath>
#include<cstdlib>
#include<iomanip>
typedef long long int ll;
inline int read(){
int fh=1,x=0;
char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-') fh=-1;ch=getchar(); }
while('0'<=ch&&ch<='9'){ x=(x<<3)+(x<<1)+ch-'0';ch=getchar(); }
return fh*x;
}
inline int _abs(const int x){ return x>=0?x:-x; }
inline ll _max(const ll x,const ll y){ return x>=y?x:y; }
inline ll _min(const ll x,const ll y){ return x<=y?x:y; }
inline int _gcd(const int x,const int y){ return y?_gcd(y,x%y):x; }
inline int _lcm(const int x,const int y){ return x*y/_gcd(x,y); }
const int maxn=100010;
const ll inf=1e18;//赋个极大值
int n,m;
ll MST,ans=inf;//ans是次小生成树,MST是最小生成树
struct Node{
int to;//到达点
ll cost;//边权
};
std::vector<Node>v[maxn];//邻接表存最小生成树
int dep[maxn];//dep[i]表示第i个点的深度
bool vis[maxn];
ll f[maxn][25];//f[i][j]存节点i的2^j级祖先是谁
ll g1[maxn][25];//g1[i][j]存节点i到他的2^j级祖先路径上最大值
ll g2[maxn][25];//g2[i][j]存节点i到他的2^j级祖先路径上次大值
void dfs(const int x){//因为是树上st和树上倍增,所以可以一起预处理
vis[x]=true;//x号点访问过了
for(int i=0;i<v[x].size();i++){//扫所有出边
int y=v[x][i].to;
if(vis[y]) continue;//儿子不能被访问过
dep[y]=dep[x]+1;//儿子的深度是父亲+1
f[y][0]=x;//儿子y的2^0级祖先是父亲x
g1[y][0]=v[x][i].cost;//y到他的2^0级祖先的最大边长
g2[y][0]=-inf;//y到他的2^0级祖先的次大边长(没有次大边长,故为-inf)
dfs(y);//递归预处理
}
}
inline void prework(){//暴力预处理
for(int i=1;i<=20;i++)//枚举2^1-2^20
for(int j=1;j<=n;j++){//枚举每个点
f[j][i]=f[f[j][i-1]][i-1];//正常的倍增更新
g1[j][i]=_max(g1[j][i-1],g1[f[j][i-1]][i-1]);
g2[j][i]=_max(g2[j][i-1],g2[f[j][i-1]][i-1]);
//以下是求次大的精华了
if(g1[j][i-1]>g1[f[j][i-1]][i-1]) g2[j][i]=_max(g2[j][i],g1[f[j][i-1]][i-1]);
//j的2^i次大值,是j的2^(i-1)和j^2(i-1)的2^(i-1)最大值中的较小的那一个
//特别的,如果这两个相等,那么没有次大值,不更新g2数组
else if(g1[j][i-1]<g1[f[j][i-1]][i-1]) g2[j][i]=_max(g2[j][i],g1[j][i-1]);
}
}
inline void LCA(int x,int y,const ll w){
//非树边连接x,y权值为w
//求LCA时候直接更新答案
ll zui=-inf,ci=-inf;//zui表示最大值,ci表示次大值
if(dep[x]>dep[y]) std::swap(x,y);//保证y比x深
for(int i=20;i>=0;i--)//倍增向上处理y
if(dep[f[y][i]]>=dep[x]){
zui=_max(zui,g1[y][i]);//更新路径最大值
ci=_max(ci,g2[y][i]);//更新路径次大值
y=f[y][i];
}
if(x==y){
if(zui!=w) ans=_min(ans,MST-zui+w);//如果最大值和w不等,用最大值更新
else if(ci!=w&&ci>0) ans=_min(ans,MST-ci+w);//有毒瘤情况,没有次大值,此时也不能用次大值更新
return;
}
for(int i=20;i>=0;i--)
if(f[x][i]!=f[y][i]){
zui=_max(zui,_max(g1[x][i],g1[y][i]));
ci=_max(ci,_max(g2[x][i],g2[y][i]));
x=f[x][i];
y=f[y][i];
}//依旧是普通的更新最大、次大值
zui=_max(zui,_max(g1[x][0],g1[y][0]));//更新最后一步的最大值
//注意下面这两句又凝结了人类智慧精华
//因为次大值有可能出现在最后一步上,所以在更新答案前还要更新一下ci
//如果最后两边的某一边是最大值,ci就只能对另一边取max
if(g1[x][0]!=zui) ci=_max(ci,g1[x][0]);
if(g2[y][0]!=zui) ci=_max(ci,g2[y][0]);
if(zui!=w) ans=_min(ans,MST-zui+w);
else if(ci!=w&&ci>0) ans=_min(ans,MST-ci+w);//依旧特判毒瘤情况
}
struct Edge{
int from,to;//连接from和to两个点
ll cost;//边权
bool is_tree;//记录是不是树边
}edge[maxn*3];
bool operator < (const Edge x,const Edge y){ return x.cost<y.cost; }
//重载运算符,按照边权从大到小排序
int fa[maxn];//并查集数组
inline int find(const int x){
if(fa[x]==x) return x;
else return fa[x]=find(fa[x]);
}//查询包含x的集合的代表元素
inline void Kruskal(){
std::sort(edge,edge+m);//先排序
for(int i=1;i<=n;i++)//初始化并查集
fa[i]=i;
for(int i=0;i<m;i++){
int x=edge[i].from;
int y=edge[i].to;
ll z=edge[i].cost;
int a=find(x),b=find(y);
if(a==b) continue;//如果x和y已经连通,continue掉
fa[find(x)]=y;//合并x,y所在集合
MST+=z;//求最小生成树
edge[i].is_tree=true;//标记为树边
v[x].push_back((Node){y,z});//邻接表记录下树边
v[y].push_back((Node){x,z});
}
}
int main(){
n=read(),m=read();
for(int i=0,x,y;i<m;i++){
ll z;
x=read(),y=read();scanf("%lld",&z);
if(x==y) continue;
edge[i].from=x;
edge[i].to=y;
edge[i].cost=z;
}//读入整个图
Kruskal();//初始化最小生成树
dep[1]=1;//设1号点是根节点,把它变成有根树
dfs(1);//从1开始预处理
prework();//倍增预处理
for(int i=0;i<m;i++)//枚举所有边
if(!edge[i].is_tree)//如果是非树边,那么更新答案
LCA(edge[i].from,edge[i].to,edge[i].cost);
printf("%lld
",ans);//输出答案,不开long long见祖宗
return 0;//我谔谔终于结束
}
不严格次小生成树
严格的都说了,那就再稍微说一两句不严格次小生成树的求法
刚才那么多的证明,就是为了让这个不严格变成严格,现在我们倒过来看,这个问题就变得小儿科了
整体框架不用变,只是我们不需要处理次大值了,每次更新的时候直接(ans=min(ans,ans+c-w);)即可