双向(折半)搜索
Part 1:双向搜索概念与朴素复杂度分析
双向搜索是对于深度优先搜索的一种优化,它的基本思想是:把(dfs)从一端开始改为从两端开始,从而有效减少搜索状态
如果上面的定义不懂的话,请看下面两这张图(设(n)是搜索层数):
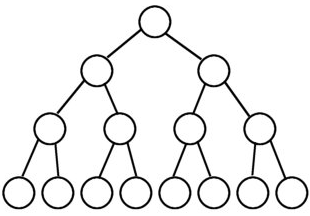
上面这个图就是普通的(dfs)在每次拓展两个节点的情况下所产生的的搜索树的形状
这棵搜索树,每一个节点都代表了一次递归调用,我们很容易可以看出来它的复杂度是(O(2^n))(满二叉树情况下)(其实减不减1无所谓了)
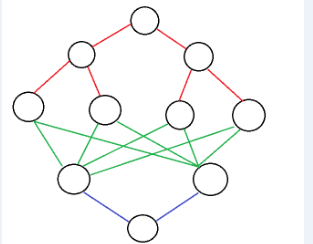
下面这个是双向搜索所产生的两棵搜索树(一颗红色,一颗蓝色)
我们在这两棵搜索树上分别得到了(4)和(2)种结果,现在组合一下(绿色部分),得到了(4*2=8)种结果,和原来的搜索结果一样
那么分析复杂度:我们一次搜索的复杂度(O(2^frac{n+2}{2})),两次搜索就是(O(2^{frac{n+4}{2}}))
如果我们朴素的统计答案,那么一次搜索会产生(2^{frac{n}{2}})种结果,两次则平方,变成了(2^n)次统计
把复杂度相加:总复杂度是(O(2^{frac{n+4}{2}}+2^n))
Q:怎么还慢了呢?混蛋!
A:(没错就是慢了)
Q:那你讲个P!(握紧小拳头)
A:(先别打,先别打!我还没讲完呢!)
Part 2:真正的双向搜索复杂度分析
上面的方法慢了,主要原因是我们选择了“朴素”的统计答案
考虑怎么优化:我们统计答案的第一步就是判断这个组合得到的最终答案合不合法
那么,我们可以考虑对其中一个答案数组排序,然后以另一个答案数组为查找元素进行二分查找
假设找到一个元素,因为在它之前的元素一定小于它,所以在这个元素之前的元素也都合法,这样我们就不用一个一个的统计答案了,提高了效率
分析这么做的时间复杂度:
(sort())快速排序一遍(O(frac{n}{2}logn))
进行(frac{n}{2})次二分查找,(O(frac{n}{2}logn))
统计答案总复杂度:(O(nlogn))
算法总复杂度:(O(2^{frac{n+4}{2}}+nlogn))
这不就快了吗
Part 3:例题
传送门:https://www.luogu.com.cn/problem/P4799
题目中要求我们求出在不超过总预算的情况下,小B去看比赛的方案数
首先,数据范围(nleq 40),普通的(dfs)肯定会(TLE)的飞起,我们考虑双向搜索
令(Mid=frac{n}{2}),我们第一次从(1)搜索到(Mid),把答案记录到序列(a)中,第二次从(Mid+1)搜索到(n)答案记录到序列(b)中
现在统计答案,从(a),(b)中任选一个序列进行快速排序,(这里排哪个应该对时间有影响,但是不大),这里假设我们对(b)排序
我们的满足答案的状态是:(a_i+b_j<=m),所以我们对(a)数组(for)一遍,在(b)数组中二分查找第一个大于(m-a_i)的元素
假设第一个大于(m-a_i)的元素是(b_j),那么在(j)之前的元素一定也符合条件(因为(b)序列单调不降),于是(ans+=j)
另外,因为我们搜索时会进行一些特判和剪枝,所以我们搜索和统计答案的复杂度比上面推出来的式子低,总复杂度也远远低于(O(2^{frac{n+4}{2}}+nlogn))
(Code)
#include<cstdio>
#include<utility>
#include<algorithm>
typedef long long int ll;
const ll maxn=(1<<20)+10;//产生的最大状态数是2^20
ll n,m,price[45],ida,idb,a[maxn],b[maxn],ans;//不开long long见祖宗
//n场比赛,m预算,price[i]表示第i场收费,ida为a数组的迭代器,idb是b数组的迭代器,ans统计答案
inline ll read(){
ll x=0,fh=1;
char ch=getchar();
while(ch<'0'||ch>'9'){ if(ch=='-') fh=-1;ch=getchar(); }
while('0'<=ch&&ch<='9'){ x=(x<<3)+(x<<1)+ch-'0';ch=getchar(); }
return x*fh;
}//瞎写的快读
void dfs(ll num,ll u,ll end,ll turn){
//num表示枚举到第num场比赛,u表示已使用预算,end表示搜到第几场比赛停止,turn表示这是第几轮搜索
if(num==end+1){//如果搜到了end+1场比赛,则已经完成搜索,记录答案
if(turn==1){ a[ida]=u;ida++; }//第一轮记录到a中,迭代器++
else{ b[idb]=u;idb++; }//第二轮记录到b中迭代器++
return;
}
dfs(num+1,u,end,turn);//第num场比赛不看
if(u+price[num]<=m)//剪枝,如果要看第num场比赛,那么先判断钱够不够,不够的话看个寂寞,直接跳过搜索
dfs(num+1,u+price[num],end,turn);
}
int main(){
n=read(),m=read();
for(ll i=1;i<=n;i++)
price[i]=read();//快速读入
ll Mid=(n>>1);//取中点Mid
dfs(1,0,Mid,1);//第一次搜索
dfs(Mid+1,0,n,2);//第二次搜索
std::sort(b,b+idb);//对b序列排序
for(ll i=0;i<ida;i++){
ll qwq=std::upper_bound(b,b+idb,m-a[i])-b;
//在b中二分查找第一个大于n-a[i]的元素
ans+=qwq;//答案加上该元素的下标,分析如上
}
printf("%lld
",ans);//输出答案
return 0;
}
感谢您的阅读(OvO)