坐标系
- 坐标系的简介
- 坐标系和图形
- 坐标系和视觉通道
- 坐标系的变化
- 坐标系的接口设计
- 更多
坐标系的简介
前面的章节中我们介绍过了视觉通道,视觉通道中识别度最高,同时支持定性(分类)数据和定量数据的视觉通道是位置(position)。各种几何标记最大的差异就在于数据空间位置的映射,我们将这个空间定义成坐标系。常见的坐标系:
- 直角坐标系(笛卡尔坐标系),有几个互相垂直的向量构成的空间,G2中当前实现的是x,y两个基底向量构成的二维直角坐标系,三维坐标系后面的版本中提供。
- 极坐标系,是使用一个角度值和长度值构成的坐标系,使用x轴表示角度,y轴表示半径的长度。
- 质心坐标系,使用三角形的三个顶点求得坐标点 u,v,w,且w = 1-u-v,这个坐标系在三维绘图中广泛使用。
G2中主要实现了直角坐标系和极坐标系,坐标系主要完成了两个功能:
- 将 0-1 区间内的数据映射到画布空间
- 将画布空间的数据,翻转回0-1的范围内
实现的坐标系
- rect 直角坐标系,目前仅支持二维
- polar 极坐标系,角度和半径构建成的二维坐标系
- plus 一种存在空心的极坐标系,半径不是从圆心开始,构建出来的坐标系
- theta 一种特殊的极坐标系,半径长度固定,仅仅将数据映射到角度,常用于实现饼图
- map 地图相关的坐标系,地图需要将球形上的数据映射到二维平面上,所以会提供一些投影算法,这个坐标系我们在 地图章节中详细的介绍。
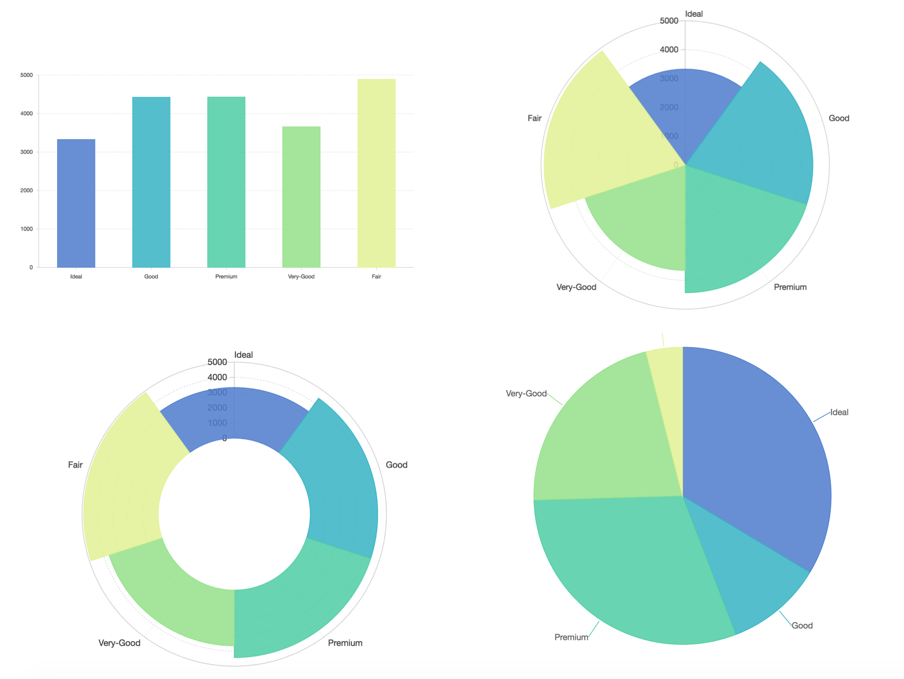
坐标系和图形
可视化编码的两个核心组成部分:几何标记和视觉通道。视觉通道我们已经在前面的章节中介绍过,几何标记我们将在后面的章节中介绍。我们以直角坐标系下的柱状图为例,讲解几何标记在直角坐标系和极坐标系下的不同视觉效果。
直角坐标系
柱状图在直角坐标系下,由四个点构建成的矩形构成:

- 在直角坐标系下,柱状图一般使用x轴方向映射数据的分类,y轴方向映射数据的大小。
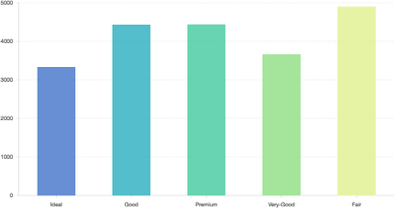
极坐标系
柱状图到了极坐标下,依然由四个点连接而成,变化仅仅在于到圆心距离相等的两个点间的直线变成圆弧:
- 在极坐标系下,柱状图就自然而然的转换成为了玫瑰图
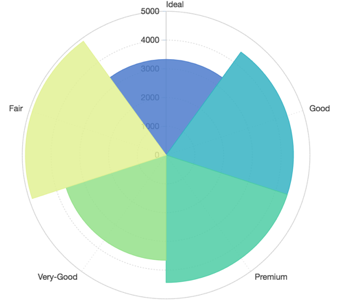
可视化的过程是数据到图形的映射过程,只要数据映射的通道一致,那么我们就可以使用一种方式将几何图形在不同的坐标系下绘制出来。
层叠柱状图到嵌套环图
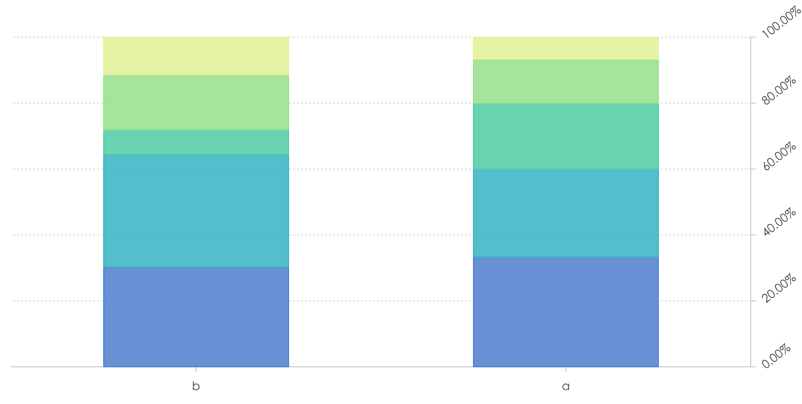
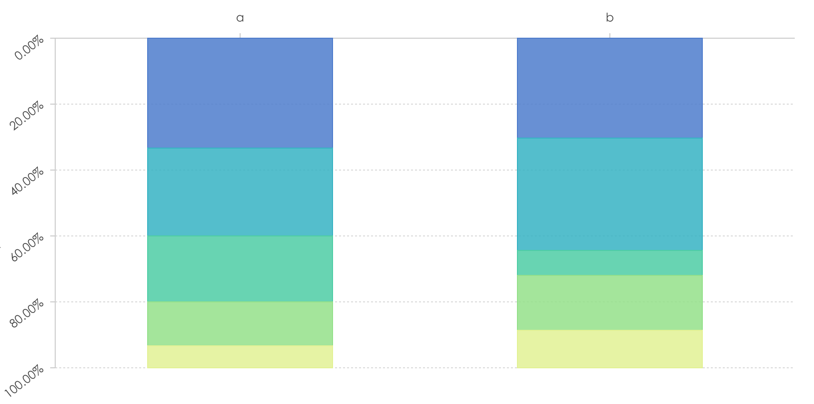
下面的柱状图所有的项累加起来是100%,占用了全部的高度,各项层叠。
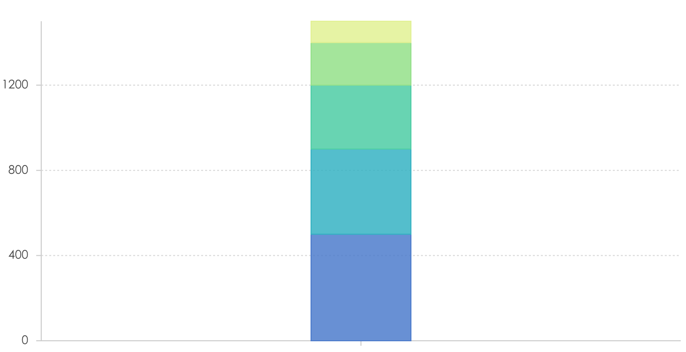
- 分类只有一个,x轴用于区分分类,y轴表示数据的大小
此时我们将坐标系转换成极坐标系:
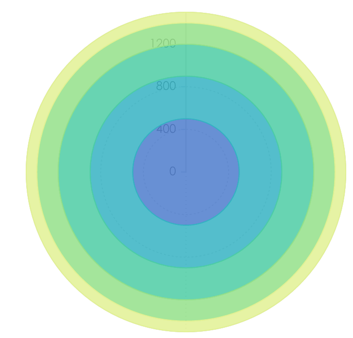
- 由于分类只有一个,所以占有了整个圆环,y轴表示数据的大小
层叠柱状图到饼图
依然是上面的示例,我们将x轴、y轴置换,y轴表示数据的分类,x轴表示数据的大小:
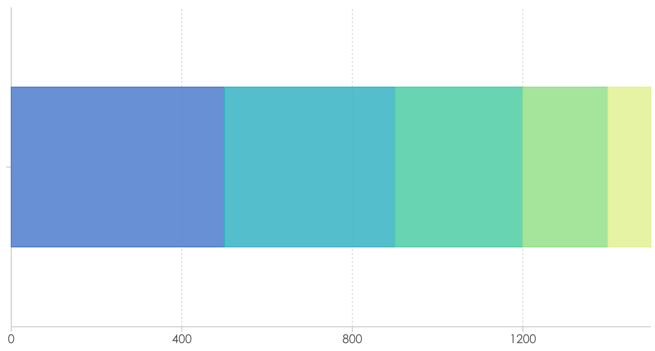
此时我们将坐标系转换成极坐标系:
饼图就生成了,此时如果我们使用两个分类的数据,会出现什么效果?看下图:
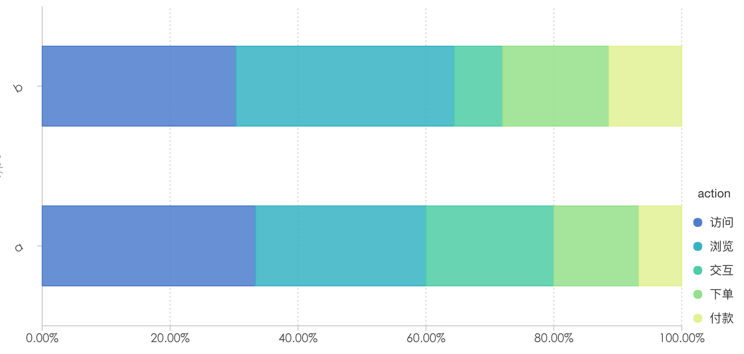
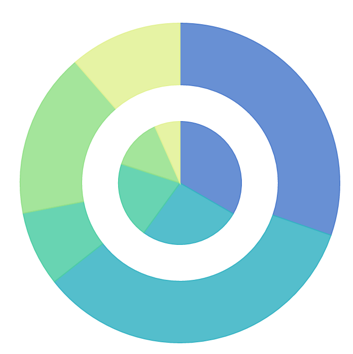
此时就生成了嵌套的饼图
坐标系和视觉通道
上面我们讲解了相同的几何图形在不同坐标系下的不同展示效果,由于直角坐标系是两个垂直向量构建而成的,视觉通道都是位置(postion)的两个子通道(x,y),而极坐标,是由角度和长度两个维度构建而成,角度和位置在视觉通道中的表现力有所差异:
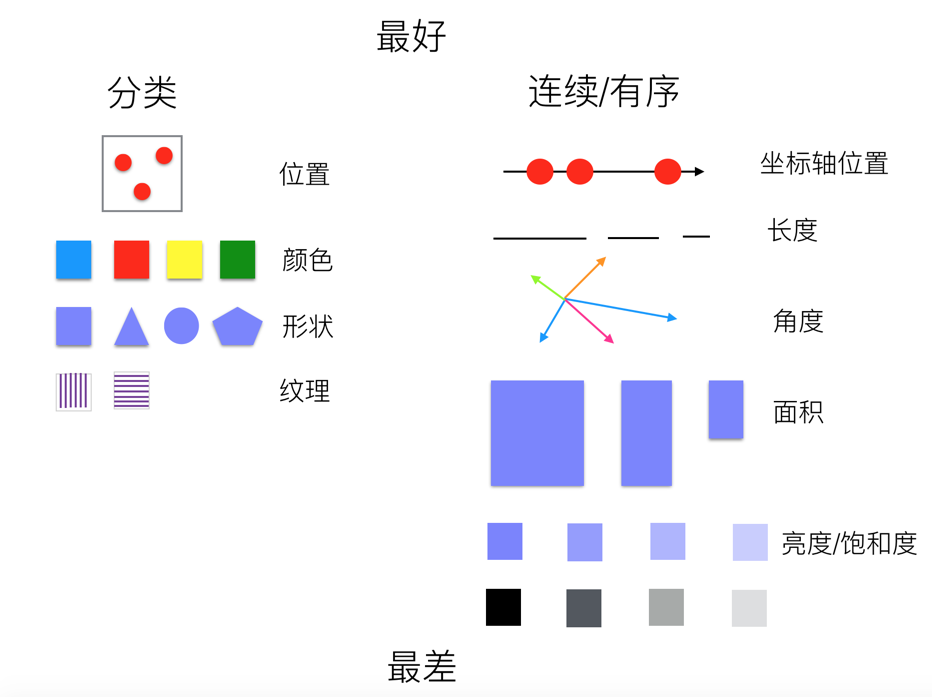
所以在使用图形和坐标系时需要理解清晰数据字段和视觉通道的映射关系,在合适的场景选择合适的视觉通道。
坐标系的转置
坐标系可以进行以下操作:
- translate: 平移,沿x,y轴方向移动
- rotate: 旋转,默认按照坐标系中心旋转
- scale: 放大、缩小,默认按照坐标系中心放大、缩小
-
transpose: x,y轴交换,例如柱状图转换成水平柱状图(条形图)
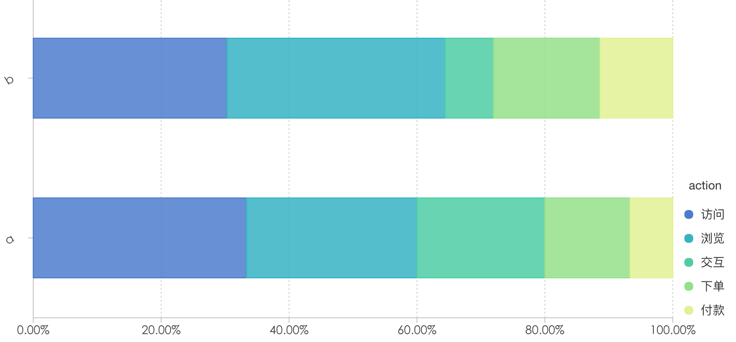
-
reflect: 镜像, 沿x方向镜像或者沿y轴方向映射
- x轴方向镜像
- y轴方向镜像
坐标系的接口设计
结合上面的内容,直角坐标系和极坐标系必须具有的属性或接口:
-
在画布上的范围,需要指定起始点、结束点
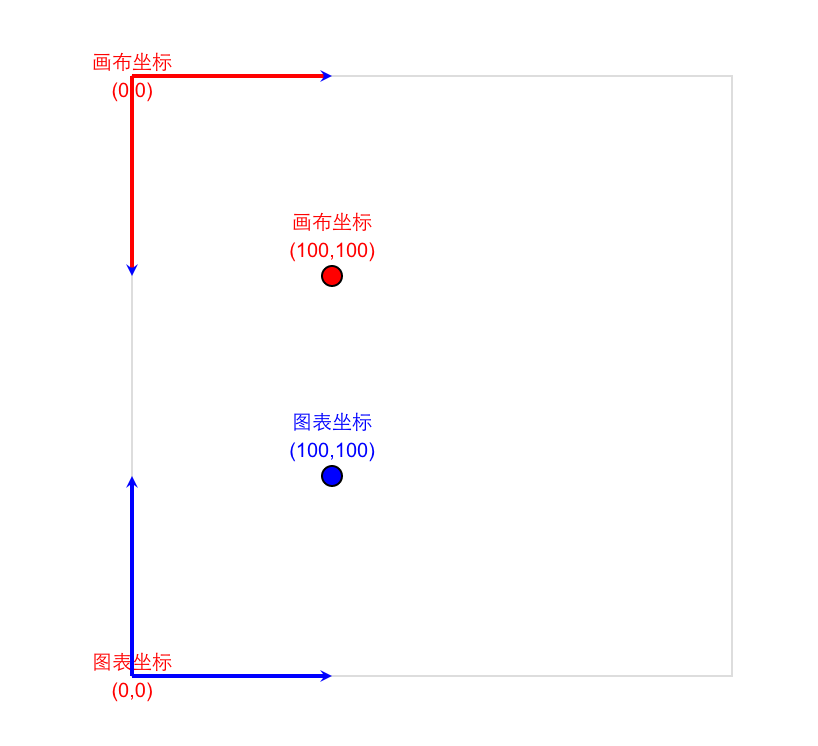
-
将数据从0-1映射到画布坐标,将画布上的坐标反转回数据0-1的范围内
- 坐标系的平移、旋转、放大缩小、镜像等转置功能
属性
| 属性名 | 含义 |
|---|---|
| start | 坐标系的起始点 |
| end | 坐标系的结束点 |
方法
| 方法名 | 含义 |
|---|---|
| convert(point) | 将数据从0-1空间映射到画布空间 |
| invert(point) | 将数据从画布空间反转回0-1空间 |
| translate(x,y) | 平移 |
| rotate(angle) | 旋转 |
| scale(sx,sy) | 方法、缩小 |
| transpose() | x,y交换 |
| reflect(‘x’ | ‘y’) |
极坐标的特殊属性
由于极坐标是由角度和半径长度两个维度共同构成的,所以有自己特有的属性:
| 方法名 | 含义 |
|---|---|
| radius | 半径长度,0-1范围内的数值,最终的半径长度 = min(长,宽) / 2 * radius |
| inner | plus坐标系下,内部空白的半径大小,空白的半径 = min(长,宽) / 2 * inner |
| startAngle | 极坐标的起始角度 |
| endAngle | 极坐标的结束角度 |
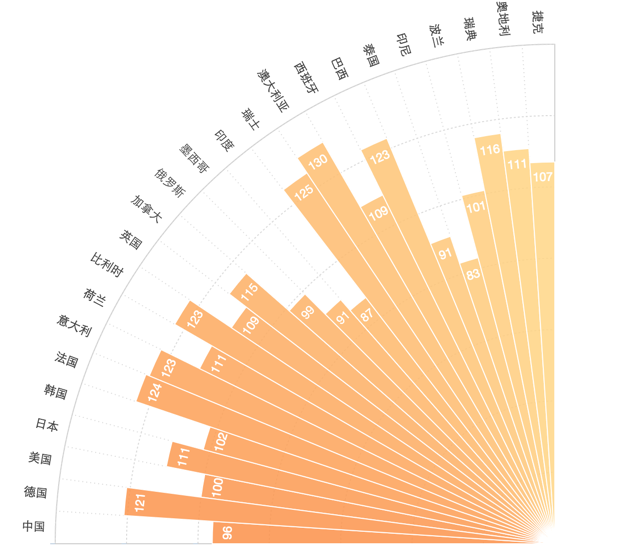
指定了起始角度、结束角度的玫瑰图:
更多
本章介绍了常见的坐标系及其功能,同时介绍了G2如何设计坐标系,在G2中坐标系和几何标记是完全正交的可以自由搭配,后面的章节里面会有更多的体现。下一章节开始几何标记的介绍