A. FashionabLEE
网址:https://codeforces.com/problemset/problem/1369/A
Lee is going to fashionably decorate his house for a party, using some regular convex polygons...
Lee thinks a regular n-sided (convex) polygon is beautiful if and only if he can rotate it in such a way that at least one of its edges is parallel to the OX-axis and at least one of its edges is parallel to the OY-axis at the same time.
Recall that a regular n-sided polygon is a convex polygon with n vertices such that all the edges and angles are equal.
Now he is shopping: the market has t regular polygons. For each of them print YES if it is beautiful and NO otherwise.
Input
The first line contains a single integer t ((1≤t≤10^4)) — the number of polygons in the market.
Each of the next t lines contains a single integer (n_i) ((3 ≤ n_i ≤ 10^9)): it means that the i-th polygon is a regular (n_i)-sided polygon.
Output
For each polygon, print YES if it's beautiful or NO otherwise (case insensitive).
Example
input
4
3
4
12
1000000000
output
NO
YES
YES
YES
Note
In the example, there are 4 polygons in the market. It's easy to see that an equilateral triangle (a regular 3-sided polygon) is not beautiful, a square (a regular 4-sided polygon) is beautiful and a regular 12-sided polygon (is shown below) is beautiful as well.
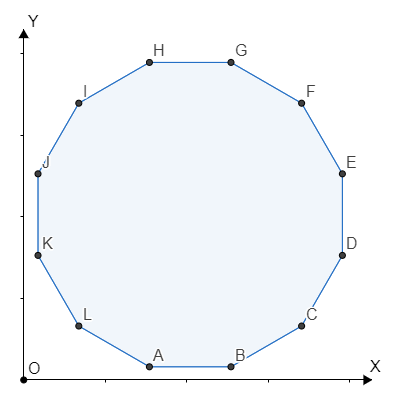
啥都不用说了。
代码如下:
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
int T;
scanf("%d", &T);
while(T --)
{
int n;
scanf("%d", &n);
if(n % 4) puts("NO");
else puts("YES");
}
return 0;
}
B. AccurateLee
网址:https://codeforces.com/problemset/problem/1369/B
Lee was cleaning his house for the party when he found a messy string under the carpets. Now he'd like to make it clean accurately and in a stylish way...
The string s he found is a binary string of length n (i. e. string consists only of 0-s and 1-s).
In one move he can choose two consecutive characters si and si+1, and if si is 1 and si+1 is 0, he can erase exactly one of them (he can choose which one to erase but he can't erase both characters simultaneously). The string shrinks after erasing.
Lee can make an arbitrary number of moves (possibly zero) and he'd like to make the string s as clean as possible. He thinks for two different strings x and y, the shorter string is cleaner, and if they are the same length, then the lexicographically smaller string is cleaner.
Now you should answer t test cases: for the i-th test case, print the cleanest possible string that Lee can get by doing some number of moves.
Small reminder: if we have two strings x and y of the same length then x is lexicographically smaller than y if there is a position i such that x1=y1, x2=y2,..., xi−1=yi−1 and xi<yi.
Input
The first line contains the integer t ((1≤t≤10^4)) — the number of test cases.
Next 2t lines contain test cases — one per two lines.
The first line of each test case contains the integer n ((1≤n≤10^5)) — the length of the string s.
The second line contains the binary string s. The string s is a string of length n which consists only of zeroes and ones.
It's guaranteed that sum of n over test cases doesn't exceed (10^5).
Output
Print t answers — one per test case.
The answer to the i-th test case is the cleanest string Lee can get after doing some number of moves (possibly zero).
Example
input
5
10
0001111111
4
0101
8
11001101
10
1110000000
1
1
output
0001111111
001
01
0
1
Note
In the first test case, Lee can't perform any moves.
In the second test case, Lee should erase s2.
In the third test case, Lee can make moves, for example, in the following order: 11001101 → 1100101 → 110101 → 10101 → 1101 → 101 → 01.
这道题我用数据结构(栈)模拟了整个过程,其实可以更优秀。
考虑:如果1在该序列最右边,那么这些1是消不掉;如果0在该序列最左边,那么同理,这些0怎么消也消不掉。
对于中间的那一子段,一定可以消只剩下一个数字,0或1。显然0更优。
两种代码(我的和standard)如下:
#include<iostream>
#include<cstdio>
#include<stack>
using namespace std;
const int maxn = 100000 + 15;
int n, a[maxn];
int main()
{
int T;
stack <int> s;
scanf("%d", &T);
while(T --)
{
while(!s.empty()) s.pop();
scanf("%d", &n);
for(int i = 1; i <= n; ++ i) scanf("%1d", &a[i]);
for(int i = n; i; -- i)
{
if(s.empty() || s.top() == 1)
{
s.push(a[i]);
continue;
}
if(a[i] == 0) s.push(a[i]);
else
{
while(!s.empty() && !s.top())
{
s.pop();
}
s.push(a[i] - 1);
}
}
while(!s.empty())
{
printf("%d", s.top());
s.pop();
}
puts("");
}
return 0;
}
/*
version of std:
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const int maxn = 100000 + 5;
int n, s[maxn];
int main()
{
int T;
scanf("%d", &T);
while(T --)
{
scanf("%d", &n);
for(int i = 0; i < n; ++ i) scanf("%1d", &s[i]);
int l = 0, r = 0;
for(int i = 0; i < n; ++ i)
{
if(s[i] == 1) break;
++ l;
}
for(int i = n - 1; i >= 0; -- i)
{
if(s[i] == 0) break;
++ r;
}
if(l + r == n)
{
for(int i = 0; i < l; ++ i) putchar('0');
for(int i = 0; i < r; ++ i) putchar('1');
}
else
{
for(int i = 0; i < l; ++ i) putchar('0');
putchar('0');
for(int i = 0; i < r; ++ i) putchar('1');
}
puts("");
}
return 0;
}
*/
C. RationalLee
网址:https://codeforces.com/problemset/problem/1369/C
Lee just became Master in Codeforces, and so, he went out to buy some gifts for his friends. He bought n integers, now it's time to distribute them between his friends rationally...
Lee has n integers a1,a2,…,an in his backpack and he has k friends. Lee would like to distribute all integers in his backpack between his friends, such that the i-th friend will get exactly wi integers and each integer will be handed over to exactly one friend.
Let's define the happiness of a friend as the sum of the maximum and the minimum integer he'll get.
Lee would like to make his friends as happy as possible, in other words, he'd like to maximize the sum of friends' happiness. Now he asks you to calculate the maximum sum of friends' happiness.
Input
The first line contains one integer t ((1 ≤ t ≤ 10^4)) — the number of test cases.
Next 3t lines contain test cases — one per three lines.
The first line of each test case contains two integers n and k ((1 ≤ n ≤ 2⋅10^5; 1 ≤ k ≤ n)) — the number of integers Lee has and the number of Lee's friends.
The second line of each test case contains n integers a1,a2,…,an ((−10^9 ≤ ai ≤ 10^9)) — the integers Lee has.
The third line contains k integers w1,w2,…,wk ((1≤wi≤n; w1 + w2 + … + wk=n)) — the number of integers Lee wants to give to each friend.
It's guaranteed that the sum of n over test cases is less than or equal to (2⋅10^5).
Output
For each test case, print a single integer — the maximum sum of happiness Lee can achieve.
Example
input
3
4 2
1 13 7 17
1 3
6 2
10 10 10 10 11 11
3 3
4 4
1000000000 1000000000 1000000000 1000000000
1 1 1 1
output
48
42
8000000000
Note
In the first test case, Lee should give the greatest integer to the first friend (his happiness will be (17+17)) and remaining integers to the second friend (his happiness will be (13+1)).
In the second test case, Lee should give ({10,10,11}) to the first friend and to the second friend, so the total happiness will be equal to ((11+10)+(11+10))
In the third test case, Lee has four friends and four integers, it doesn't matter how he distributes the integers between his friends.
先考虑最大值。显然,最大值顺次分配即可。这时候,我们先将每个人的分配个数按从小到大的顺序排序,优先满足少的。
对于最小值,只分配一个的人最大值等于最小值,因此我们可以不必考虑了。其他的,利用贪心问题得解。
过程真的很复杂,但很妙,
具体证明见Tutorial:https://codeforces.com/blog/entry/79235
代码如下:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const int SIZE = 2000000;
long long n, a[SIZE], k, w[SIZE];
int main()
{
int t;
scanf("%d", &t);
while(t --)
{
scanf("%d %d", &n, &k);
for(int i = 0; i < n; ++ i) scanf("%lld", &a[i]);
sort(a, a + n);
for(int i = 0; i < k; ++ i)
{
scanf("%lld", &w[i]);
}
sort(w, w + k);
int l = n, head = 0;
long long ans = 0;
for(int i = 0; i < k; ++ i)
{
-- l;
if(w[i] > 1) ans += a[l];
else
{
ans += a[l] * 2;
head = i + 1;
}
}
for(int i = 0; i < k; ++ i) -- w[i];
for(int i = head; i < k; ++ i)
{
l -= w[i];
ans += a[l];
}
printf("%lld
", ans);
}
return 0;
}
D. TediousLee
网址:https://codeforces.com/problemset/problem/1369/D
Lee tried so hard to make a good div.2 D problem to balance his recent contest, but it still doesn't feel good at all. Lee invented it so tediously slow that he managed to develop a phobia about div.2 D problem setting instead. And now he is hiding behind the bushes...
Let's define a Rooted Dead Bush (RDB) of level n as a rooted tree constructed as described below.
A rooted dead bush of level 1 is a single vertex. To construct an RDB of level i we, at first, construct an RDB of level i−1, then for each vertex u:
- if u has no children then we will add a single child to it;
- if u has one child then we will add two children to it;
- if u has more than one child, then we will skip it.
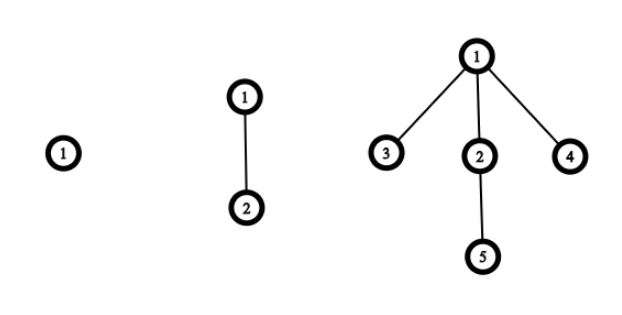
Rooted Dead Bushes of level 1, 2 and 3.
Let's define a claw as a rooted tree with four vertices: one root vertex (called also as center) with three children. It looks like a claw:

The center of the claw is the vertex with label 1.
Lee has a Rooted Dead Bush of level n. Initially, all vertices of his RDB are green.
In one move, he can choose a claw in his RDB, if all vertices in the claw are green and all vertices of the claw are children of its center, then he colors the claw's vertices in yellow.
He'd like to know the maximum number of yellow vertices he can achieve. Since the answer might be very large, print it modulo (10^9+7).
Input
The first line contains one integer t ((1≤t≤10^4)) — the number of test cases.
Next t lines contain test cases — one per line.
The first line of each test case contains one integer n ((1≤n≤2⋅10^6)) — the level of Lee's RDB.
Output
For each test case, print a single integer — the maximum number of yellow vertices Lee can make modulo (10^9+7).
Example
input
7
1
2
3
4
5
100
2000000
output
0
0
4
4
12
990998587
804665184
Note
It's easy to see that the answer for RDB of level 1 or 2 is 0.
The answer for RDB of level 3 is 4 since there is only one claw we can choose: ({1,2,3,4}).
The answer for RDB of level 4 is 4 since we can choose either single claw ({1,3,2,4}) or single claw ({2,7,5,6}). There are no other claws in the RDB of level 4 (for example, we can't choose ({2,1,7,6}), since 1 is not a child of center vertex 2).
Rooted Dead Bush of level 4.
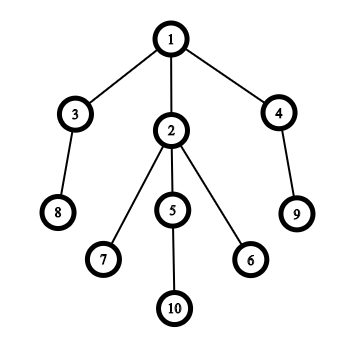
这是我见过最好的一道树形DP题。
首先明确一点:等级i的树是由等级i-1和等级i-2的组成的。
不妨设(dp[i])代表等级i的树最大值为多少。
很显然,如果等级i的根节点不染色,那么它最大值一定来源于三棵子树。于是有:(dp[i] = dp[i - 1] + dp[i - 2] * 2);
如果根节点染色,那么三棵子树的所有根节点一定不能染色。考虑到只有3的倍数符合。由此:(dp[i] = dp[i - 1] + dp[i - 2] * 2 + (i % 3) ? 0 : 4;)
代码如下:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
const int maxn = 2000000 + 1, mod = 1000000007;
int n;
long long dp[maxn] = {};
int main()
{
int T;
scanf("%d", &T);
for(int i = 3; i < maxn; ++ i) dp[i] = (dp[i - 1] + dp[i - 2] * 2 + (!(i % 3) ? 4 : 0)) % mod;
while(T --)
{
scanf("%d", &n);
printf("%d
", dp[n]);
}
return 0;
}