胜败兵家事不期,包羞忍耻是男儿。
江东子弟多才俊,卷土重来未可知。——杜牧
基本的广搜适用于无权图求最短路,若为带权图,那么普通广搜就不能使用了。
于是,我们有以下几种做法:其中,优先队列bfs最常见,可以和估价函数提高效率。
一、双端队列广搜
如果遍历的图的边权为1或0,可以使用双端队列广搜;
具体地,如果该图边权全为1,那么就是普通广度优先;
但如果有权是0的边怎么办?我们认为,在一个边权只为0的联通块中,我们把它缩成一个单独的节点(缩点),因为既然为0,那么这个联通块中任意一个点到其它点的代价为0,不如把它看作一个点,为了方便叙述,称这样的点为”0权“节点;
对于缩点后的情况,我们不难想到,这张图转化成一张无权图。我们只需要对于这张图进行BFS。
可是,缩点不免有些困难,实现起来比较复杂;
那么,可以把普通队列改造成双端队列,其中一个端口起到了缩点找联通块的作用。
我们考虑,当该状态扩展了一条边权为一的边时,将其按照标准操作进行;
反之,我们把新状态压入队列的首项,每次扩展队列的首项状态。
为什么是对的?
我们把边权为0的一条边所指向的结点放入队首,对于整个”0权“节点相当于没有扩展,只是在遍历整个联通块;而对于边权为一的边所指向的状态,放入队列尾,则就是对于该”0权“节点的一次扩展变换。
例题:电路维修
网址:http://noi-test.zzstep.com/contest/0x20「搜索」例题/2601 电路维修
描述
Ha'nyu是来自异世界的魔女,她在漫无目的地四处漂流的时候,遇到了善良的少女Rika,从而被收留在地球上。Rika的家里有一辆飞行车。有一天飞行车的电路板突然出现了故障,导致无法启动。
电路板的整体结构是一个R行C列的网格(R,C≤500),如右图所示。
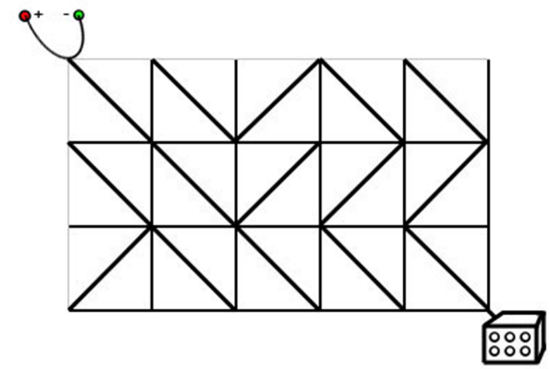
每个格点都是电线的接点,每个格子都包含一个电子元件。电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。在旋转之后,它就可以连接另一条对角线的两个接点。电路板左上角的接点接入直流电源,右下角的接点接入飞行车的发动装置。
Ha'nyu发现因为某些元件的方向不小心发生了改变,电路板可能处于断路的状态。她准备通过计算,旋转最少数量的元件,使电源与发动装置通过若干条短缆相连。不过,电路的规模实在是太大了,Ha'nyu并不擅长编程,希望你能够帮她解决这个问题。
输入格式
输入文件包含多组测试数据。第一行包含一个整数T 表示测试数据的数目。
对于每组测试数据,第一行包含正整数R 和C,表示电路板的行数和列数。
之后R 行,每行C 个字符,字符是"/"和""中的一个,表示标准件的方向。
输出格式
对于每组测试数据,在单独的一行输出一个正整数,表示所需的缩小旋转次数。
如果无论怎样都不能使得电源和发动机之间连通,输出NO SOLUTION。
样例输入
1
3 5
\/\
\///
/\\
样例输出
1
数据范围
对于100% 的数据,R,C≤500,T≤5。
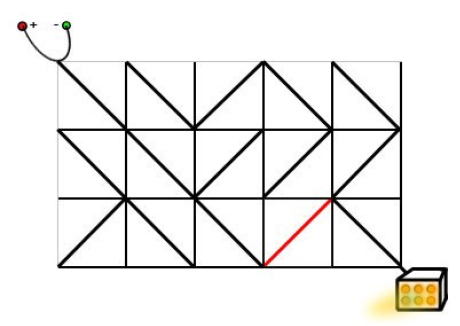
样例解释
样例的输入对应于题目描述中的情况。
只需要按照下面的方式旋转标准件,就可以使得电源和发动机之间连通。
这道题非常玄乎,但不过由于学习双端队列广搜后,不难发现,对于图中的横纵十字交点,可以当做一个节点,起点和终点给定,连边,如果不连这边权为1;否则,边权为0。该图即为我们讨论过的0-1权图。
代码如下:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<deque>
#include<cmath>
#define pii pair <int , int>
#define y second
#define x first
using namespace std;
const int MAX_size = 500 + 5;
struct edge
{
pii to;
int next, w;
} e[MAX_size * MAX_size * 4];
bool book[MAX_size][MAX_size];
int R, C, tot = 0, head[MAX_size][MAX_size] = {};
int d[MAX_size][MAX_size] = {};
deque <pii> Q;
char g[MAX_size];
void add_edge(pii x, pii y, int z) {
e[++ tot].to = y;
e[tot].w = z;
e[tot].next = head[x.x][x.y];
head[x.x][x.y] = tot;
return;
}
void init() {
tot = 0;
memset(book, false, sizeof(book));
memset(head, 0, sizeof(head));
memset(d, 0x3f, sizeof(d));
return;
}
int bfs() {
Q.clear();
Q.push_back(make_pair(0, 0));
d[0][0] = 0;
while(!Q.empty())
{
pii now = Q.front();
Q.pop_front();
if(book[now.x][now.y]) continue;
book[now.x][now.y] = true;
if(now == make_pair(R, C)) return d[now.x][now.y];
for(int i = head[now.x][now.y]; i; i = e[i].next)
{
pii v = e[i].to;
d[v.x][v.y] = min(d[v.x][v.y], d[now.x][now.y] + e[i].w);
if(!e[i].w) Q.push_front(v);
else Q.push_back(v);
}
}
if(d[R][C] < 0x3f) return d[R][C];
return -1;
}
int main()
{
int T;
scanf("%d", &T);
while(T --)
{
scanf("%d %d", &R, &C);
init();
for(int i = 1; i <= R; ++ i) {
scanf("%s", g + 1);
for(int j = 1; j <= C; ++ j) {//连边,将矩形转化为图,将十字交点转化为图中结点。
pii x1 = make_pair(i - 1, j - 1), y1 = make_pair(i, j);
pii x2 = make_pair(i, j - 1), y2 = make_pair(i - 1, j);
if(g[j] == '\') {
add_edge(x1, y1, 0);
add_edge(y1, x1, 0);
add_edge(x2, y2, 1);
add_edge(y2, x2, 1);
}
if(g[j] == '/') {
add_edge(x2, y2, 0);
add_edge(y2, x2, 0);
add_edge(x1, y1, 1);
add_edge(y1, x1, 1);
}
}
}
int ans = bfs();
if(ans != -1) printf("%d
", ans);
else puts("NO SOLUTION");//注意细节!
}
return 0;
}
二、优先队列bfs
如果图中更一般地情况是:边权不止为1或0,那么,将普通队列改成优先队列可以很高效地求解。
如果仍为标准队列,那么,该队列不再满足单调性,只有通过不断更新直到无法更新后(松弛),才停止。经典算法是Bellman-Ford (SPFA) 最短路算法。
采用优先队列BFS要优于上述。对应经典算法为Dijkstra的最短路算法。
例题:装满的油箱
网址:http://poj.org/problem?id=3635
有N个城市(编号0、1…N-1)和M条道路,构成一张无向图。
在每个城市里边都有一个加油站,不同的加油站的单位油价不一样。
现在你需要回答不超过100个问题,在每个问题中,请计算出一架油箱容量为C的车子,从起点城市S开到终点城市E至少要花多少油钱?
注意: 假定车子初始时油箱是空的。
输入格式
第一行包含两个整数N和M。
第二行包含N个整数,代表N个城市的单位油价,第i个数即为第i个城市的油价pi。
接下来M行,每行包括三个整数u,v,d,表示城市u与城市v之间存在道路,且车子从u到v需要消耗的油量为d。
接下来一行包含一个整数q,代表问题数量。
接下来q行,每行包含三个整数C、S、E,分别表示车子油箱容量、起点城市S、终点城市E。
输出格式
对于每个问题,输出一个整数,表示所需的最少油钱。
如果无法从起点城市开到终点城市,则输出”impossible”。
每个结果占一行。
数据范围
1≤N≤1000,1≤M≤10000;
1≤pi≤100,1≤d≤100,1≤C≤100;
输入样例:
5 5
10 10 20 12 13
0 1 9
0 2 8
1 2 1
1 3 11
2 3 7
2
10 0 3
20 1 4
输出样例:
170
impossible
如果没有油箱的设置,那么这道题就是直接的最短路问题。
如果有油箱,那么,考虑状态(now,fuel)代表在第now个城市油箱剩余fuel
如果该边可以通过,就更新入队列;否则,就将(now,fuel + 1)入队,并更新相应的代价。
代码如下:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
#include<cmath>
#define maxn 20000 + 5
#define maxm 100 + 10
using namespace std;
struct node
{
int cost, city, fuel;
node(int x, int y, int z): cost(x), city(y), fuel(z)
{}
bool operator < (const node& rhs) const
{
return cost > rhs.cost;
}
};
struct edge
{
int to, next, w;
} e[maxn];
bool vis[maxn][maxm];
int n, m, tot = 0, head[maxn], p[maxn] = {}, d[maxn][maxm] = {};
void add_edge(int x, int y, int z)
{
e[++ tot].to = y;
e[tot].w = z;
e[tot].next = head[x];
head[x] = tot;
return;
}
int bfs(int C, int S, int E)
{
priority_queue <node> Q;
while(!Q.empty()) Q.pop();
memset(vis, false, sizeof(vis));
memset(d, 0x3f, sizeof(d));
d[S][0] = 0;
Q.push(node(0, S, 0));
while(!Q.empty())
{
node now = Q.top();
int u = now.city, f = now.fuel;
Q.pop();
if(vis[u][f]) continue;
if(u == E) return d[u][f];
vis[u][f] = true;
if(f < C)
{
if(d[u][f + 1] > d[u][f] + p[u])
{
d[u][f + 1] = d[u][f] + p[u];
Q.push(node(d[u][f + 1], u, f + 1));
}
}
for(int i = head[u]; i; i = e[i].next)
{
int v = e[i].to, w = e[i].w;
if(w > f) continue;
if(d[v][f - w] > d[u][f])
{
d[v][f - w] = d[u][f];
Q.push(node(d[v][f - w], v, f - w));
}
}
}
return -1;
}
int main()
{
int q;
scanf("%d %d", &n, &m);
for(int i = 0; i < n; ++ i) scanf("%d", &p[i]);
int x, y, z;
for(int i = 0; i < m; ++ i)
{
scanf("%d %d %d", &x, &y, &z);
add_edge(x, y, z);
add_edge(y, x, z);
}
scanf("%d", &q);
int C, S, E;
int ans;
for(int t = 1; t <= q; ++ t)
{
ans = 0;
scanf("%d %d %d", &C, &S, &E);
ans = bfs(C, S, E);
if(ans != -1) printf("%d
", ans);
else
{
puts("impossible");
}
}
return 0;
}
要注意细节!!
三、双向广搜
对于一颗搜索树,规模巨大,换句话来讲,分支很多,并且层数很深,那么,我们可以采取双向BFS。
若该题状态空间允许使用广搜(bfs),那么双向广搜表现将非常优秀:
不妨设搜索树有k层,每层每个分支均可以扩展n个,那么,使用普通的广度搜索时间复杂度将高达
O(n^k)
,而双向广搜则为
O(2*n^{k/2})
。
- 双向广搜的本质其实是从目标状态和初状态每轮各自扩展,从而减小搜索深度和搜索树规模。
- 原理与双向搜索相差不大。
- 与“中途相遇法”异曲同工之妙。
例题:噩梦
HDOJ3085
网址:http://acm.hdu.edu.cn/showproblem.php?pid=3085
给定一张N*M的地图,地图中有1个男孩,1个女孩和2个鬼。
字符“.”表示道路,字符“X”表示墙,字符“M”表示男孩的位置,字符“G”表示女孩的位置,字符“Z”表示鬼的位置。
男孩每秒可以移动3个单位距离,女孩每秒可以移动1个单位距离,男孩和女孩只能朝上下左右四个方向移动。
每个鬼占据的区域每秒可以向四周扩张2个单位距离,并且无视墙的阻挡,也就是在第k秒后所有与鬼的曼哈顿距离不超过2k的位置都会被鬼占领。
注意: 每一秒鬼会先扩展,扩展完毕后男孩和女孩才可以移动。
求在不进入鬼的占领区的前提下,男孩和女孩能否会合,若能会合,求出最短会合时间。
输入格式
第一行包含整数T,表示共有T组测试用例。
每组测试用例第一行包含两个整数N和M,表示地图的尺寸。
接下来N行每行M个字符,用来描绘整张地图的状况。(注意:地图中一定有且仅有1个男孩,1个女孩和2个鬼)
输出格式
每个测试用例输出一个整数S,表示最短会合时间。
如果无法会合则输出-1。
每个结果占一行。
数据范围
1<n,m<800
输入样例:
3
5 6
XXXXXX
XZ..ZX
XXXXXX
M.G...
......
5 6
XXXXXX
XZZ..X
XXXXXX
M.....
..G...
10 10
..........
..X.......
..M.X...X.
X.........
.X..X.X.X.
.........X
..XX....X.
X....G...X
...ZX.X...
...Z..X..X
输出样例:
1
1
-1
状态为两个人的各自位置;若将其打包变为一个状态,则共有四个维度,每次需要遍历16 * 16个状态,超时;
考虑:
建立两个队列,每一轮轮流扩展,对于每个位置分别记录可达性;
若出现扩展到的符合题意位置,与此同时对方可以到达的位置,则说明对方一定能够在这里会和;
而队列仍具有单调性,所以直接将该轮数作为答案。
代码如下:
#include<iostream>
#include<cstring>
#include<bitset>
#include<cstdio>
#include<queue>
#include<cmath>
#define x first
#define y second
#define pii pair <int, int>
using namespace std;
const int MAX_size = 804;
const int dx[4] = {-1, 1, 0, 0}, dy[4] = {0, 0, -1, 1};
pii boy, girl;
pii g[2];
char ch[MAX_size][MAX_size];
int n, m;
bitset <MAX_size> v1[MAX_size], v2[MAX_size];
bool valid(int x, int y, int k)//判断
{
if(x < 1 || x > n || y < 1 || y > m || ch[x][y] == 'X') return false;
for(int i = 0; i < 2; ++ i)
if(abs(g[i].x - x) + abs(g[i].y - y) <= k * 2) return false;
return true;
}
int bfs()
{
queue <pii> q1, q2;
while(!q1.empty()) q1.pop();
while(!q2.empty()) q2.pop();
for(int i = 0; i <= n; ++ i)
{
v1[i].reset();
v2[i].reset();
}
v1[boy.x][boy.y] = true;
v2[girl.x][girl.y] = true;
int cnt1, cnt2, time = 0;
q1.push(boy);
q2.push(girl);
pii now;
while(!q1.empty() && !q2.empty())
{
++ time;
cnt2 = q2.size();
for(int i = 0; i < 3; ++ i)
{
cnt1 = q1.size();
for(int t = 0; t < cnt1; ++ t)
{
now = q1.front();
q1.pop();
if(!valid(now.x, now.y, time)) continue;//鬼先扩展要注意
pii next;
for(int k = 0; k < 4; ++ k)
{
next = make_pair(now.x + dx[k], now.y + dy[k]);
if(!valid(next.x, next.y, time)) continue;
if(v2[next.x][next.y]) return time;
if(!v1[next.x][next.y])
{
q1.push(next);
v1[next.x][next.y] = true;
}
}
}
}
for(int i = 0; i < cnt2; ++ i)
{
now = q2.front();
q2.pop();
if(!valid(now.x, now.y, time)) continue;
pii next;
for(int k = 0; k < 4; ++ k)
{
next = make_pair(now.x + dx[k], now.y + dy[k]);
if(!valid(next.x, next.y, time)) continue;
if(v1[next.x][next.y]) return time;
if(!v2[next.x][next.y])
{
q2.push(next);
v2[next.x][next.y] = true;
}
}
}
}
return -1;
}
int main()
{
int T, cnt = 0;
scanf("%d", &T);
while(T --)
{
scanf("%d %d", &n, &m);
for(int i = 1; i <= n; ++ i)
{
scanf("%s", ch[i] + 1);
for(int j = 1; j <= m; ++ j)
{//记录两人及俩鬼的位置
if(ch[i][j] == 'M') boy = make_pair(i, j);
else if(ch[i][j] == 'G') girl = make_pair(i, j);
else if(ch[i][j] == 'Z') g[cnt ++] = make_pair(i, j);
}
}
printf("%d
", bfs());
cnt = 0;
}
return 0;
}
练习:字串变换 NOIP2002
网址:https://www.luogu.com.cn/problem/P1032
题目描述
已知有两个字串A,B及一组字串变换的规则(至多6个规则):
A1 ->B1
A2 -> B2
规则的含义为:
在 A中的子串 A1 可以变换为B1,A2 可以变换为 B2 …。
例如:A=abcd,B=xyz,
变换规则为:
abc→xu,ud→y,y→yz
则此时,A可以经过一系列的变换变为B,其变换的过程为:
abcd→xud→xy→xyz。
共进行了3次变换,使得A变换为B。
输入格式
输入格式如下:
A B
A1 B1
A2 B2 |-> 变换规则
... ...
所有字符串长度的上限为20。
输出格式
输出至屏幕。格式如下:
若在10步(包含10步)以内能将A变换为B,则输出最少的变换步数;
否则输出"NO ANSWER!"
输入输出样例
输入
abcd xyz
abc xu
ud y
y yz
输出
3
补充说明:对于 string str,str.replace(i,length,s)指的是将字符串str从i开始length个字符全部有序替换为字符串s;
此题最开始如果使用搜索,会发现状态是一个字符串,每次一该字符串扩展,这是一个较难处理的状态,STL 中的 map 可以很好地处理这样的状态。
但是,这样会超时;此时,我们可以双向bfs,大幅度地提升效率;
代码如下:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<string>
#include<cmath>
#include<queue>
#include<map>
using namespace std;
map <string, int> d1, d2;
map <string, bool> v1, v2;
string s, t;
string x[7], y[7];
int cnt = 0;
bool check(string str1, string str2, int p)
{
for(int i = 0; i < str2.size(); ++ i)
if(str1[i + p] != str2[i]) return false;
return true;
}
int bfs()
{
queue <string> q1, q2;
if(s == t) return 0;
while(!q1.empty()) q1.pop();
while(!q2.empty()) q2.pop();
d1.clear(), v1.clear();
d2.clear(), v2.clear();
int pos, i, time;
string p, now, next;
d1[s] = 0, v1[s] = true;
d2[t] = 0, v2[t] = true;
q1.push(s);
q2.push(t);
while(!q1.empty() && !q2.empty())
{
time = q1.size();
while(time --)
{
now = q1.front();
q1.pop();
if(d1[now] > 9) return -1;
p = now;
for(i = 0; i < cnt; ++ i)
{
for(pos = 0; pos < now.size(); ++ pos)
{
if(check(now, x[i], pos))
{
p.replace(pos, x[i].size(), y[i]);
if(!v1[p])
{
d1[p] = d1[now] + 1;
if(v2[p]) return d1[p] + d2[p] > 10 ? -1 : d1[p] + d2[p];
v1[p] = true;
q1.push(p);
}
}
p = now;
}
}
}
time = q2.size();
while(time --)
{
now = q2.front();
q2.pop();
if(d2[now] > 9) return -1;
p = now;
for(i = 0; i < cnt; ++ i)
{
for(pos = 0; pos < now.size(); ++ pos)
{
if(check(now, y[i], pos))
{
p.replace(pos, y[i].size(), x[i]);
if(!v2[p])
{
d2[p] = d2[now] + 1;
if(v1[p]) return d1[p] + d2[p] > 10 ? -1 : d1[p] + d2[p];
v2[p] = true;
q2.push(p);
}
}
p = now;
}
}
}
}
return -1;
}
int main()
{
int ans;
cin >> s >> t;
while(cin >> x[cnt] >> y[cnt]) ++ cnt;
ans = bfs();
if(ans == -1) puts("NO ANSWER!");
else printf("%d
", ans);
return 0;
}