学习资料：
https://www.bilibili.com/video/BV1iW411d7hd （字幕）
https://www.bilibili.com/video/BV1a54y1k7YE （无字幕）
深入理解计算机系统书籍pdf : 链接: https://pan.baidu.com/s/1zWGfoxn0os0s9B3A2joM0Q 提取码: t4uc
豆瓣9.5分的书籍，这是一本"入门"级别的书，覆盖面很广，从计算机的基本组成，二进制数据表示方式，到机器级别的指令，CPU工作方式，存储结构和优化，操作系统的虚拟内存管理，程序运行方式，I/O，网络、到程序性能优化和并行程序开发等，实验部分设计的也很精彩。 本视频对应于该书第3版，是原作者Randal E.Bryant的授课内容。 课件下载: https://pan.baidu.com/s/1ZKz5kYs4c1aWdmosEOx0bw 提取码：ru0t
Lecture01 Bits,Bytes,Integers：
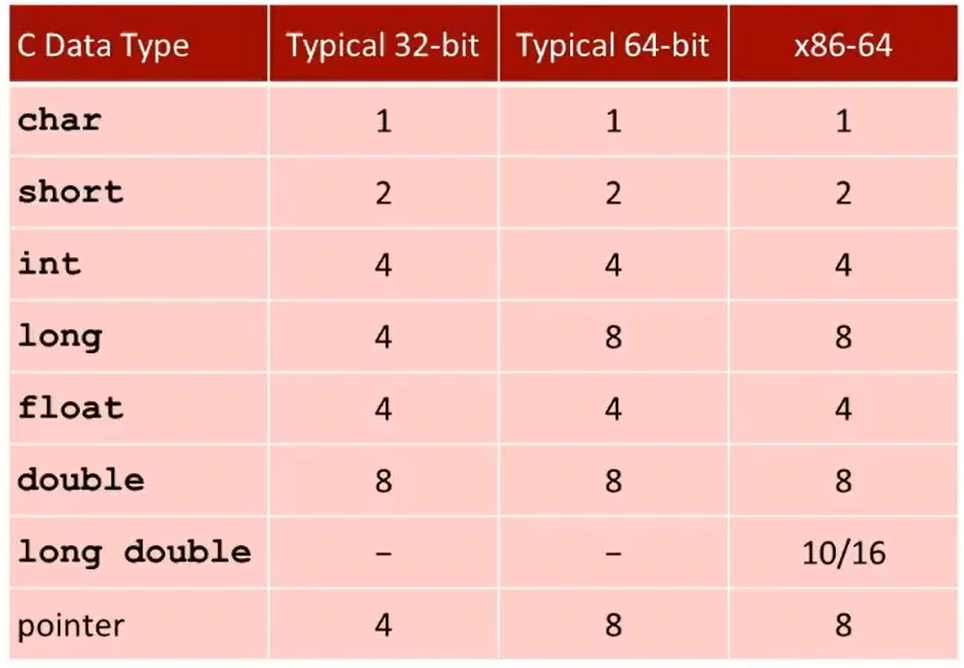
这个课程涉及的都是x86-64位机器
位运算：
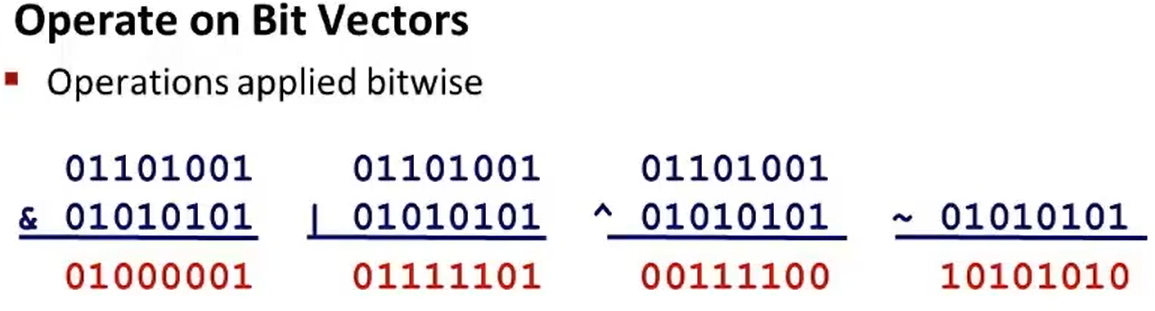
一个应用（表示集合）：
位移操作：
左移的时候，只是用0填充，
右移分为 逻辑右移和算术右移，其中的算术右移填充是用最高位进行填充的！
有符号整数：
例：
这里假定w=4（4位）,
机器中能表示的所有情况：
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 总共有16中表示方法，
第一种方法（补码）：B2T（现代计算机都是使用这种编码方式表示有符号整数）
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
0 1 2 3 4 5 6 7 -8 -7 -6 -5 -4 -3 -2 -1
第二种方法（反码）：B2O
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
+0 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 -0
第三种方法（原码）：B2S
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
+0 1 2 3 4 5 6 7 -0 -1 -2 -3 -4 -5 -6 -7
参考： https://www.cnblogs.com/zach0812/p/11422697.html
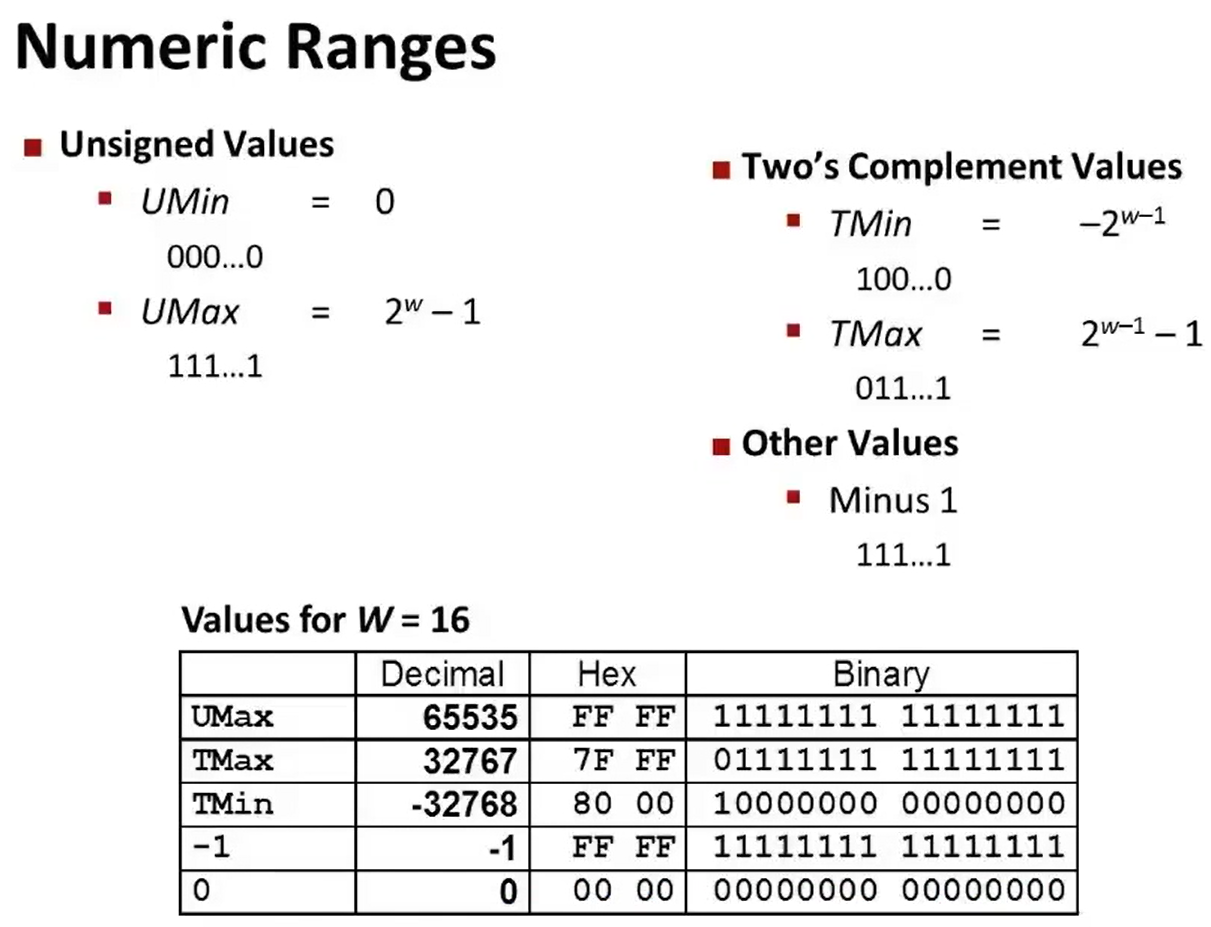
有符号数的扩展，在不改变值的情况下扩展比特：
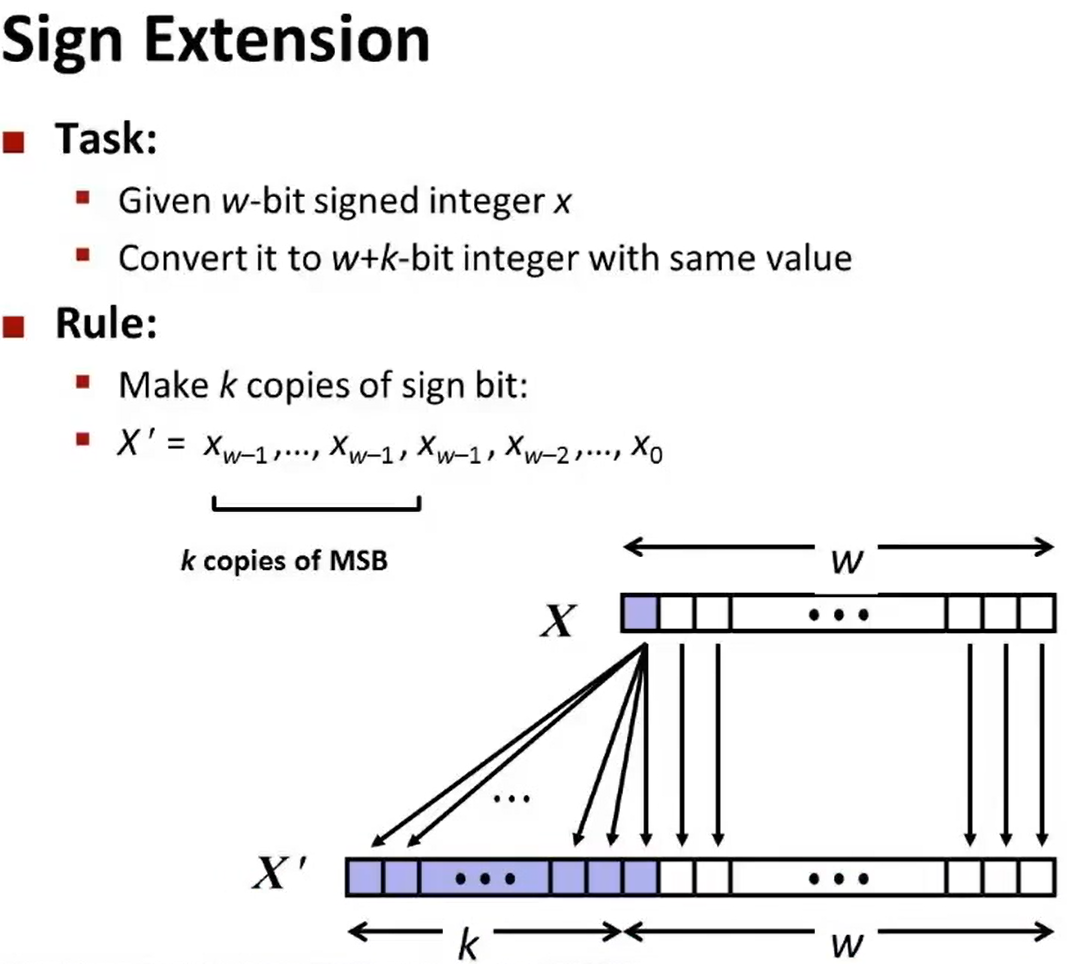
基本的规则是：将符号位复制到左侧来完成，
例如：
0110 -> 0 0110 ，它都是代表6
1110 -> 1 1110 , 它都是代表-2
截断
加法：
例如： w=4 ,
1101 + 0101 = 1 0010
13 5 18%16 = 2
乘法：
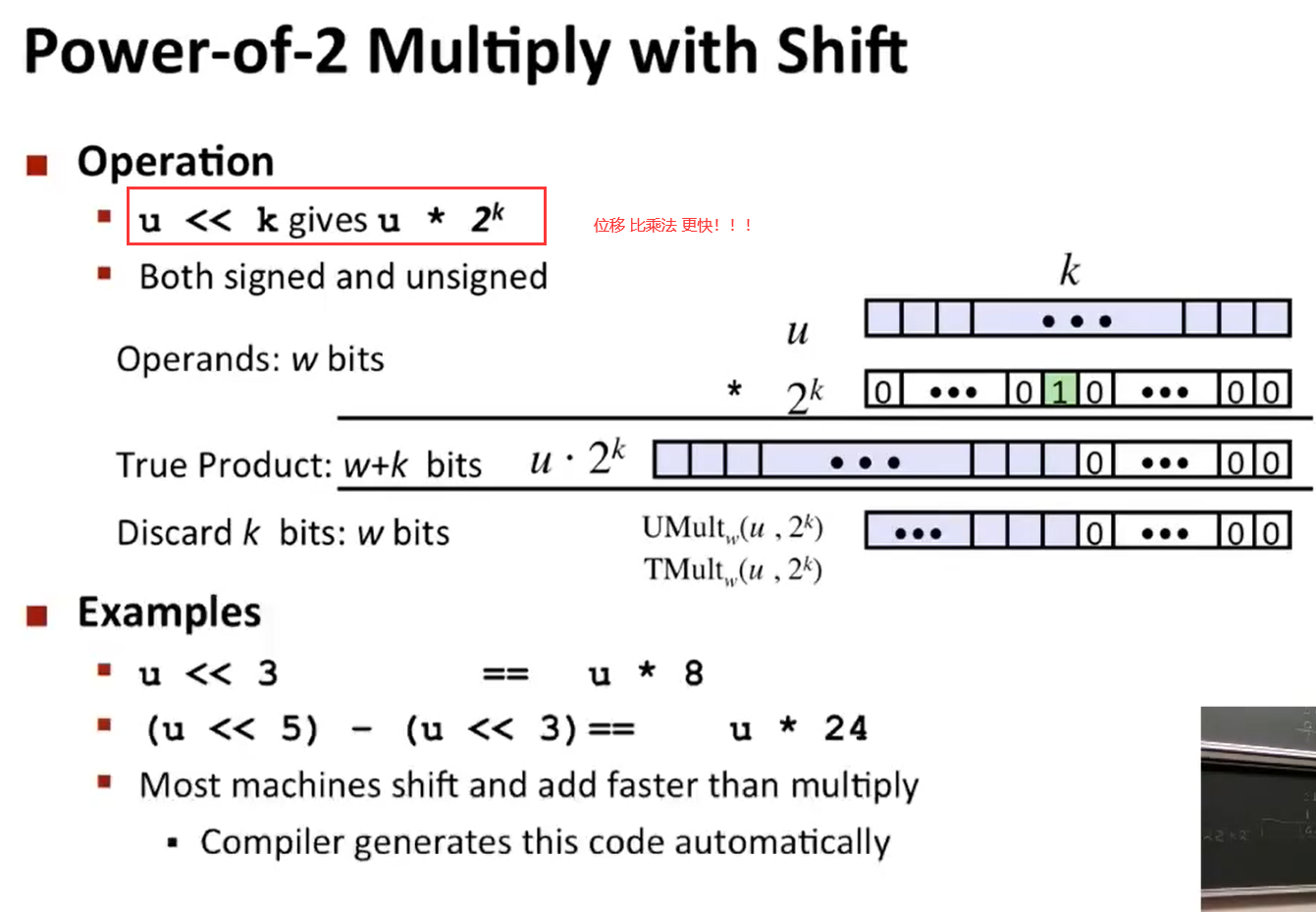
除法的右移
求相反数
将所有的比特反转 然后再加1
整数运算总结：
为什么仍要使用无符号整数
无符号整数容易产生的问题：
既然无符号整数和有符号整数这么复杂，那么我们为什么还使用无符号整数，不应该去掉无符号整数吗（Python,Java就只有有符号整数）？
计算机的字长：
Byte Ordering ：
Lecture02 Floating Point：
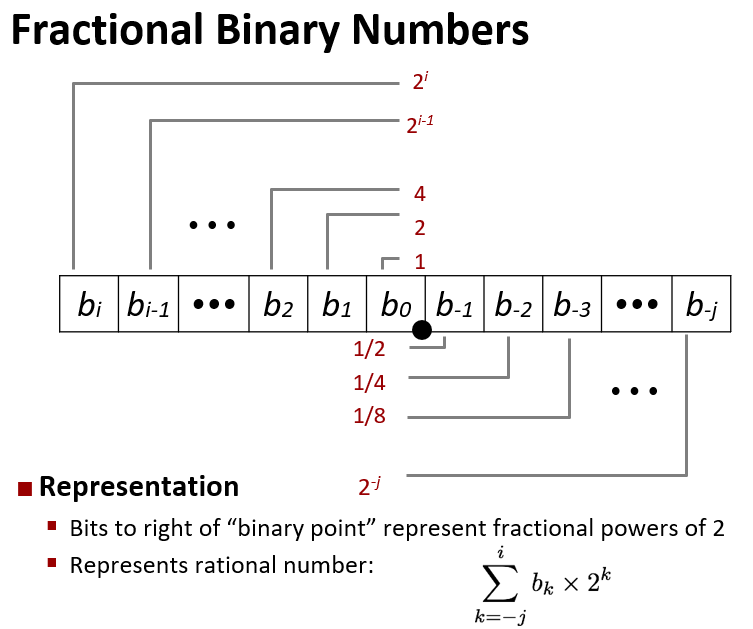
w = 1 -> 8 所能表示的小数：
import matplotlib.pyplot as plt import copy def PowerSetsRecursive(items): # the power set of the empty set has one element, the empty set result = [[]] for x in items: result.extend([subset + [x] for subset in result]) return result input_arrs = [] temp_arr = [] for i in range(1, 9): temp_arr.append(i) input_arrs.append(copy.deepcopy(temp_arr)) w = 1 for input_arr in input_arrs: subsets = PowerSetsRecursive(input_arr) datas = [0, ] # 要绘制的数据 for arr in subsets: if not arr: continue s = 0 for i in arr: s += (1 / 2) ** i datas.append(s) # 对 datas 排序 datas = sorted(datas) # 绘制datas ids = [] # 横坐标 for i in range(len(datas)): ids.append(i) #print(ids) #print(datas) plt.scatter(ids,datas) plt.title(f"w={w}") plt.savefig(f"w={w}") #plt.show() w += 1
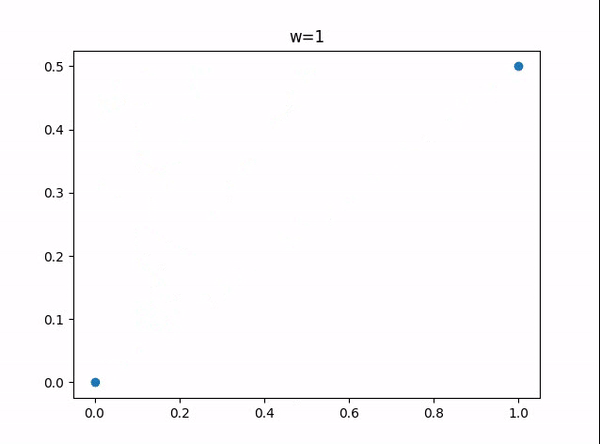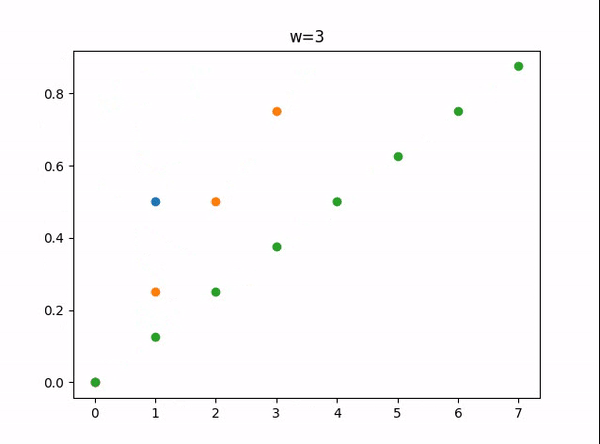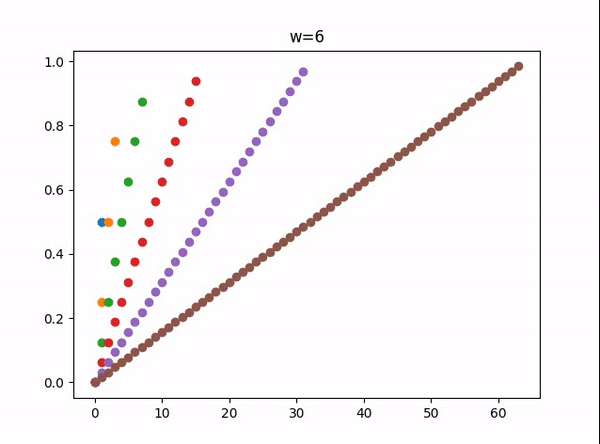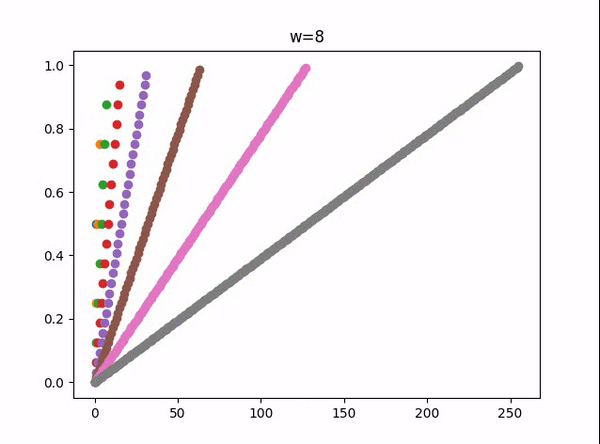
上述表示方法的局限：
它只能表示 形如 ：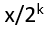 
这样的小数，
其他的小数只能近似的表示，
例如，1/5 的表示，
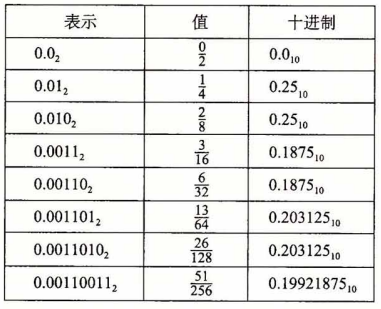
用二进制表示，也有一些是循环的，就像10进制中的1/3 表示为0.3333333 [3]
具体计算过程如下：
IEEE 浮点表示：
IEEE 浮点标准使用如下形式来表示一个数：
Note: Most Significant Bit，在二进制数中属于最高有效位，MSB是最高加权位，与十进制数字中最左边的一位类似。
三种浮点数的格式：（前两种，C中的float 和 C中的double ）
01 Normalized 值：
关于范围：
容易知Exp 域 的范围是 [0,255] 0000 0000 -> 1111 1111
又知，Bias = 127,即 0111 1111
所以，实际的E 的范围是 [-127,128]
总结：
frac域 就是 [1,2) 的小数，具体是 1.xxx...x （2进制），注：1.xxx...x的1 是隐含编码（默认就有了1，就不用再占用一个位置了）！
exp域 是unsigned val ，需要E 额外 加上Bias（偏移），这里可以思考个问题，为什么不用补码来表示exp域？，为了更好的做比较
s 域 是0 或 1
※关于为什么不用补码来表示exp域？
It's just another way of doing negative numbers, instead of two's complement. There's no reason for 0 to actually be represented by zeroes.
There are 8 bits of exponent so 127 gives roughly the same positive and negative range.
02 Denormalized 值：
因为使用第一种normalized values 要求M [1,2) ，所以就无法表示0。所以就有了第二种 Denormalized Values。
它的特征是 exp域全为0 ，它的frac 中没有隐含1， 所以frac 的编码和M完全等价，
为什么要用 Denormalized 来表示接近0的浮点数，用范围 换精度 ！
Special 值：
总结：
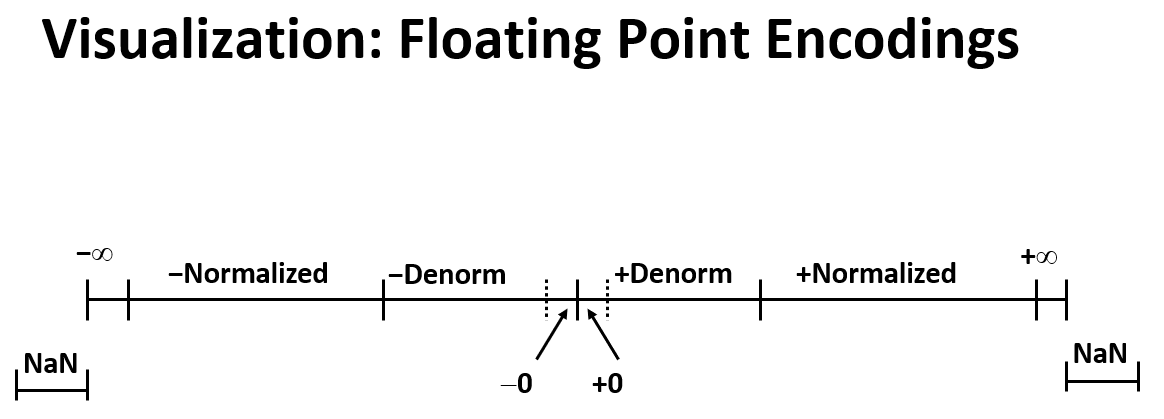
例子：
假设一个浮点数exp 是4个bits,frac 是3个bits
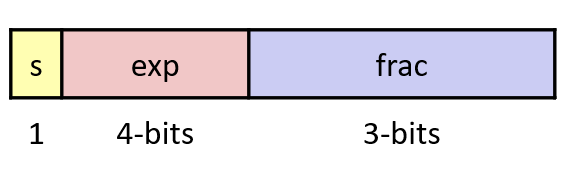
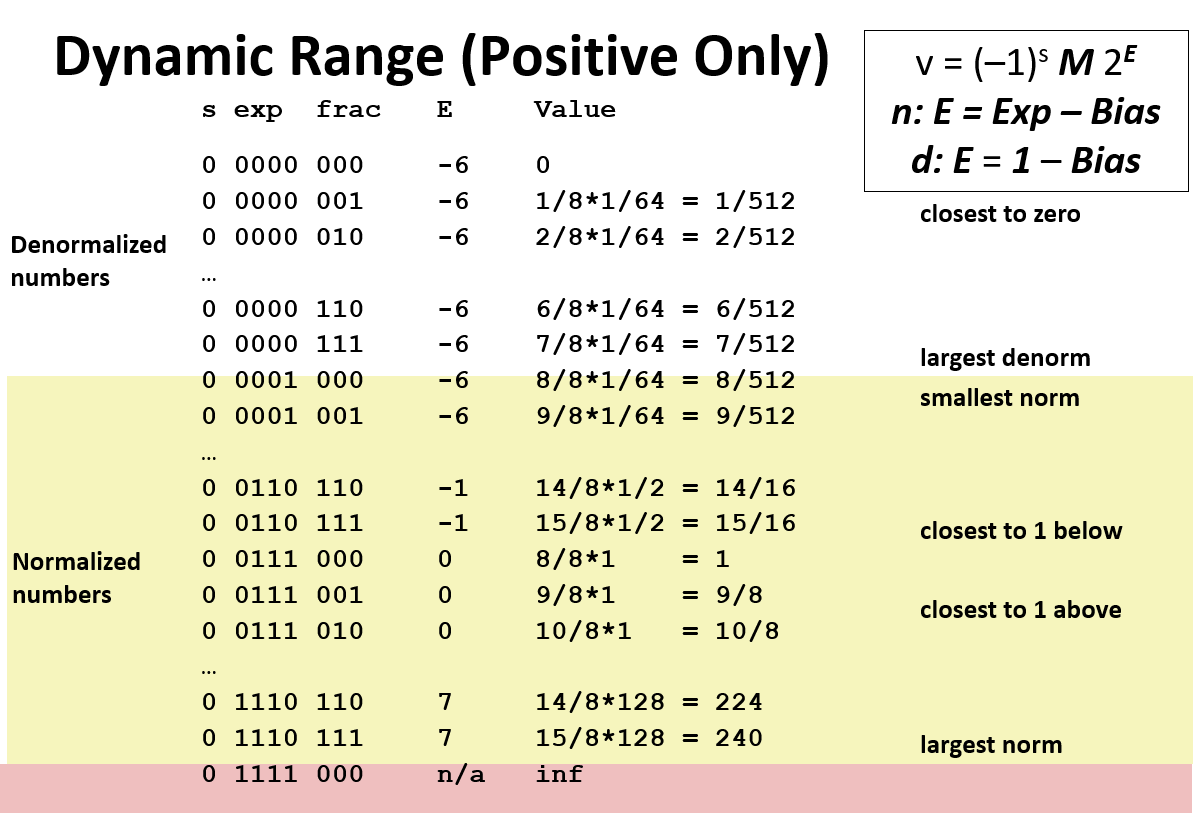
画图来表示：
假设exp 3bit ,frac 2 bit
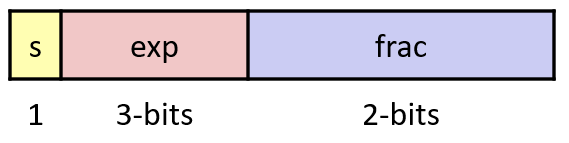
完整范围：
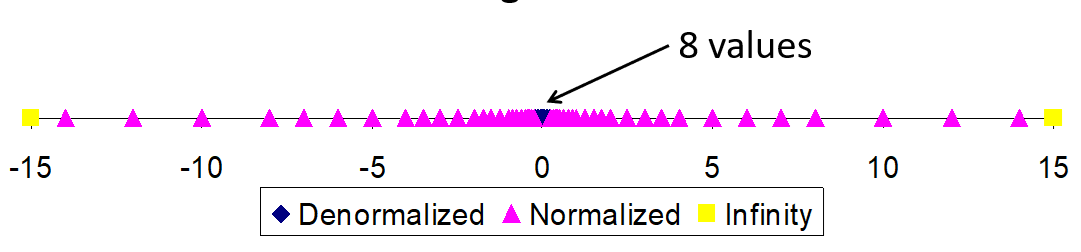
-1 ~ 1 附近的视图放大后如下：
IEEE Encoding 的特殊性质：
- 浮点0 被编码为了整数0
- All bits = 0
- 除了NaN之外，可以比较所有的浮点数，具体方法是通过将其视为无符号的整数
- Must first compare sign bits （必须首先比较最高位）
- Must consider -0 = 0 （必须考虑 -0 = 0 ）
舍入：
IEEE 有四种舍入模式：
最后一种模式是：4舍6入，5取偶
二进制数字的舍入：
浮点数乘法：
两个符号位的操作就是异或的操作，可见只有相同的时候，异或才是1 ，不一样就是0 。
两个浮点数相加：
浮点数乘法可以交换，但不具有结合性，
浮点数加法可以交换，但不具有结合性，经常发生在一个很大的数字和一个很小数字的操作上，例如3.14 和 2^10 的操作，
总结： 浮点数是不满足结合律的， 而且一般是发生在两个相差很大的数字之间的情况，所以作为程序员一定要明白数字的变化范围，重新结合或改变运算的顺序结果可能是不相同的。
现在有两种浮点数，有IEEE单精度和IEEE双精度浮点数。
Lecture03 Machine-Level Programming 01:Basics
History of Intel processors and architectures
Intel 系列的处理器俗称 x86 。 这是因为它的第一个芯片被称为8086。
然后跳过了8186，随后推出了8286，8386。
x86有时候又被称作CISC （Complex instruction set computer）。【在80年代早期有件大事，80年代又被称作RISC 和 CISC大战的年代，RISC是精简指令集计算机】
4核心芯片的构成：
8核处理器
顺便提一句的是除了 x86结构，还有ARM ，它们是两个主要的两种设计。
总结：
Intel公司，AMD公司 都是使用x86结构，
ARM 实际是 Acorn RISC Machine ，Acorn 早期是一家公司，它们在早期决定制造自己的个人电脑，它们不打算从Intel购买芯片，最后它破产了，但是它们提出了一个相当不错的指令集（Advanced RISC），非常高效简单。现在ARM是一家总部位于剑桥的公司，它出售设计而不是芯片。
C,assembly,machine code
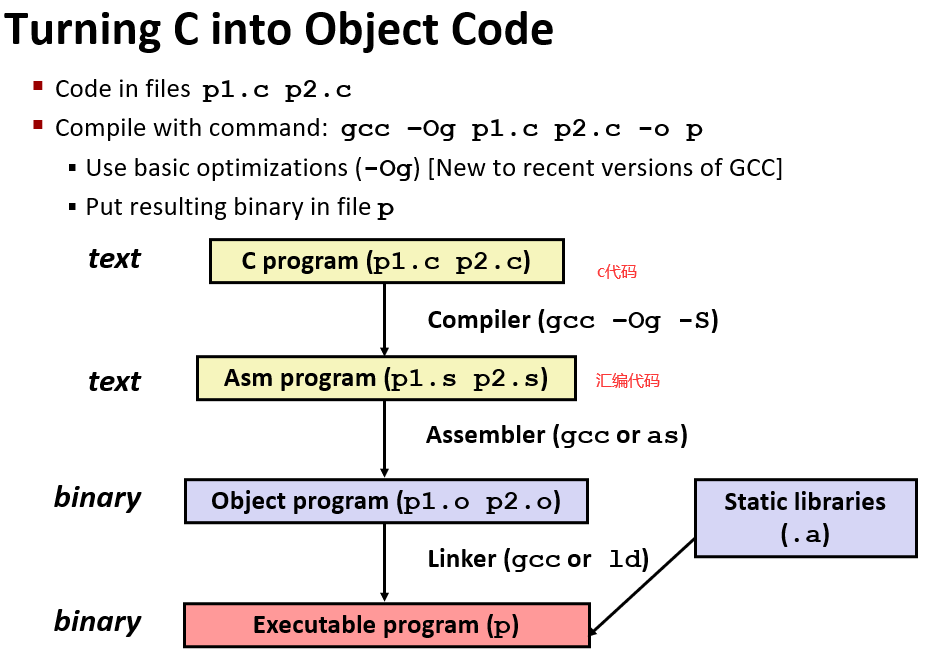
Assembly Basic:Registers,operands,move
16个寄存器，可以用来保存整数和指针。%r 代表的是64位， %e代表的是32位。
movq 指令
q of movq is quad ,意思是4个字节，64位。
注： 出于 对硬件设计者的方便，不允许从Mem 复制到 Mem, 而且Imm （立即数）也不能作为Dest。
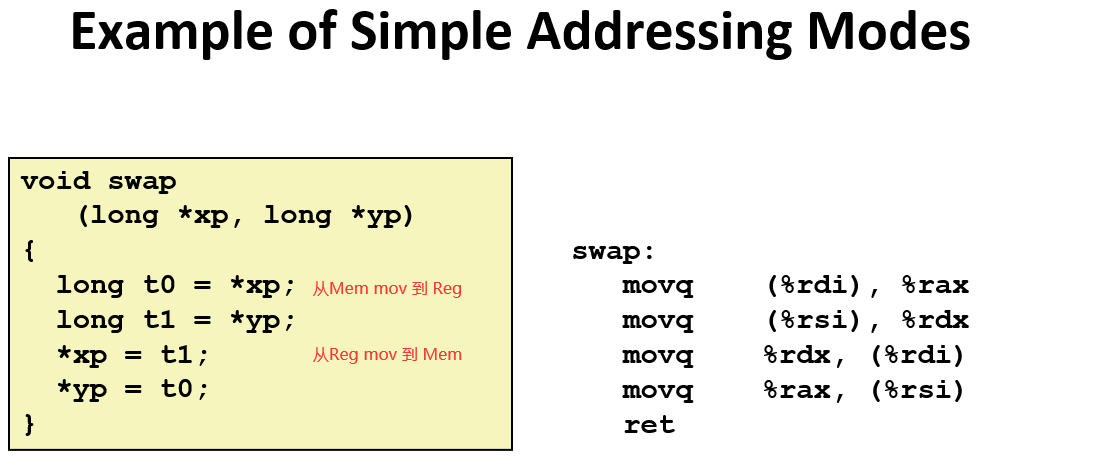
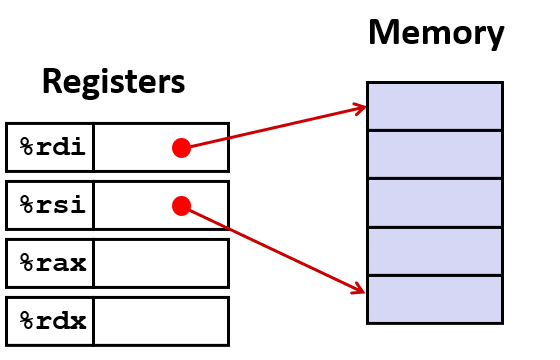
这个例子展示了非常简单的内存引用，
关于why S is 1,2,4,8, 因为如果这是一个数组索引，必须通过数据类型的字节数来缩放索引值，如果它是一个int,就必须缩放4倍，如果是long，就缩放8倍，这也是它们存在的原因。
上面是 汇编代码中内存引用的基本格式，如果不使用某些字段，可以删除其中的一些字段，如下：
Arithmetic & logical operations
lea 指令：
这里是将 3*%rdi 存储到 %rax 中，然后再讲%rax 左移2位，这也是lea 和 mov 的区别，lea 是不使用内存引用！
总之一句话，lea without memory reference, lea 常用于 整数和地址的运算~
这种做法比直接乘12 会好，因为乘法运算会很慢，
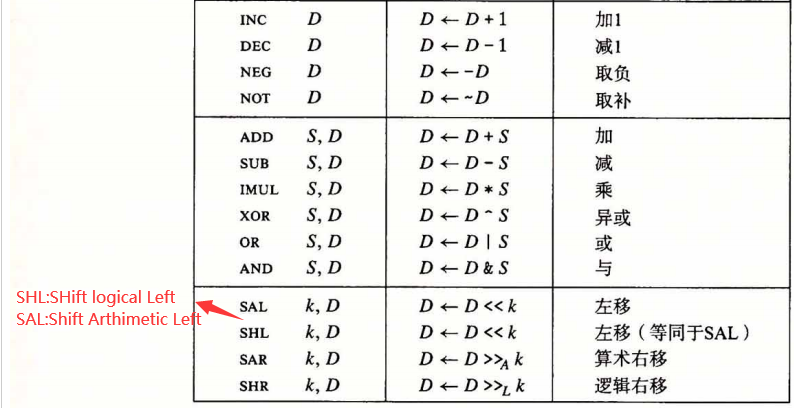
注：这里Src在前，Dest在后，
一个例子：
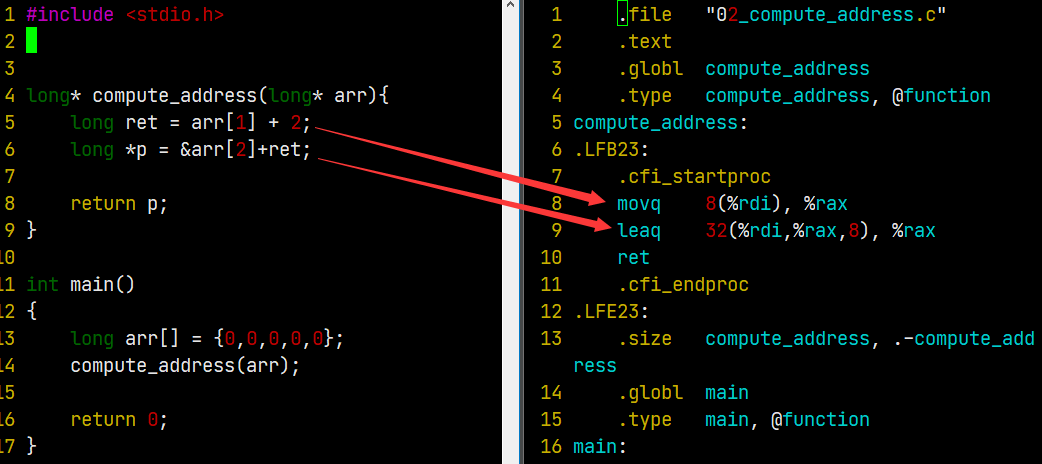
lea 的两种用法（其实是一种）：
01 Computing arithmetic expressions of the form x + k*y
#include <stdio.h> long m12(long x){ return x*12; } int main(){ return 0; }
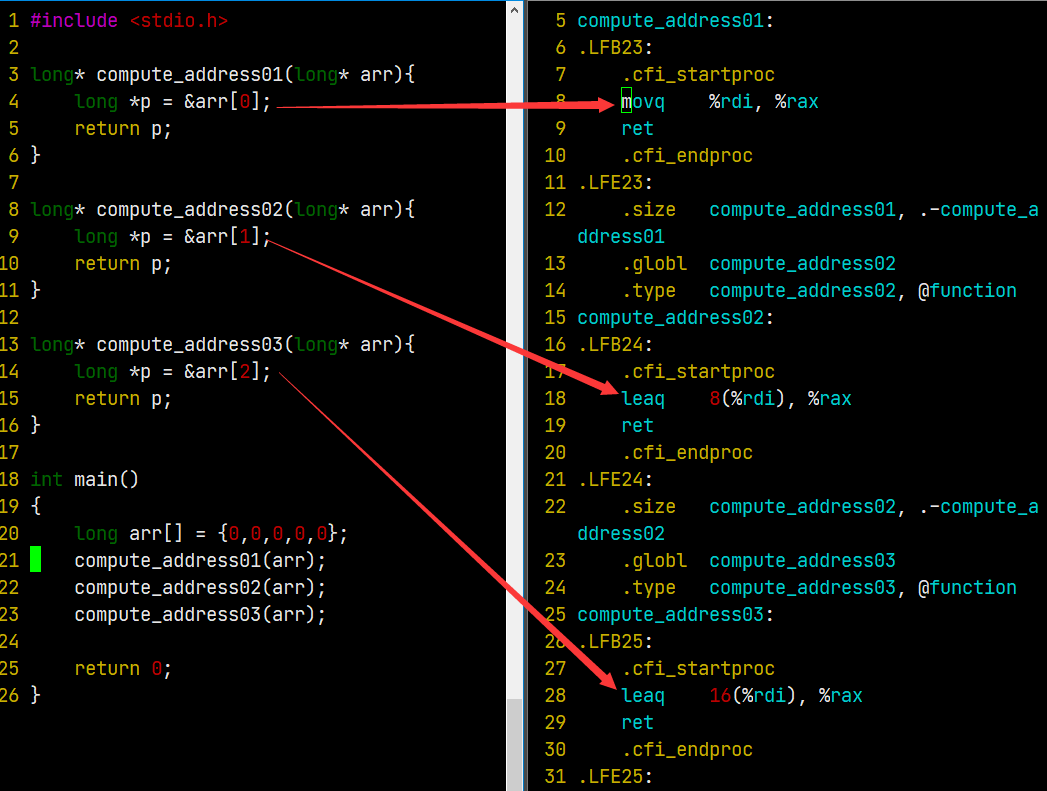
02 Computing addresses
#include <stdio.h> long* compute_address01(long* arr){ long *p = &arr[0]; return p; } long* compute_address02(long* arr){ long *p = &arr[1]; return p; } long* compute_address03(long* arr){ long *p = &arr[2]; return p; } int main() { long arr[] = {0,0,0,0,0}; compute_address01(arr); compute_address02(arr); compute_address03(arr); return 0; }
使用 gcc xxx.c -Og -S 就可以产生对应的 xxx.s 的汇编代码了。
Lecture04 Machine-Level Programming 02:Control
现在有几个问题，
寄存器（Reg） 是 内存（Mem） 的一部分？ No,
寄存器（Reg） 是缓存（Cache） 的一部分？ No,
寄存器是CPU内部用来存放数据的一些小型存储区域 。
本节主要是表述 如何控制机器级别指令的执行顺序，以及如何使用这些技术来实现基本的条件语句，循环和switch 语句 等。
Control: Condition codes
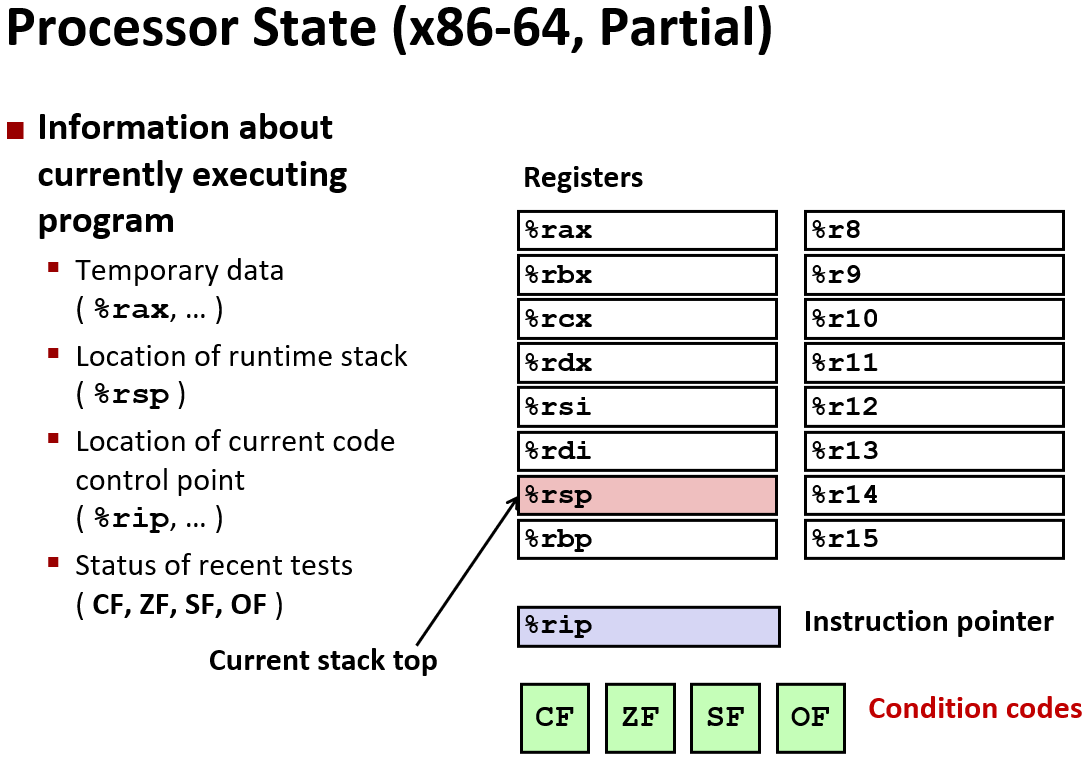
有一些指令，它们唯一的作用就是设置条件码，
这里需要提醒的是，在机器级编码中的参数顺序通常与高级语言中的顺序相反，例如：cmpq Src2,Src1, 我们在高级语言中一般是 cmp Src1,Src2。
test 指令的唯一目的也是设置条件标志，
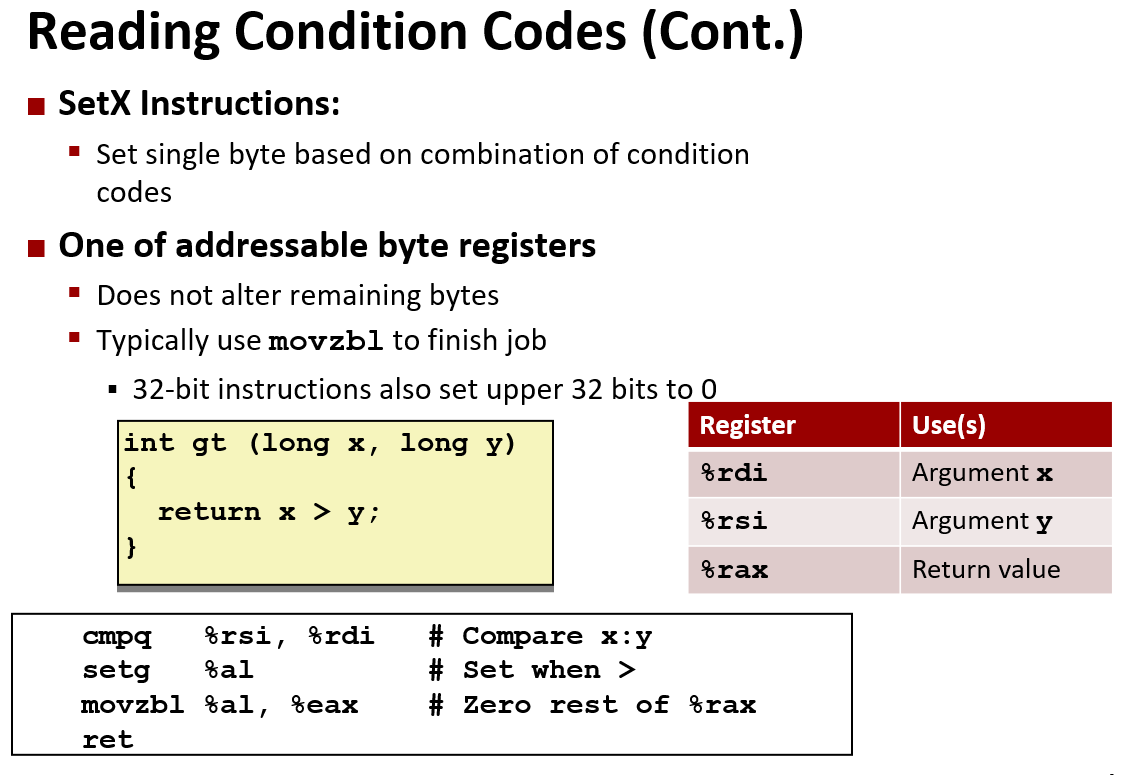
movzbl 指令，是从%al 扩展到 %eax ，eax 虽然是只有32位，但是在x86的世界里，如果对低32位做了操作，那么也相当于对高32位做了操作，
Conditional branches
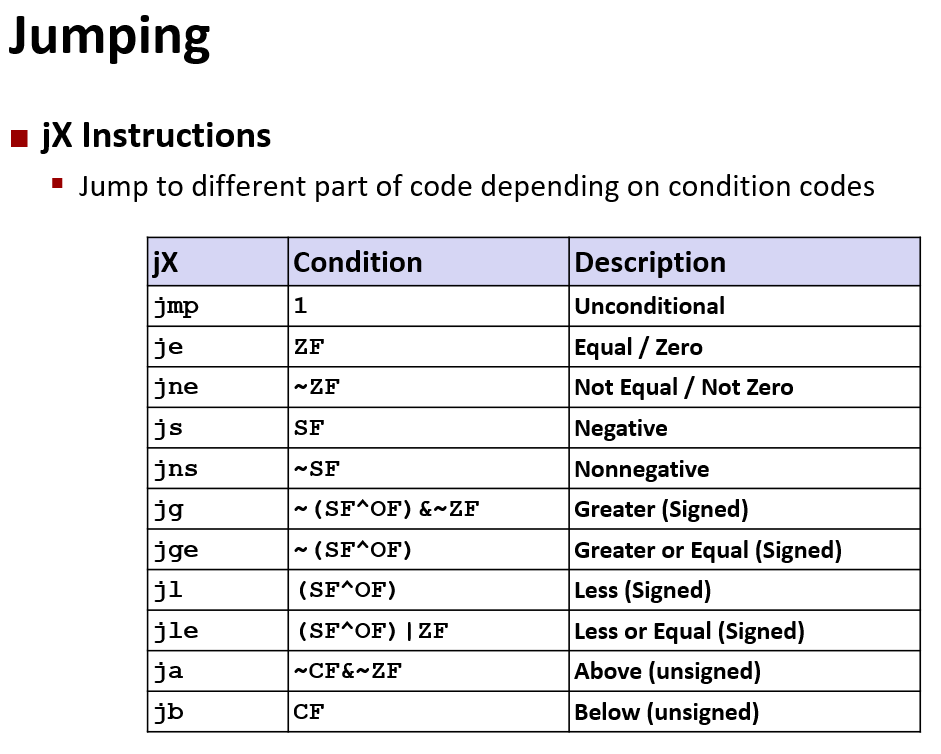
由于条件分支的汇编代码 和 C的goto 语句 很类似，由因为汇编代码可读性较差，所以下面都是用goto 形式来表述 条件分支的汇编代码。 注：（C中不建议使用goto语句）
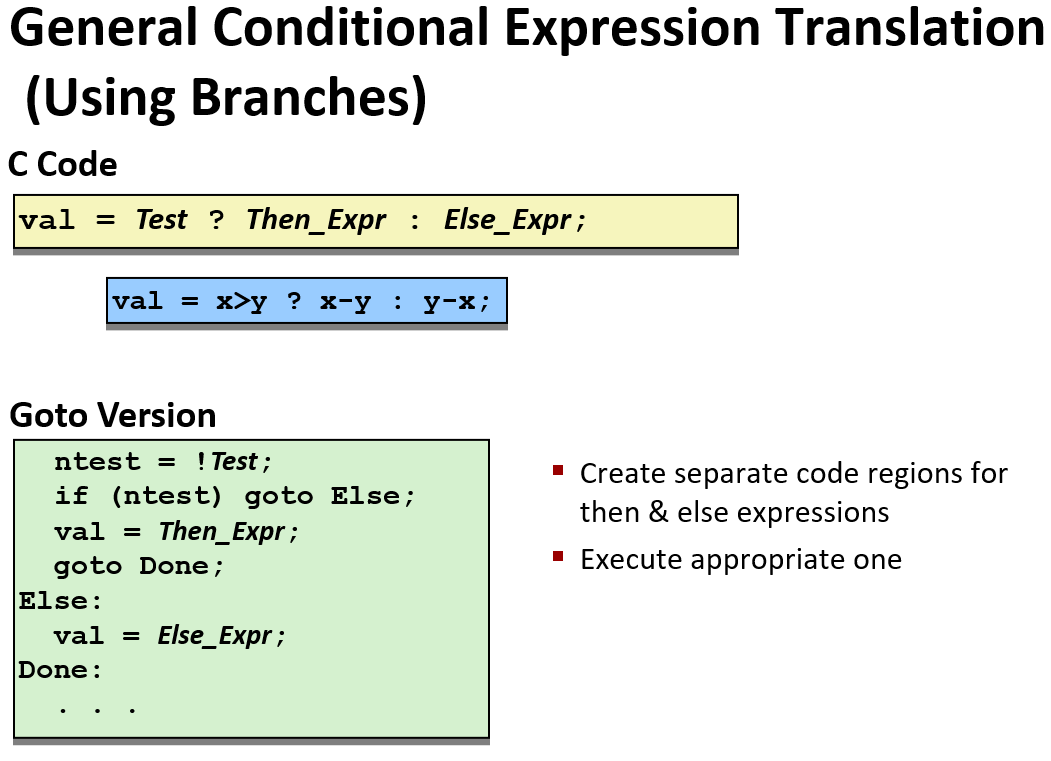
为什么不能一直使用Conditional Move?
1,进行两种情况的计算可能是一个非常非常糟糕的主意，
2，有时候确实不能这样做，例如要保证p非空指针，
3， 执行程序会影响其他分支的结果 ，例如第三种情况
Loops
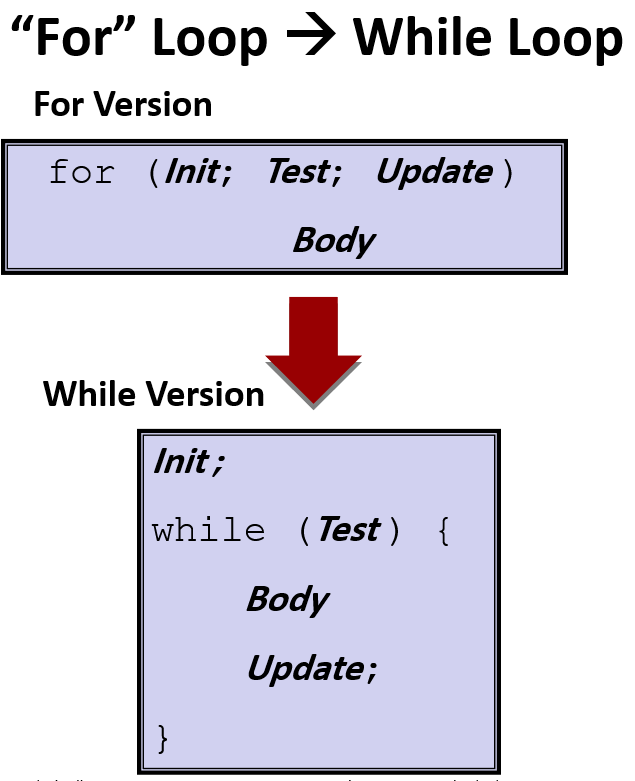
两种方式，生成While 循环的汇编代码：
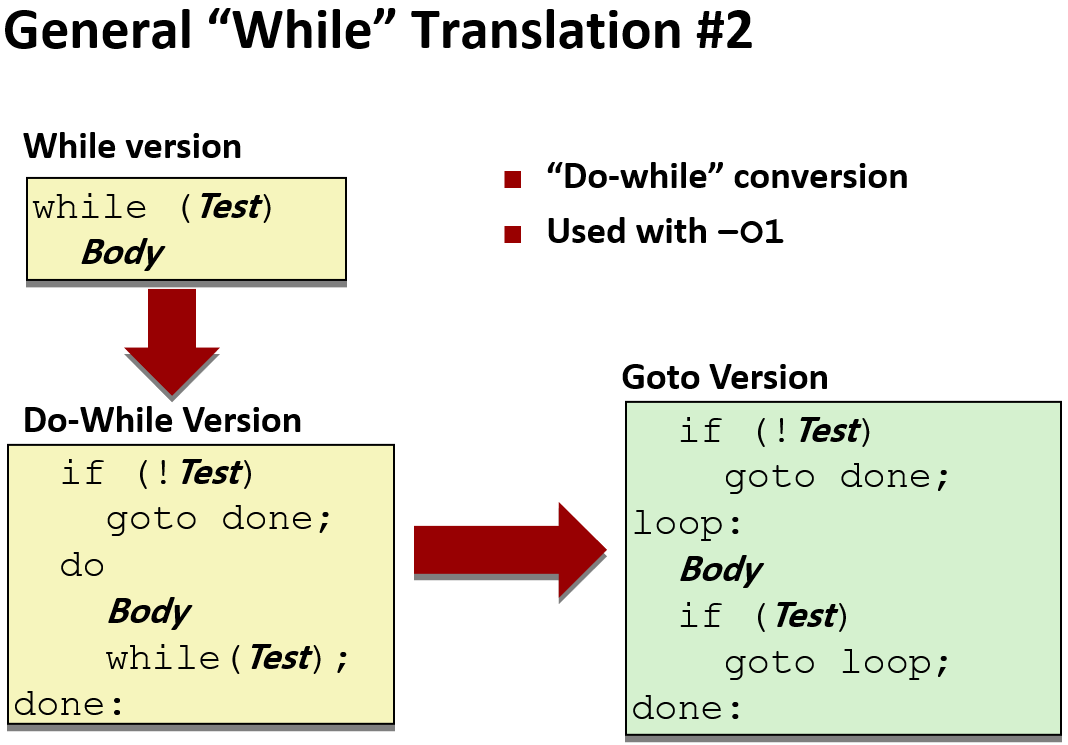
第三种循环时for 循环：
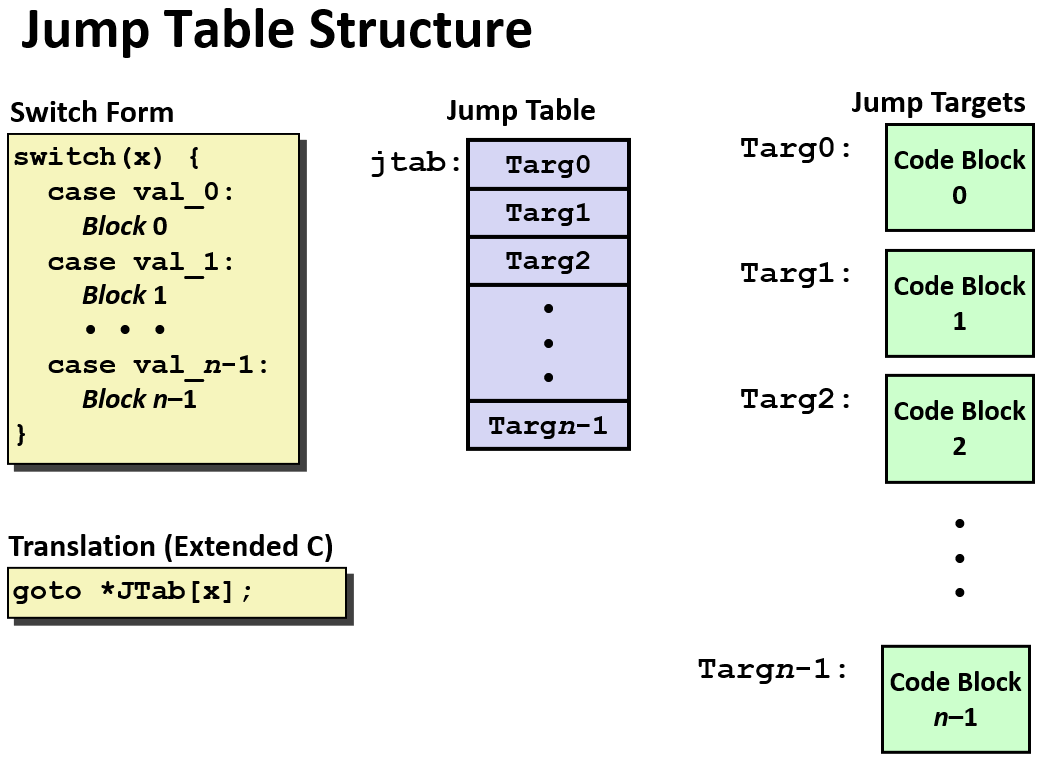
Switch Statements
switch 语句的汇编形式，
switch 的简单用法：
我们知道可以用if-else 代替 switch,所以，你可能觉得switch 的汇编代码也是 if-else 类似的汇编代码，实际上不是的！
注： ja : Jump above ,这里使用ja 而不是使用jg（jump greater），是因为如果x是负数，进行无符号的比较也会变为很大的正数。 总之，如果x 大于6，或者小于0都会直接跳到 default！
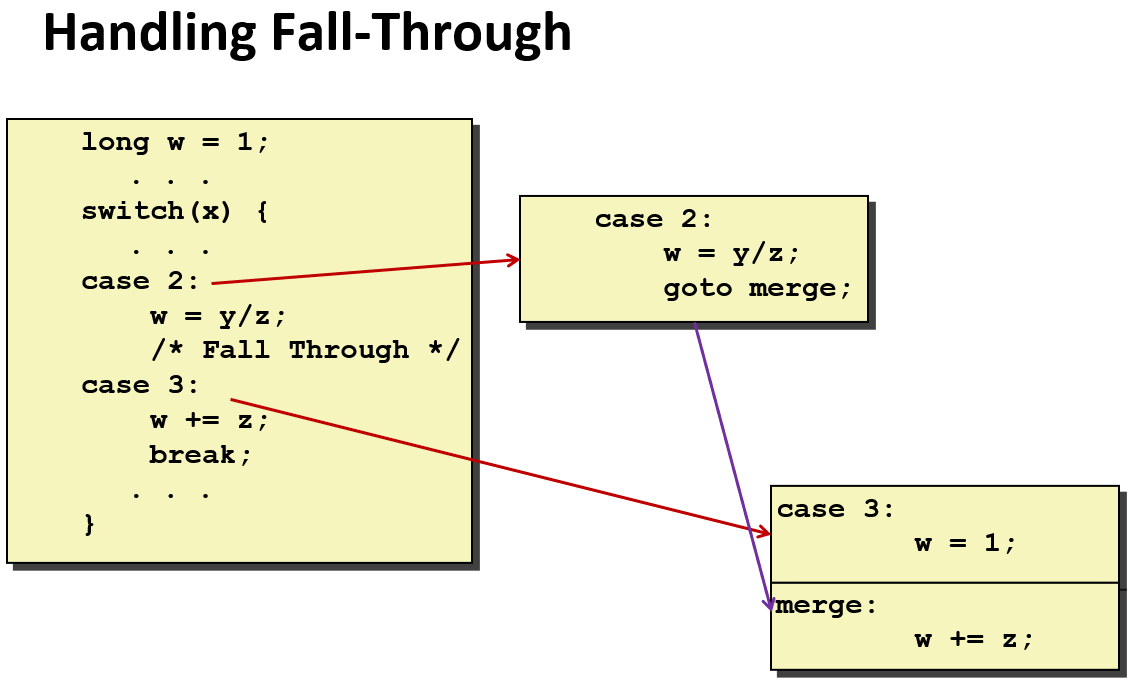
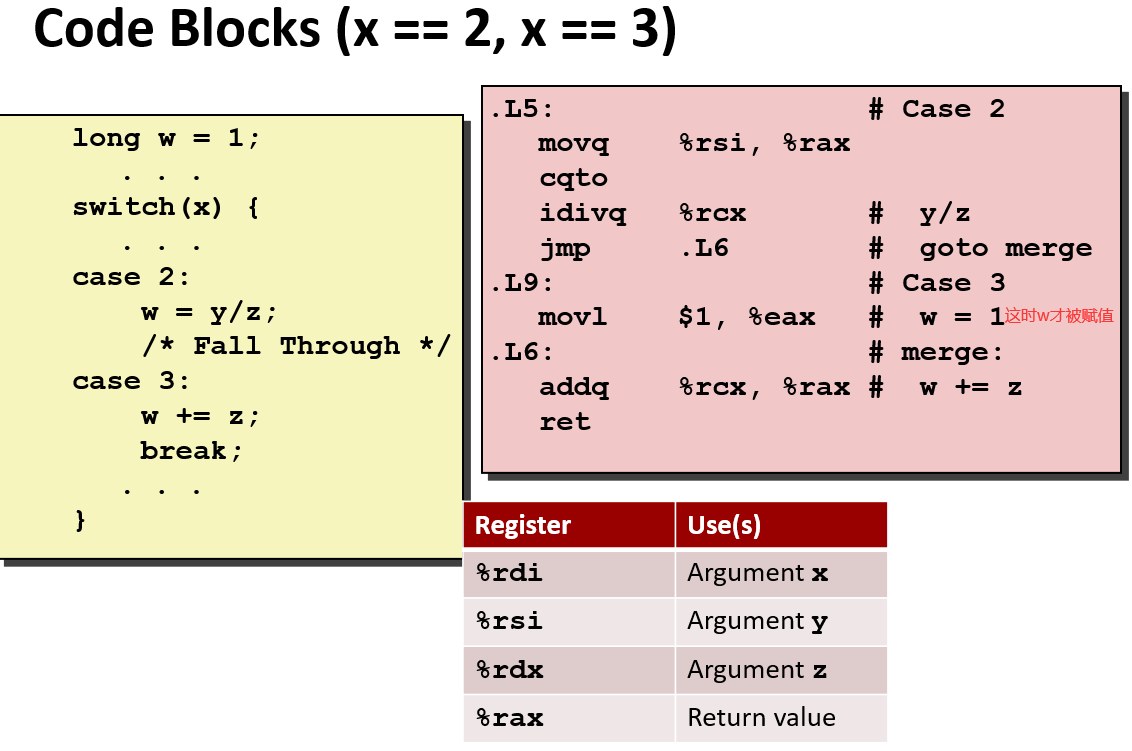
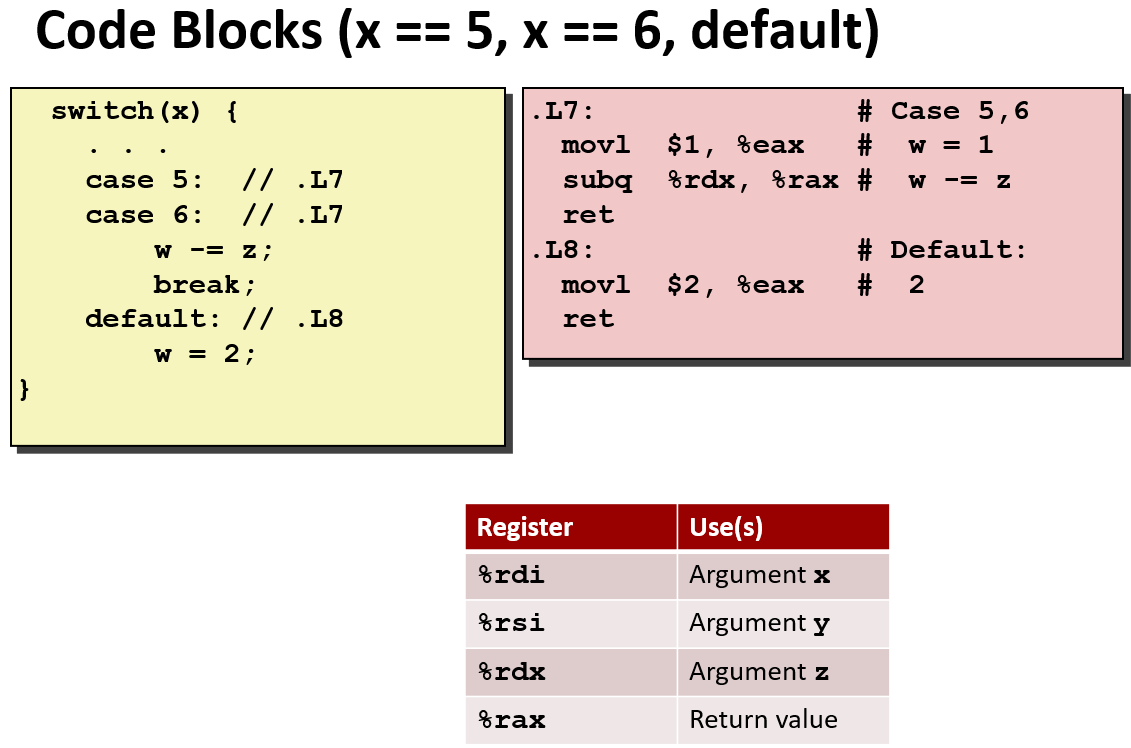
问题：
如果x是负数，通常会加上一个偏置Bias 变为正数
如果只有两个case ,case 0 和 case 10000 ,难道要建立 10000个项的表吗？ 的确是的，所以编译器会优化成为if-else 的汇编代码形式，
虽然有时switch用到不多，但是有时候也是可以带来性能的提升，因为switch表是O(1) 的时间复杂度，if-else 是线性的复杂度O(n） ，
而且，如果case是稀疏的话，它会设置一个条件树，进行二分搜索，可以达到时间复杂度为： O(logn)的级别。
不管哪种都是优于if -else 的，
总结：
基本上有三个条件控制，
1，使用条件跳转到代码的不同位置
2，是使用Condition moves (先把所有情况都计算出来，再决定跳到哪个)
3, 是使用Jump table
