01玩转数据结构_05_链表和递归

链表回顾：

leetcode 题目（No.203 移除链表元素）：

不使用虚拟头节点：

class Solution {
    public ListNode removeElements(ListNode head, int val) {
        //1，head.val 就是应该删除的节点
//        if(head != null && head.val == val ){
        while(head != null && head.val == val ){ //之所以使用while是因为可能有多个。
            ListNode delNode = head;
            head = delNode.next;
            delNode.next = null;
        }
        //2，head.val 不是应该删除的节点
        if(head ==null){
            return null;
        }
        ListNode prePtr = head;   //删除时应该要知道前一个节点。
        while (prePtr.next != null){
            if(prePtr.next.val == val){
                ListNode delNode = prePtr.next;
                prePtr.next = delNode.next;
                delNode.next = null;
            }else{
                prePtr = prePtr.next;
            }
        }
        return head;
    }
}

使用虚拟头节点：

class Solution {
    public ListNode removeElements(ListNode head, int val) {
        //使用虚拟头节点  将代码处理逻辑统一。
        ListNode dummyNode = new ListNode(0);
        dummyNode.next = head;  
        ListNode prePtr = dummyNode;
        while(prePtr.next != null){
            if(prePtr.next.val == val){
                ListNode delNode = prePtr.next; 
                prePtr.next = delNode.next; 
                delNode.next = null;     
            }else{
                prePtr = prePtr.next;  
            }
        }
        return dummyNode.next;  
        
     
    }
}

链表和递归：

递归是一个很重要的概念，它甚至是 初级程序员和高级程序员 拉开距离的分水岭。

递归基础和递归的宏观语意：

它的本质：

将原来的问题，转化为更小的同一问题！

下面我们用递归来实现一下 数组求和。

package cn.zcb.demo01;

public class MySum {
    public static void main(String[] args) {
        int [] arr = {1,2,3,4,5,6,7,8,9,10};
        int ret = sum(arr);
        System.out.println(ret);

    }
    public static int sum(int []arr){
        //为用户设计
        return sum(arr,0); // 初始索引是0 
    }
    private static int sum(int []arr,int leftIdx){
        //真正的递归函数，它额外需要一个左边界的索引 。
        //终止条件
        if(leftIdx == arr.length ){
            return 0;
        }
        //递归链条
        return arr[leftIdx] + sum(arr,leftIdx+1);
    }
}

上面递归分两处：

1，终止条件。终止条件一般比较简单，

2，递归链条。一般难的是下面的递归链表的创建（即 把原问题 转化成更小的问题）。

其实有的时候，我们不必关系递归的具体每一步骤，

而仅仅知道 该函数是干嘛的就行了（即递归函数的宏观语意）。然后，围绕它来构建终止条件  和 递归链条。  

总结：宏观语意很重要，可以直接将 函数中调用自身的函数当做是已经解决的函数。

链表的天然递归结构：

 所以，对于链表来说 ，绝大多数都是可以通过递归来进行解决的。

下面使用递归来解决上面的LeetCode题目。

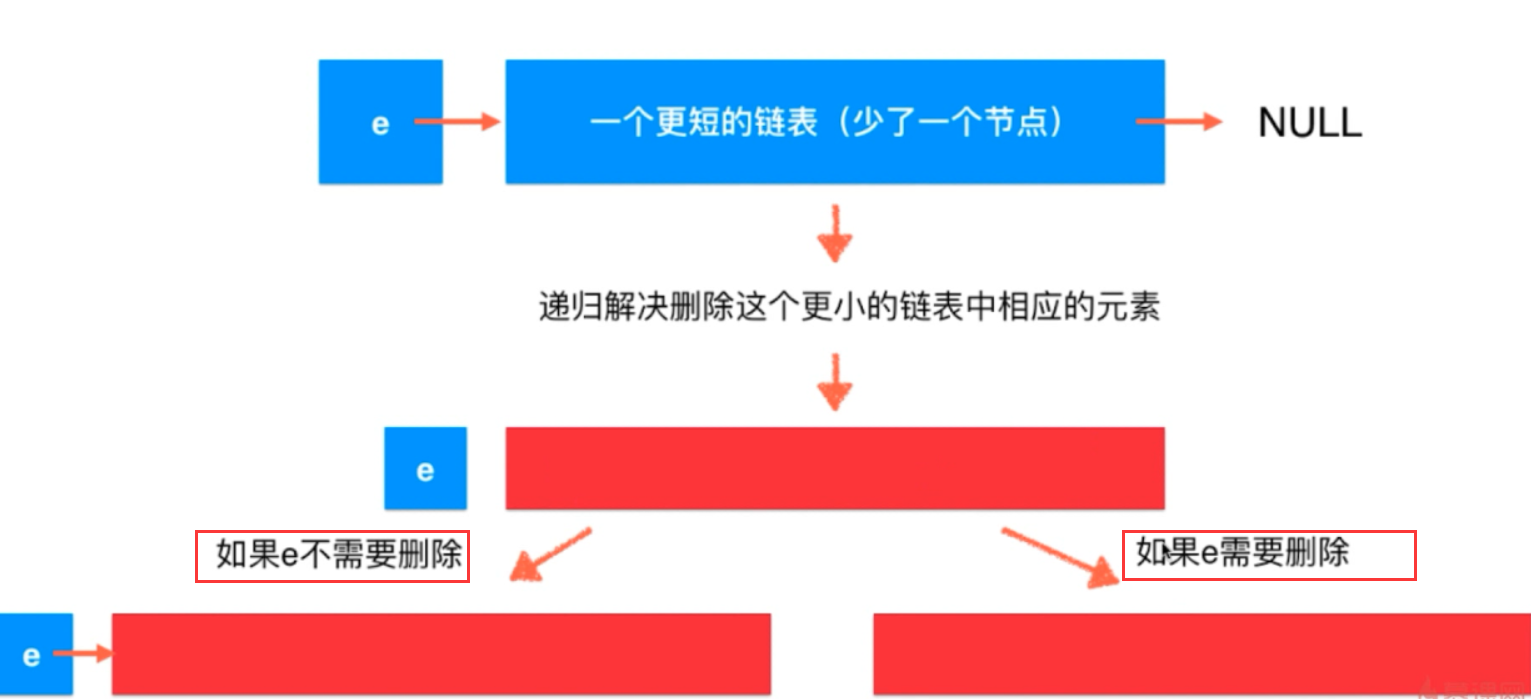
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        //终止条件
        if(head == null)
            return null;
        
        //递归链条 
        ListNode res = removeElements(head.next,val);  //假设 res 是已经清理好的链表。
        if(head.val == val){ //如果head 需要清理 直接返回 res
            return res;  
        }else{
            head.next = res;
            return head; 
        }
    }
}

package cn.zcb.demo01;
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        //终止条件
        if(head == null)
            return null;

        //递归链条
        head.next  = removeElements(head.next,val); //假设函数的返回值是 已经清理好的链表。
        if(head.val == val){ //如果head 需要清理 直接返回head.next   
            return head.next;
        }else{
            return head;
        }
    }
}

package cn.zcb.demo01;
class Solution {
    public ListNode removeElements(ListNode head, int val) {
        //终止条件
        if(head == null)
            return null;

        //递归链条
        head.next  = removeElements(head.next,val); //假设函数的返回值是 已经清理好的链表。
        return head.val == val?head.next:head;  
    }
}

递归运行的机制：递归的“微观”解读：

就解决问题本身而言，我们只需要掌握 “宏观”语意，基本上问题都能解决。 

下面我们也看下微观发生了什么！

另一题：

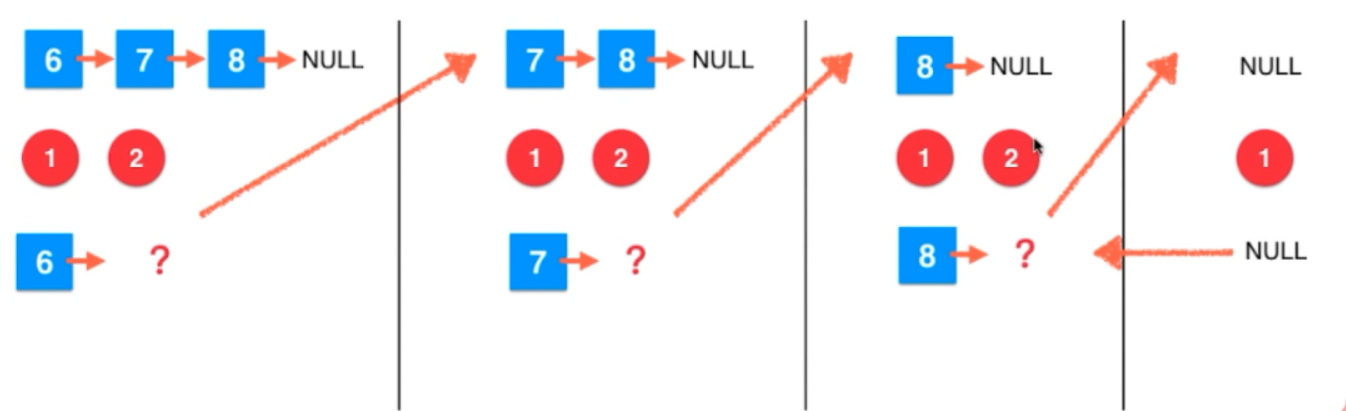
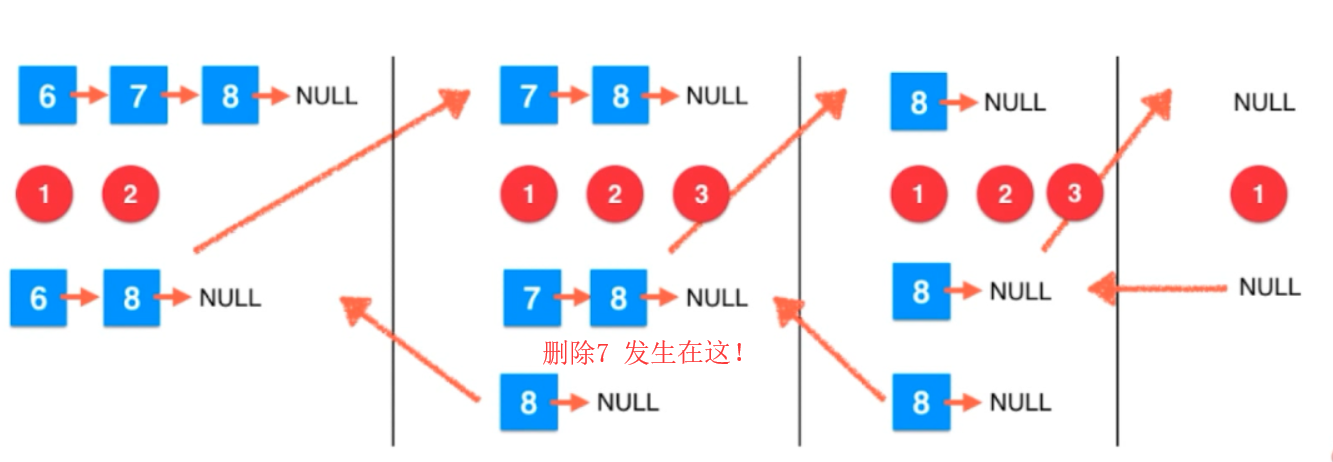
递归的代价：

对于线性结构来说，我们是可以直接使用循环来解决的。所以，我们不能发现递归的很多好处。

但是对于非线性结构（树啊，图啊之类的）来说，我们就会发现递归的好处。它的书写逻辑是清晰的。而且是简单的。

递归算法的调试（程序中调试）：

上面是在图纸上写的。对于平时写程序来说，如果每个都写在纸上也挺浪费时间，虽然它的学习效果是最好的。

其实，我们是完全可以通过打印输出进行递归调试 的 。

package cn.zcb.demo01;
class Solution {
    public ListNode removeElements(ListNode head, int val,int depth) { //depth 是递归的深度
        //终止条件
        //1,一进来就输出个 关于深度的信息。 这里用- 表示， - 表示一个深度。
        String depthString = generateDepthString(depth); //专门用来生成深度信息的函数
        System.out.print(depthString);
        System.out.println("Call: remove " + val + " in "+head);

        if(head == null) {
            //2, 结束递归时候的输出。
            System.out.print(depthString);
            System.out.println("0Return: "+head);
            return null;
        }
        //递归链条
        ListNode res = removeElements(head.next,val,depth+1);
        //3 处理完小问题之后输出一下。
        System.out.print(depthString);
        System.out.println("After remove "+val +": "+res);

        ListNode ret;
        if(head.val == val){
            ret = res;
        }else{
            head.next = res;
            ret = head;
        }
        System.out.print(depthString);
        System.out.println("1Return: "+ret);
        return ret;
    }
    private String generateDepthString(int depth){
        StringBuilder builder = new StringBuilder();
        for (int i=0;i<depth;i++){
            builder.append("-");
        }
        return builder.toString();


    }
    public static void main(String[] args) {
        int [] nums = {1,2,6,3,4,5,6};
        ListNode head = new ListNode(nums);
        System.out.println(head);

        //构建链表完毕，下面为测试 removeElements() 代码
        ListNode res =  (new Solution()).removeElements(head,6,0);
        System.out.println(res);
    }

}

package cn.zcb.demo01;

public class ListNode {
    public int val;
    public ListNode next;
    public ListNode(int val){
        this.val = val;
    }
    //int [] 数组作为参数的构造器
    public ListNode(int [] arr){
        if(arr == null || arr.length ==0 ){
            throw new IllegalArgumentException("数组不能为空 ！");
        }
        this.val  = arr[0];

        ListNode temp = this;
        for (int i=1;i<arr.length;i++){
            temp.next = new ListNode(arr[i]);
            temp = temp.next;
        }
    }
    //重写toString()
    @Override
    public String toString(){
        StringBuilder builder = new StringBuilder();
        ListNode temp =this;
        while (temp != null){
            builder.append(temp.val +"->");
            temp = temp.next;
        }
        builder.append("null");
        return builder.toString();
    }
}

原本只有四行的代码，被我们整成了 这么多行， 它说明 牛逼的算法可能是需要上百上千的代码才可以透彻的理解的。才能潇洒的写出那四行代码的。

更多的 和 链表相关的话题：

链表的形态了解：

1，双链表：

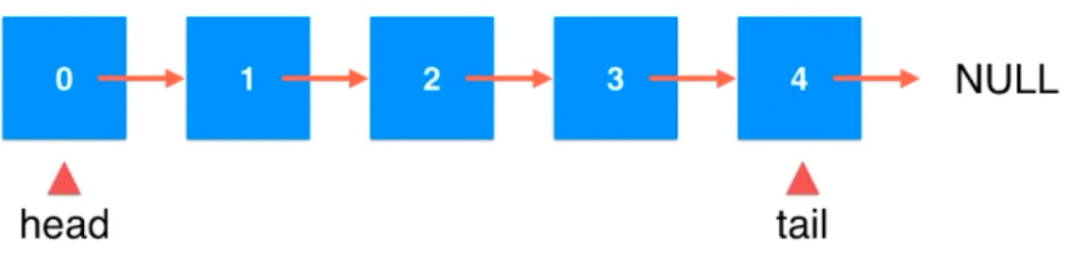
我们之前的问题，在对队列尾端删除的时候，即使有tail ，也需要O(n) 的时间复杂度。

其实，我们可以用双链表来 解决这个事情。

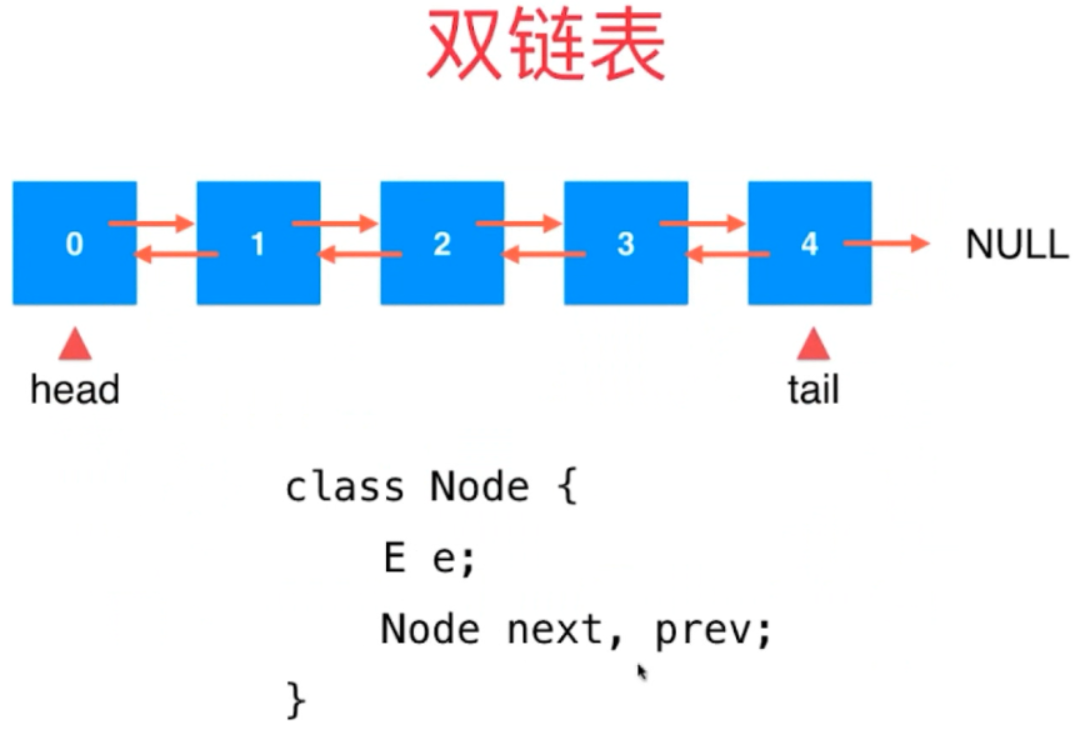
不过，这样带给我们的代价是，由于有两个指针，所以维护起来会比较麻烦。

当然，双链表也可以通过使用 虚拟头节点 去使得处理逻辑统一。

2，循环链表：

进一步，有循环链表（双向），它可避免使用tail 指针了就。

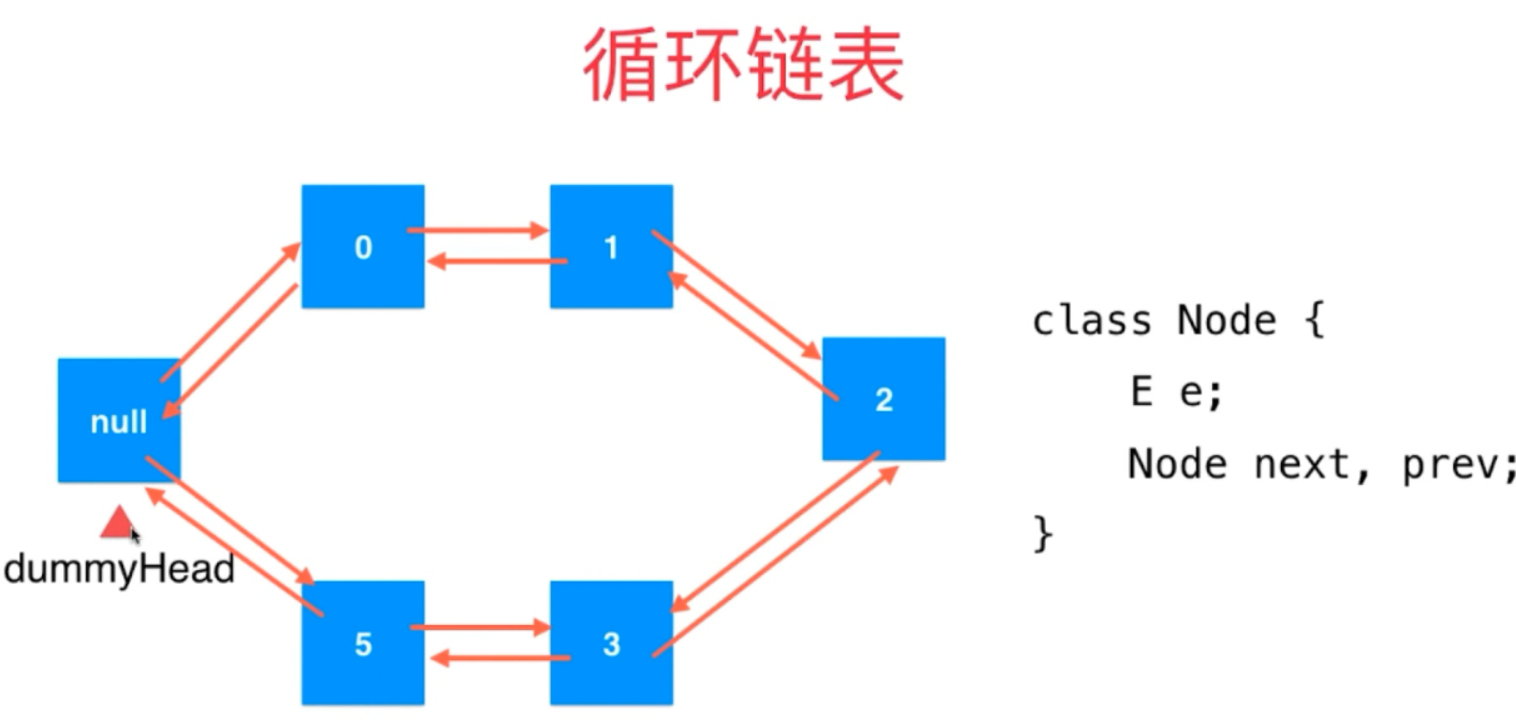
链表也可以用数组来实现：

3，数组链表：

至此，之前的内容都是关于线性的。下面将进入非线性。首先的就是二分搜索树。