第一章:行列式
简单行列式:


三阶行列式:

n 阶行列式:


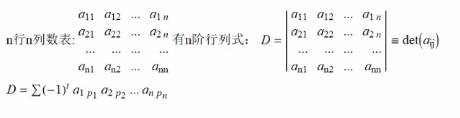
行列式的性质:
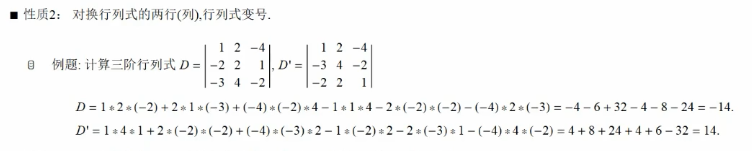




行列式的降阶(按行/按列展开):



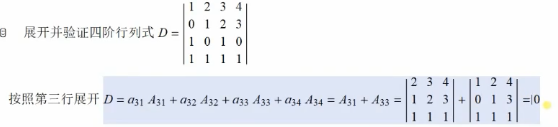

1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 5 if 0: 6 d = np.array([ 7 [4, 1, 2, 4], 8 [1, 2, 0, 2], 9 [10, 5, 2, 0], 10 [0, 1, 1, 7] 11 ]) 12 print(d) 13 print(np.linalg.det(d)) 14 pass 15 16 if 1: 17 # 练习2 18 def createD(a, x, n): 19 # 构建函数,生成一个n阶的行列式,其中对角线值为x,其余为a 20 d = np.eye(n) 21 d = d * x 22 d[d == 0] = a 23 return d 24 25 26 d = createD(5, 20, 10) 27 print(d) 28 print(np.linalg.det(d)) 29 pass
第二章:矩阵


矩阵的运算:



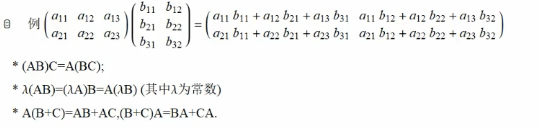
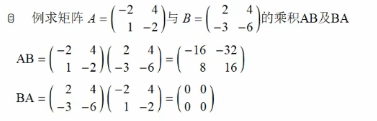


逆矩阵:

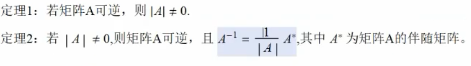
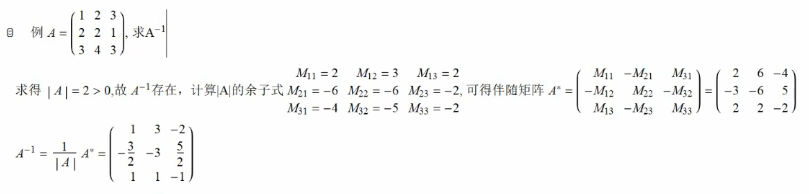



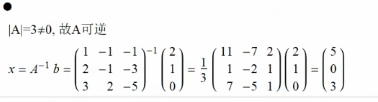

1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 5 #构造矩阵 6 if 0: 7 d = np.arange(50).reshape(10,5) 8 # print(d) 9 10 d2 = np.eye(10)*10 11 # print(d2) 12 13 d3 = np.arange(10).reshape((10,1)) #列向量 14 # print(d3) 15 16 pass 17 18 #矩阵的运算 19 if 0: 20 d1 = np.arange(12).reshape(3,4) 21 d2 = np.arange(10,22).reshape((3,4)) 22 # print(d1) 23 # print(d2) 24 d3 = np.ones((3,4)) 25 d4 = np.ones((3,5)) 26 # print(d3) 27 # print(d4) 28 29 30 #矩阵加法 (shape 需要相同) 31 # print(d1+d2) 32 33 #数字与矩阵的乘法 34 res = 10*d1 35 # print(res) 36 37 #数组乘法 38 res = d1*d2 39 # print(res) 40 41 #矩阵乘法 42 d5 = np.arange(12).reshape((3,4)) 43 d6 = np.arange(10,22).reshape((4,3)) 44 res = np.dot(d5,d6) #dot product 点积 45 # print(res) 46 47 #矩阵的转置 48 res = d5.T 49 # print(res) 50 51 #逆矩阵 52 d6 = np.arange(1,10).reshape((3,3)) 53 d6[0][0] = 0 54 print(d6) 55 res = np.linalg.inv(d6) #inv 可以求出逆矩阵 56 print(res) 57 pass
第三章:矩阵变换与线性方程组:
矩阵变换:





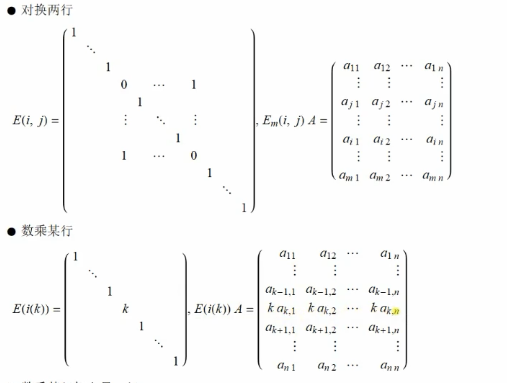



线性方程组:






1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 5 #计算秩 6 if 0: 7 a = np.array([ 8 [1, 2, 3], 9 [2, 3, -5], 10 [4, 7, 1] 11 ]) 12 b = np.array([ 13 [3, 2, 0, 5, 0], 14 [3, -2, 3, 6, -1], 15 [2, 0, 1, 5, -3], 16 [1, 6, -4, -1, 4] 17 ]) 18 res1 = np.linalg.matrix_rank(a) 19 res2 = np.linalg.matrix_rank(b) 20 # print(res1,res2) 21 pass 22 23 #计算有多少个解 24 if 0: 25 a = np.array([ 26 [1, 2, 2, 3], 27 [2, 1, -2, -2], 28 [1, -2, -4, -3] 29 ]) 30 ab = np.array([ 31 [1, 2, 2, 3, 0], 32 [2, 1, -2, -2, 0], 33 [1, -2, -4, -3, 0] 34 ]) 35 n = 4 36 ra = np.linalg.matrix_rank(a) 37 rab = np.linalg.matrix_rank(ab) 38 39 print(n, ra, rab) #n= 4 ra = 3 rb =3 此时有 无穷多个解 40 pass 41 42 if 1: 43 a = np.array([ 44 [4, 2, -1], 45 [3, -1, 2], 46 [11, 3, 0] 47 ]) 48 ab = np.array([ 49 [4, 2, -1, 2], 50 [3, -1, 2, 10], 51 [11, 3, 0, 8] 52 ]) 53 n = 4 54 ra = np.linalg.matrix_rank(a) 55 rab = np.linalg.matrix_rank(ab) 56 57 print(n, ra, rab) # 4 2 3 ra != rb 因此无解 58 pass
第四章:向量,矩阵及其对角化:







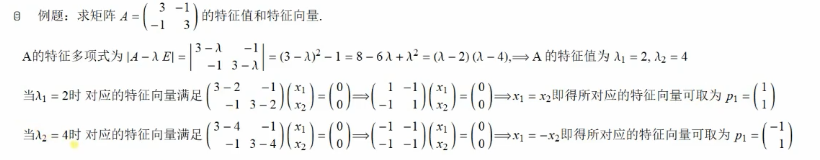




1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 5 #计算方阵的特征值 np.linalg.eigvals() 6 #np.linalg.eig() → 返回包含特征值和对应特征向量的元组 7 if 0: 8 a = np.array([ 9 [3, -1], 10 [-1, 3] 11 ]) 12 print(np.linalg.eigvals(a)) 13 print(np.linalg.eig(a)) 14 pass 15 16 17 #方阵的对角化 np.diag() → 对角化 18 if 0: 19 a = np.array([ 20 [-2, 1, 1], 21 [0, 2, 0], 22 [-4, 1, 3] 23 ]) 24 #特征值 25 vals = np.linalg.eigvals(a) 26 #对角化矩阵 27 print(np.diag(vals)) 28 pass

