一:第一章:
基本初等函数:

1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 5 import warnings 6 warnings.filterwarnings('ignore') #不发出警告 7 8 #映射与函数 9 #幂函数 10 if 0: 11 x = np.linspace(-np.pi,2*np.pi,num = 50) 12 y = x**2 13 14 plt.scatter(x,y,marker='.') 15 plt.plot(x,y) 16 17 #辅助线 18 plt.axvline(0,color ='cyan',linestyle = '--',alpha = 0.8) 19 plt.axhline(0,color='cyan',linestyle='--',alpha = 0.8) 20 21 22 plt.show() 23 pass 24 #指数函数 25 if 0: 26 x = np.linspace(-np.pi,2*np.pi,num = 50) 27 y = 2**x #指数函数 28 29 plt.scatter(x,y,marker='.') 30 plt.plot(x,y) 31 32 plt.axhline(0,color='cyan',linestyle='--',alpha = 0.8) 33 plt.axvline(0,color='cyan',linestyle='--',alpha = 0.8) 34 35 plt.show() 36 pass 37 38 #对数函数 39 if 0: 40 x = np.linspace(-np.pi,2*np.pi,num= 50) 41 y = np.log2(x) 42 43 plt.scatter(x,y,marker = '.') 44 plt.plot(x,y) 45 46 plt.axhline(0,color='cyan',linestyle = '--',alpha = 0.8) 47 plt.axvline(0,color='cyan',linestyle = '--',alpha = 0.8) 48 49 plt.show() 50 51 52 53 pass 54 55 #三角函数 56 if 0: 57 x = np.linspace(-np.pi,2*np.pi,num=50) 58 y = np.sin(x) 59 60 plt.scatter(x,y,marker ='.') 61 plt.plot(x,y) 62 63 plt.axhline(0,color = 'cyan',linestyle ='--',alpha = 0.8) 64 plt.axvline(0,color='cyan',linestyle = '--',alpha = 0.8) 65 66 plt.show() 67 68 pass 69 70 #反三角函数 71 if 0: 72 #f = arcsin(x) 73 x = np.linspace(-np.pi,2*np.pi,num = 100) 74 y = np.arccos(x) 75 76 plt.scatter(x,y,marker = '.') 77 plt.plot(x,y) 78 79 plt.axhline(0,color='cyan',linestyle='--',alpha = 0.8) 80 plt.axvline(0,color='cyan',linestyle='--',alpha = 0.8) 81 82 plt.show() 83 pass
数列 和函数的极限:

1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 5 # import warnings 6 # warnings.filterwarnings('ignore') #不发出警告 7 8 #数列 x/(x+1) 的极限 9 if 0: 10 x = np.arange(50) 11 y = x/(x+1) 12 13 plt.scatter(x,y,marker = '.') 14 plt.plot(x,y) 15 16 plt.axvline(0,color='cyan',linestyle='--',alpha = 0.8) 17 plt.axhline(0,color='cyan',linestyle='--',alpha = 0.8) 18 19 plt.show() 20 21 pass 22 23 #函数的极限 24 if 0: 25 x = np.linspace(-2,2,num=100) 26 y = x**2 -1 27 28 plt.scatter(x,y,marker = '.') 29 plt.plot(x,y) 30 31 plt.axvline(0,color='cyan',linestyle='--') 32 plt.axhline(0,color='cyan',linestyle='--') 33 34 #极限值 35 plt.axhline(-1,color='red',linestyle = '--') 36 plt.show() 37 pass 38 39 40 #练习 :极限 41 #函数的极限 42 if 1: 43 x = np.arange(1,50) 44 y = (2*x+1)/x 45 46 plt.scatter(x,y,marker = '.') 47 plt.plot(x,y) 48 49 # plt.axhline(2) #默认颜色是类似于 cyan 50 plt.axhline(2,color='red') #默认是直线 51 52 53 plt.show() 54 pass
二:第二章:
导数与微分:

1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 5 #导数 6 if 0: 7 def f(x): 8 return x**2 9 10 plt.figure(figsize = (12,6)) 11 n = np.linspace(-10,10,num=50) 12 13 plt.plot(n,f(n)) 14 plt.xlim(-10,10) 15 # plt.ylim(-10,100) #设置axes 的limits 16 17 #画出两点一线 18 plt.plot([2,5],[4,25],color='r') 19 20 x_m = 2 21 for i in range(1,5): 22 plt.plot([x_m,x_m+i],[f(x_m),f(x_m+i)],color='r') 23 24 25 26 27 28 29 30 plt.show() 31 32 pass 33 34 #求函数在一点处的导数 35 if 0: 36 def f(x): 37 return x ** 2 38 def ds(x,d): 39 ''' 40 41 :param x: 选取一点 42 :param d: 向右偏离x 的距离 43 :return: 斜率 44 ''' 45 y1 = f(x) 46 y2 = f(x+d) 47 return (y2-y1)/d 48 49 for i in np.linspace(1,0,num=1000,endpoint=False): #endpoint 可以控制是否要右端点 50 ret = ds(2,i) #求 在 f(x)=x^2 当x = 10 时的导数 51 print("当2 偏{:.3f} 个单位的时候,直线的斜率是{:.3f}".format(i,ret) ) 52 pass 53 #图示 54 if 0: 55 def f(x): 56 return x**2 57 n = np.linspace(-10,10,num = 50) 58 plt.plot(n,f(n)) 59 60 plt.scatter(2,4) 61 plt.plot(n,4*n-4) 62 63 plt.show() 64 65 pass 66 67 68 # 69 if 0: 70 def f_(x): 71 return 1 - 10 * x + 6 * x ** 2 - (1 + x ** 2) / (2 * x ** 2) + 3 * np.cos(x) * x + 3 * np.sin(x) 72 73 def f(x): 74 return 2*x**3 -5*x**2 + 3*x*np.sin(x) + (x**2 +1)/(2*x) -7 75 76 x = np.linspace(10,0,num=100,endpoint=False) 77 plt.figure(figsize=(12,6)) 78 plt.plot(x,f(x)) 79 80 m= n = 6 81 plt.scatter(m,f(m)) 82 83 plt.plot(x,f_(x)) 84 plt.show() 85 pass
泰勒公式:


导数与微分的应用:
单调性和凸凹性
单调性判断:f'(x) >0 增 反之减
凸凹形 :f''(x) >0 凹 反之 凸
方程的近似解
二分法:

切线法:




1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 5 #函数的单调性和 曲线的凸凹性 6 if 0: 7 def f1(x): 8 return 2*x**3 - 9*x**2 +12*x -3 9 10 x =np.linspace(-10,10,num= 100) 11 plt.plot(x,f1(x)) 12 13 #辅助线 14 plt.axvline(0,color = 'gray',linestyle='--',alpha =0.8) 15 plt.axhline(0,color = 'gray',linestyle='--',alpha =0.8) 16 17 18 19 plt.show() 20 pass 21 22 #二分法求解 23 if 0: 24 def f(x): 25 return x**3 + 1.1*x**2 +0.9*x -1.4 26 x = np.linspace(-10,10,num=100) 27 plt.plot(x,f(x)) 28 29 plt.axvline(0,color='cyan',linestyle='--') 30 plt.axhline(0,color='cyan',linestyle='--') 31 #二分法 32 33 res_ls=[0,1] 34 for i in range(10): 35 mid = (res_ls[0] +res_ls[1])/2 36 if f(mid)*f(0) < 0: 37 res_ls[1] = mid 38 else: 39 res_ls[0] = mid 40 print("第{} 次循环,此时的区间为 {} !".format(i+1,res_ls)) 41 pass 42 43 #切线法求解 44 if 1: 45 def f(x): 46 return x**3 + 1.1*x**2 +0.9*x -1.4 47 #f(x) 在0 -1 单调递增 48 49 plt.xlim([0,1]) 50 plt.ylim([f(0),f(1)]) 51 52 x = np.linspace(0,1,num=100) 53 plt.axvline(0,color='cyan',linestyle='--') 54 plt.axhline(0,color='cyan',linestyle='--') 55 plt.plot(x,f(x)) 56 57 58 #切线法 59 res = 1 60 #f(x) 的导数 61 def f_1(x): 62 return 3*x**2 +2.2*x +0.9 63 for i in range(10): 64 p_Pre = res 65 res = res - f(res)/f_1(res) 66 print("第{}次循环的估计值为{}".format(i+1,res)) 67 plt.plot([p_Pre,res],[f(p_Pre),0]) 68 pass 69 70 plt.show()
三:第三章:不定积分,定积分
不定积分:

不定积分的方法:
换元法
分部积分法


小结:

定积分:
定积分的解法:
牛顿-莱布尼茨公式:

换元法与分部积分法:

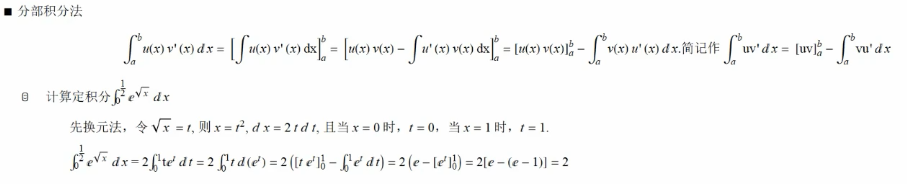
定积分的应用:
1,计算图形的面积
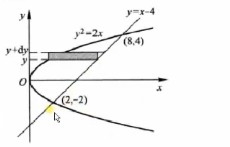
2,计算体积:

1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 5 #定积分的求解 6 if 0: 7 def f(x): 8 return x**2 9 10 x = np.linspace(-1,2) 11 plt.plot(x,f(x)) 12 plt.axhline(0,color='cyan',linestyle='--') 13 plt.axvline(0,color='cyan',linestyle='--') 14 plt.axvline(1,color='cyan',linestyle='--') 15 #填充图形 16 x1 = np.linspace(0,1) #要填充的x 17 plt.fill_between(x1,0,f(x1),color='k',alpha =0.4) #第一个参数是 要覆盖的区域,第二个是下限,第三个是上限 18 19 #上面都是在画图,下面计算 20 area =0 21 for i in range(len(x1))[:-1]: #去掉最后一个 22 mid_idx = (x1[i] +x1[i+1])/2 23 area += (x1[i+1]-x1[i])*f(mid_idx) 24 print(area) #0.3332986255726781 25 pass 26 27 #计算图形的面积: 28 if 0: 29 def f1_1(x): 30 return (2*x)**0.5 31 def f1_2(x): 32 return -(2*x)**0.5 33 34 def f2(x): 35 return x-4 36 x = np.linspace(0,10,num=100) 37 plt.plot(x,f1_1(x),'r', 38 x,f1_2(x),'g', 39 x,f2(x),'b') 40 41 plt.xlim([-2,10]) 42 plt.ylim([-6,6]) 43 #辅助线 44 plt.axvline(0,color='cyan',linestyle='--') 45 plt.axhline(-2,color='cyan',linestyle='--') 46 plt.axhline(4,color='cyan',linestyle='--') 47 #下面是计算 48 y = np.linspace(-2,4,num=100) 49 area = 0 50 for i in range(len(y))[:-1]: 51 y_midIdx = (y[i]+y[i+1])/2 52 area += (y_midIdx+4 -y_midIdx**2/2)*(y[i+1] - y[i]) 53 print(area) #18.000918273645556 54 # 真实的解 为 18 55 pass 56 57 #计算图形的面积(0-np.pi/2) 58 if 0: 59 def f(x): 60 return (x +np.sin(x)) /(1+np.cos(x)) 61 x = np.linspace(-0.8*np.pi,0.8*np.pi,num=100) 62 plt.plot(x,f(x)) 63 64 #辅助线 65 plt.axhline(0,color ='cyan',linestyle='--') 66 plt.axvline(0,color ='cyan',linestyle='--') 67 plt.axvline(np.pi/2,color ='cyan',linestyle='--') 68 69 x1 = np.linspace(0,np.pi/2,num=100) 70 plt.fill_between(x1,0,f(x1),color ='k',alpha=0.4) 71 72 #计算 73 area = 0 74 for i in range(len(x1))[:-1]: 75 mid_idx = (x1[i]+x1[i+1])/2 76 area += (x1[i+1] -x1[i])*f(mid_idx) 77 print(area) #1.5707693613636802 78 79 pass 80 81 82 plt.show()
四:第四章:多元函数与重积分
多元函数:

偏导数:

全微分:

重积分:
二重积分:
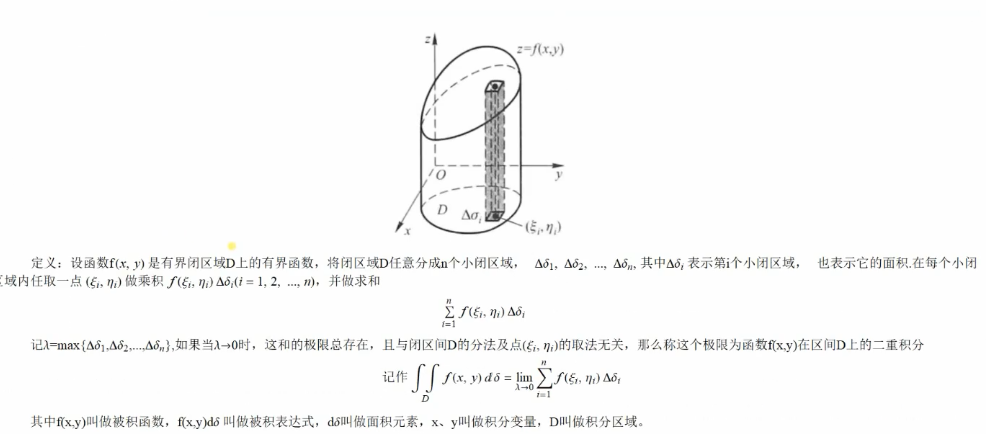
二重积分的求解:
1,直角坐标系

2,极坐标系

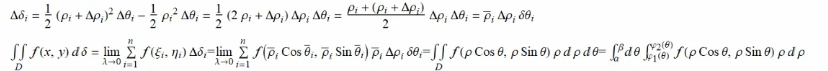

三重积分及解法:





1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 5 from mpl_toolkits.mplot3d import axes3d 6 7 #画 z = sin(x+y) 的图 8 if 1: 9 fig = plt.figure() 10 ax = fig.gca(projection='3d') 11 12 x = np.linspace(-np.pi,np.pi) 13 y = np.linspace(-np.pi,np.pi) 14 x,y = np.meshgrid(x,y) 15 z = np.sin(x+y) 16 17 18 ax.view_init(elev=30) 19 # cmap = 'Reds' 20 # cmap = 'Greens' 21 # cmap = 'Blues' 22 ax.plot_surface(x,y,z,rstride=2,cstride=2,cmap='Greens', alpha=0.9) 23 24 plt.show()

1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 5 from mpl_toolkits.mplot3d import axes3d 6 7 #画 z = sin(x+y) 的图 8 if 0: 9 fig = plt.figure() 10 ax = fig.gca(projection='3d') 11 12 x = np.linspace(-np.pi,np.pi) 13 y = np.linspace(-np.pi,np.pi) 14 x,y = np.meshgrid(x,y) 15 z = np.sin(x+y) 16 17 18 ax.view_init(elev=30) 19 # cmap = 'Reds' 20 # cmap = 'Greens' 21 # cmap = 'Blues' 22 ax.plot_surface(x,y,z,rstride=2,cstride=2,cmap='Greens', alpha=0.9) 23 24 25 #画 z = x**2 +3*x*y +y**2 区域 x【-5,5】y【-5,5】 26 if 1: 27 fig = plt.figure() 28 ax = fig.gca(projection='3d') 29 # ax.view_init(elev=None,azim=None) 30 31 x = np.linspace(-5,5) 32 y = np.linspace(-5,5) 33 x,y = np.meshgrid(x,y) 34 z = x**2 +3*x*y +y**2 35 #画线框架图 36 ax.plot_wireframe(x,y,z,rstride=2,cstride=2,color='k',alpha=0.8,linewidth=0.5) 37 38 #等高线 contour 是登高的意思 39 ax.contourf(x, y, z, zdir='z', offset=-40, cmap='Blues', alpha=0.7) 40 ax.contourf(x, y, z, zdir='x', offset=-6, cmap='Blues', alpha=0.7) 41 ax.contourf(x, y, z, zdir='y', offset=6, cmap='Blues', alpha=0.7) 42 43 ax.scatter(1, 2, 11, s=20, c='k') 44 # 曲面上的点(1,2,11) 45 46 def fxz(x): 47 return 2 ** x + 6 48 49 50 xn1 = np.linspace(1, 2, num=20) 51 yn1 = np.ones_like(xn1) * 2 52 zn1 = fxz(xn1) 53 ax.plot(xn1, yn1, zn1, '-r') 54 55 56 # 将y看成常量,则y=2,也就是在y=2这个面上,xz组成的函数求导 57 def fyz(y): 58 return 2 ** y + 3 59 60 61 yn2 = np.linspace(2, 3, num=20) 62 xn2 = np.ones_like(xn1) * 1 63 zn2 = fyz(yn2) 64 ax.plot(xn2, yn2, zn2, '-b') 65 # 将x看成常量,则x=1,也就是在x=1这个面上,yz组成的函数求导 66 pass 67 plt.show()

1 import numpy as np 2 import pandas as pd 3 import matplotlib.pyplot as plt 4 5 from mpl_toolkits.mplot3d import axes3d 6 7 #画 z = sin(x+y) 的图 8 if 0: 9 fig = plt.figure() 10 ax = fig.gca(projection='3d') 11 12 x = np.linspace(-np.pi,np.pi) 13 y = np.linspace(-np.pi,np.pi) 14 x,y = np.meshgrid(x,y) 15 z = np.sin(x+y) 16 17 18 ax.view_init(elev=30) 19 # cmap = 'Reds' 20 # cmap = 'Greens' 21 # cmap = 'Blues' 22 ax.plot_surface(x,y,z,rstride=2,cstride=2,cmap='Greens', alpha=0.9) 23 24 #画 z = x**2 +3*x*y +y**2 区域 x【-5,5】y【-5,5】 25 if 0: 26 fig = plt.figure() 27 ax = fig.gca(projection='3d') 28 # ax.view_init(elev=None,azim=None) 29 30 x = np.linspace(-5,5) 31 y = np.linspace(-5,5) 32 x,y = np.meshgrid(x,y) 33 z = x**2 +3*x*y +y**2 34 #画线框架图 35 ax.plot_wireframe(x,y,z,rstride=2,cstride=2,color='k',alpha=0.8,linewidth=0.5) 36 37 #等高线 contour 是登高的意思 38 ax.contourf(x, y, z, zdir='z', offset=-40, cmap='Blues', alpha=0.7) 39 ax.contourf(x, y, z, zdir='x', offset=-6, cmap='Blues', alpha=0.7) 40 ax.contourf(x, y, z, zdir='y', offset=6, cmap='Blues', alpha=0.7) 41 42 ax.scatter(1, 2, 11, s=20, c='k') 43 # 曲面上的点(1,2,11) 44 45 def fxz(x): 46 return 2 ** x + 6 47 48 49 xn1 = np.linspace(1, 2, num=20) 50 yn1 = np.ones_like(xn1) * 2 51 zn1 = fxz(xn1) 52 ax.plot(xn1, yn1, zn1, '-r') 53 54 55 # 将y看成常量,则y=2,也就是在y=2这个面上,xz组成的函数求导 56 def fyz(y): 57 return 2 ** y + 3 58 59 60 yn2 = np.linspace(2, 3, num=20) 61 xn2 = np.ones_like(xn1) * 1 62 zn2 = fyz(yn2) 63 ax.plot(xn2, yn2, zn2, '-b') 64 # 将x看成常量,则x=1,也就是在x=1这个面上,yz组成的函数求导 65 pass 66 plt.show()
